Chapter 19 Electric Charge and Electric Field

任何活动产生的净电荷量为零. The net amount of electric charge produced in any process is zero.

电荷从一个物体转移到另一个物体.

经典的两个例子:

毛皮和橡胶棒摩擦, 通常毛皮会失去电子, 橡胶棒带负电
丝绸和玻璃棒摩擦, 通常丝绸会失去电子, 玻璃棒带负电

失去电子的原因似乎是摩擦产生热量, 进而激发电子离开.

19.2 Electric Charge in the Atom

为什么摩擦后的物体在一段时间后又恢复到了电中性?

由于水分子的极性, 也就是说尽管水分子是呈中性, 但是其内部的电荷分布不均衡, 因此物体上的电荷会被水分子上偏正电性的一端所吸引, 就会 leak off into air.

19.3 Insulators and Conductors

Insulating 就是 ‘绝缘的’ 的意思.

绝缘体并不是完全不导电. 其难导电的原因是由于其内部电子在原子间的运动受到阻碍. 其电阻极大, 导致它的表面不允许电子流动.

Insulating material 中的电子 bound very tightly to th nuclei.

19.5 Coulomb’s Law

公式为:

$F = k \frac{Q_1Q_2}{r^2}$

k 是一个常量. $k = 8.988 \times 10^9 N \cdot m^2/C^2$

一个电子 electron 的电荷量为:

$e = 1.602 \times 10^{-19}C$

e 被定义为一个正值. 因此 electron 的电荷量实际为 -e.

任何物体的净电荷都必须是 e 的整数倍如: e, 2e, 3e …

k 常用另一个常量 $\epsilon_0$ 替换 (其为空间的介电常数):
$$
k = \frac{1}{4 \pi \epsilon_0}, \epsilon_0 = 8.85 \times 10^{-12}C^2/N \cdot m^2
$$
因此, Coulomb’s Law 又被写成:
$$
F = \frac{1}{4 \pi \epsilon_0} \frac{Q_1 Q_2}{r^2}
$$

19.6 The Electric Field

电场的大小和 test charge 的电荷量无关, 因为这里的 test charge 取的电荷量是极小的, 不会影响到电场, 也可以通过库仑定理推出. (也就是说一个电荷也能产生电场, 此时这个电场是和周围的电势差决定的)

电场被定义为, 作用在一个极小的正电荷上的力除以这个电荷的电荷量:
$$
E = \frac{F}{q}
$$
方向为电荷受到的力的方向. 单位是 N\C .

另一个常用的形式为:
$$
E = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r^2}
$$
(这里也可以看到电场大小和测试电荷无关, 这里的 Q 同样是产生电场的电荷的电荷量, 电场的方向也取决于产生电场的电荷的电性)

可以想, 电场力的大小和距离有关, 这里自然也是. 隔得近, 受到的电场力大, 电场也大.

如果一个场内有多个电荷, 那么总电场就是所有电场的叠加.

19.7 Electric Field Calculations for Continuous Charge Distributions

形成电场的这个物体, 我们一般可以看作是电荷均匀分布的, 用微分的方式写为 $dQ$. 电场就是:
$$
dE = \frac{1}{4 \pi \epsilon_0} \frac{dQ}{r^2}
$$
总的电场就是:
$$
E = \int dE
$$
$dE$ 是一个矢量.
(也就是说一个物体表面附有电子, 且均匀分布)

模型题

注意给出了电荷密度的, 也需要在最后将电荷密度表示出来, 如:

单位长度的电荷密度, 为 $\frac{Q}{L}$
单位面积的电荷密度, 为 $\frac{Q}{C}$
单位体积的电荷密度, 为 $\frac{Q}{V}$

Uniformly charged ring

电荷在圆环上均匀分布, 已知单位长度的电荷密度 $\lambda$, 求轴线上的电场大小.

先求 $dQ$ 形成的电场, 再求积分.

经验:

利用对称性减轻计算的复杂程度
用 charge density 来表示 $dQ$
对 r 的范围作出判断

A line of charge

先求一小段 $dy$ 形成的电场, 再求积分

Uniformly charged disk

已知的是电荷密度 $\sigma$ 单位是 $C/m^2$.

先算出圆环形成的电场, 再通过积分.

这里得到的一个结论为, 如果圆盘的半径特别大, 无穷大, 那么:
$$
E = \frac{\sigma}{2 \epsilon_0}
$$

A plane of charge

两个 plates 之间的距离 d 非常小. 用上面的结论.
$$
E = \frac{\sigma}{2 \epsilon_0}
$$

内部为两倍, 外部为零.

19.8 Field Lines

电场线的方向为 positive test charge 的受力方向.

也就是说, 一个带电物体产生的电场作用于外面一个 positive test charge, 这个 charge 受力的方向就是电场线的方向.

电场线的密集程度可以反映电场的大小.

电场线不会相交.

19.9 电场和导体 Electric Field and Conductors

导体内部的电场始终为零, (只是电场为零, 并不代表导体内部没有电荷, 导体内部存在大量电荷) 不论是实心还是空心, 若内部的一侧带电, 那么电子会移动到相对的一侧并将其抵消.

导体的电性都是表现在表面. any net charge on a conductors distributes itself on the surface.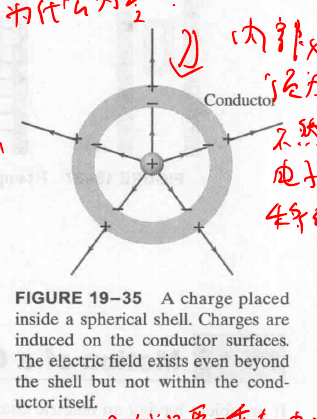

如果导体内部此时有一个大电场, 其内部的大量可移动电荷就会形成另一个电场将其抵消.

当一个导体处于一个电场中时, 如: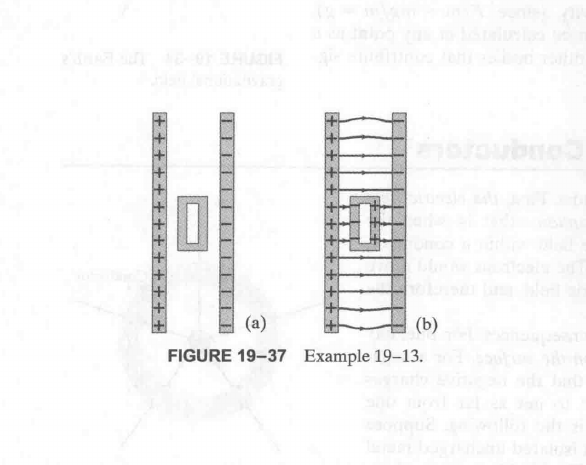

这个导体表现出来的是电场为零, 因为内部形成的电场会和外部的抵消.

19.10 带电粒子在电场中的移动 Motion of Charged Particle in an Electric Field

还是高中的那一套: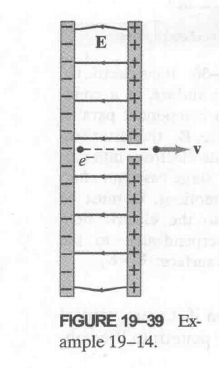

$$
F = qE, \newline
a = \frac{F}{m} = \frac{qE}{m}, \newline
v = \sqrt{2ax}
$$

19.11 Electric Dipoles

Electric Dipoles 是大小相等, 电性相反, 之间有一段距离 l 的两个带电粒子.

$Ql$ 被称作 dipole moment, 用符号 p 表示, 是一个矢量 (毕竟是 moment).

含有 electric dipole 的分子如 CO 被称作 polar molecules.

Dipole in an External Field

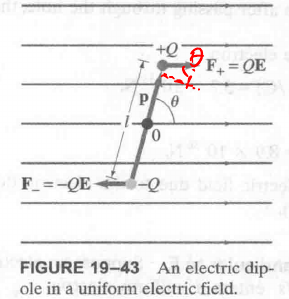
电场分布均匀, 这里 dipole 受到的合外力就为 0. 但是有 torque 作用在上面:
$$
\tau = QE \frac{l}{2} sin\theta + QE \frac{l}{2} sin\theta = pE sin\theta
$$
这里的 $pE sin\theta$ 就可以写成叉乘的形式:

$$
\tau = p \times E
$$

转动系做的功就是力矩乘以旋转的角度:

$$
W = \int_{\theta 1}^{\theta 2} \tau d\theta
$$

注意, 电偶做的功和其势能为相反数.

Chapter 20 Gauss’s Law

高斯定理是用来描述 electric charge 和 electric field 的关系的.

公式内容:
$$
\oint E \cdot dA = \frac{Q_{encl}}{\epsilon_0}
$$

高斯定理是 Coulomb’s law 的一种更 general 的形式.

20.1 Electric Flux

$\phi$ 可以看作是垂直穿过的电场线的总条数.

Electric Flux 的定义为:
$$
\phi_E = EA
$$
E 是电场强度 (可以看作是电场线的密度), A 是平面的面积. (因此可以理解为, 电场线的面密度乘以面积, 就得到了电场线的总条数)

由于是要垂直穿过, 而电场和面不一定垂直, 如: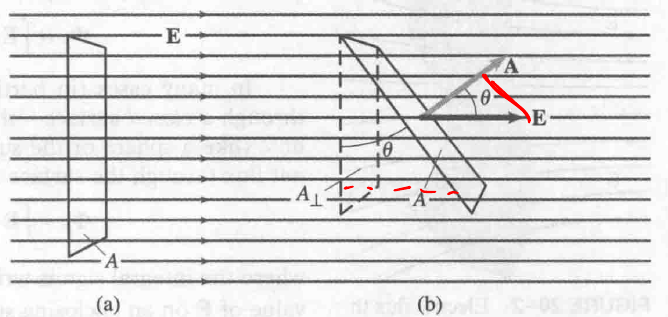

所以这样写:
$$
\phi_E = EA_T = EAcos\theta
$$
看到 $cos\theta$ 我们可以写为点乘的形式:
$$
\phi_E = E \cdot A
$$
改成点乘后要注意, 这里的 $A$ 是 vector 了. 方向是垂直于平面. 为什么这里是垂直与平面?

因为最终求的是 $\phi$, 其垂直于平面, 这里就规定 A 是垂直于平面的, 这时又可以得到 $\theta$, 就有 $Ecos\theta$ 也是垂直于平面.

上面的公式考虑的是电场分布均匀的情况. 当不均匀, 我们就用到积分的知识:
$$
\phi_E \approx \sum_{i=1}^{n}E_i \cdot \Delta A_i
$$

也就是:
$$
\phi_E = \int E \cdot dA
$$

很多情况下, 我们计算的都是 closed surface 的 flux, 如: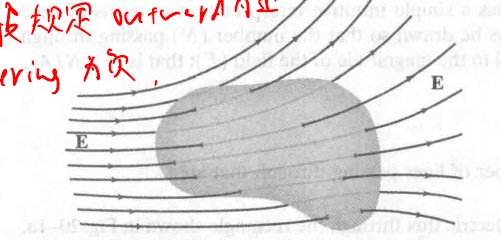

因此又可以写成闭合曲线积分的形式:
$$
\phi_E = \oint E \cdot dA
$$
E 和 $dA$ 之间的角度 $\theta$ 的值小于 $\frac{\pi}{2}$.

一般规定电场线 outward 为正, entering 为负.

只要封闭的曲线内部没有电荷, 那么总的 flux 就为 0 (进来了又出去).

内部有电荷, flux 就不会为零, 如: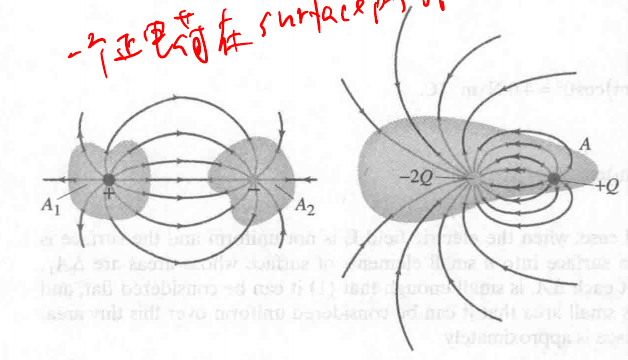

为什么叫 flux?

“flux” 这个词来源于拉丁语 “flow”. 也就是看作 fluid flow.

20.2 高斯定理 Gauss’s Law

公式内容:
$$
\oint E \cdot dA = \frac{Q_{encl}}{\epsilon_0}
$$
这里的 $Q_{encl}$ 表示的是 enclosed 的电荷量.

因为高斯定理适用于任一 surface (只要能把内部的电荷包裹起来就可以了, 毕竟计算的是 $\phi$ 是电场线的数量, 数量自然和 surface 没有关系), 就选取一个最容易计算的高斯面 (一般是球). 如: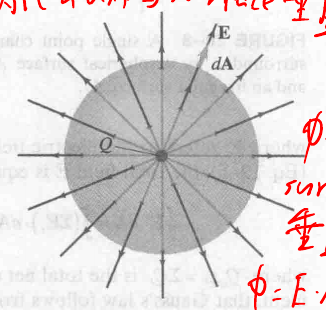

然后就有这样的推导:
$$
\oint E \cdot dA = \oint E dA = E \oint dA = E(4\pi r^2)
$$
为什么能直接将 $E \cdot dA$ 写成 $EdA$ ?

从球心到球面的连线即半径是垂直于 surface 的, 见上图, 电场方向和 surface 垂直方向相同.

我们知道:
$$
E = \frac{1}{4\pi \epsilon_0} \frac{Q}{r^2}
$$

就可以得到:
$$
E(4\pi r^2) = \frac{Q}{\epsilon_0}
$$

也就推出了高斯定理.

最后:
$$
\oint E \cdot dA = \oint \frac{1}{4\pi \epsilon_0} \frac{Q}{r^2} dA = \frac{Q}{4\pi \epsilon_0 r^2}(4 \pi r^2) = \frac{Q}{\epsilon_0}
$$

为什么能用理想的球推出来的高斯公式计算不规则图形 ?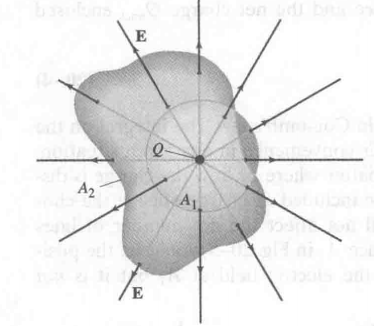

看图可知, 既然通过的电场线的条数相同, 用球计算出来的也就和不规则图形的相同.

Coulomb’s Law 不能描述由变化的磁场产生的电场. 但是 Gauss’s Law 适用于任何场景.

20.3 高斯定理的应用 Application of Gauss’s Law

为什么说高斯定理是描述 electric charge 和 electric field 的关系 ?

看公式就知道,
$$
\oint E \cdot dA = \frac{Q_{encl}}{\epsilon_0}
$$

左侧是 electric field, 右侧是 electric charge.

一般考虑 surface 为对称的, 这样 E 才会是 constant 或者在部分表面是均匀的.

重点在于计算出 $Q_{encl}$ 的值.

典型题

Spherical conductor

这种题, 是导体, 不管是空心还是实心, 都是一样的结果, 外部有电场, 内部电场为零:

求外电场, 主要就是选取高斯面, $r > r_0$, $r_0$ 是导体的半径.

选取的高斯面要包裹住原来的导体, 其内部的 $Q_{encl}$ 就是导体所带的电荷量.

Solid sphere of charge

这种是非导体, 但是电荷分布均匀, 计算外部的电场同样是直接选取 $r > r_0$ 的高斯面.

计算内部的电场时, 需要使用 charge density $\rho_E$, 且选取的高斯面 $r < r_0$:

Long uniform line of charge

题目如下:

书中的计算公式:
$$
\oint E \cdot dA = E(2\pi rl) = \frac{Q_{encl}}{\epsilon_0} = \frac{\lambda l}{\epsilon_0}
$$
为何公式仍然适用 ? 并没有用球形的高斯面 ?

暂时不清楚, (可能是和 Coulomb’s law 中的 k 的推导有关, 那么 k 和 $\epsilon_0$ 的关系是如何推导的) 似乎都能用这个式子计算. 选取的高斯面, 电场线最好垂直于 surface.

Infinite plane of charge

题目如下:

这里选取的高斯面是上下两个平面.

Electric field near any conducting surface

题目如下:

同样是直接应用高斯定理, 已知 surface charge density 为 $\sigma$:
$$
\oint E \cdot dA = EA = \frac{Q_{encl}}{\epsilon_0} = \frac{\sigma A}{\epsilon_0}
$$

最终得到:
$$
E = \frac{\sigma}{\epsilon_0}
$$

Chapter 21 电势能 Electric Potential

21.1 Electric Potential and Potential Difference

Potential energy can be defined only for a conservatice force.

Conservative force 做的功和路径无关, 与距离相关.

定义 potential energy 为 U.

定义的 $U_b - U_a$ 是从 a 移动到 b. 为什么 ?
可以理解为以前记忆的末减初就能得到中间的变化量.

为什么电场力做正功, potential energy 减小 ?
也就是说转换成了其他的能量. 比如电场力作正功时给粒子加速, 动能增大, 势能减少.

定义 electric potential (电势) 为 potential energy per unit charge:
$$
V_a = \frac{U_a}{q}
$$

只有电势差有物理含义

常用的公式:
$$
V_{ba} = V_b - V_a = \frac{U_b - U_a}{q} = - \frac{W_{ba}}{q}
$$

电势的单位是电压 volt:
$$
1V = 1 J/C
$$

常常把地面或连接到地面的导体视为电势为零.
$$
U_b - U_a = q(V_b - V_a) = qV_{ba}
$$
电荷经过 $V_{ba}$ 电势之后的势能变化量为 $qV_ba$.

一个类比:

在相同的高度, 重量越大的物体, 其重力势能越大 (mgh).
在相同电势的位置, 电荷量越大, 电势能也越大 ($qV_{ba}$.

注意, 在例题中有, 电子到某一点处的电势差为 $+5000V$, 一个质子到这一点处的电势差为 $-5000V$. 这可以用 $V = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r}$ 中看出.

21.2 Relation Between Electric Potential and Electric Field

$$
\because U_b - U_a = - w_{ba} = - \int_a^b F \cdot dl
$$

$$
V_{ba} = V_b - V_a = \frac{U_b - U_a}{q} = - \int_a^b \frac{F}{q} \cdot dl = - \int_a^b E \cdot dl = -E \int_a^b dl = -Ed
$$

记忆 $V = -\int E dl$ 技巧, $E dl$ 计算的是做的功, 而做的功和产生的势能是相反数. 因此有负号.

类型题

Charge conducting sphere

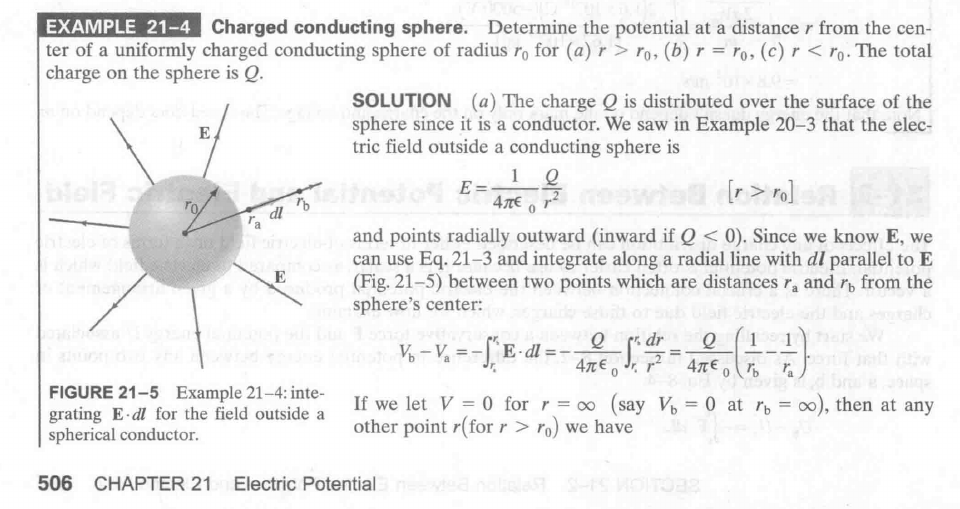
求外部电场 E 同样用到高斯定理, 内部电场为 0.

Breakdown voltage

在 high voltages 下, 空气会被电离形成电场. 被加速的电子会碰撞 $O_2$ 和 $N_2$, 使得更多的电子被撞出, 这时空气变成了导体, 有电流流动.

利用上一道题得到的结论:
$$
V = \frac{1}{4\pi \epsilon_0} \frac{Q}{r_0}, E = \frac{1}{4\pi \epsilon_0} \frac{Q}{r_0^2}
$$

可以得到:
$$
V = r_0 E
$$

21.3 Electric Potential Due to Point Charges

主要就是这个公式:

$$
V = \frac{1}{4\pi \epsilon_0} \frac{Q}{r}
$$

推导过程就是:
$$
V_b - V_a = - \int_{r_a}^{r_b} E \cdot dl = - \frac{Q}{4\pi \epsilon_0} \int_{r_a}^{r_b} \frac{1}{r^2} dr = \frac{1}{4\pi \epsilon_0}( \frac{Q}{r_b} - \frac{Q}{r_a})
$$
用来计算这种, 由一个带电物体产生的电场, 距离 r 处的电势: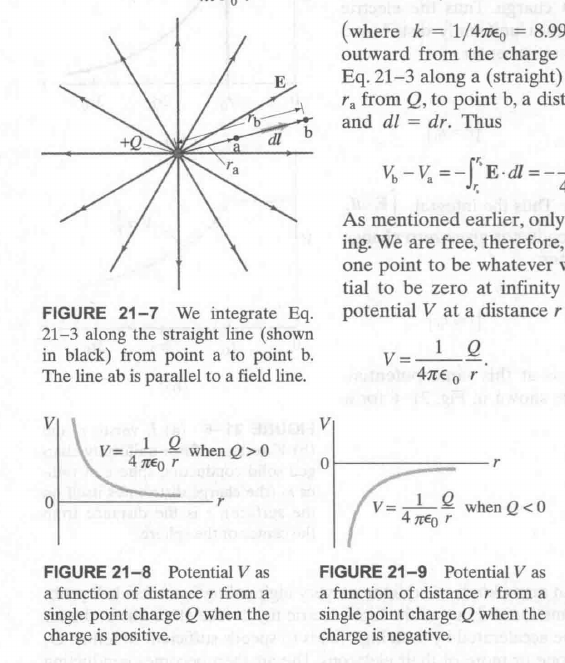

我们可以把产生电场的正电荷所在位置电势视为无限大 ($\infty$), 把无穷远处的电势视为 0.

电荷分布均匀的球体外部电场强度都相同.

习题 21-6

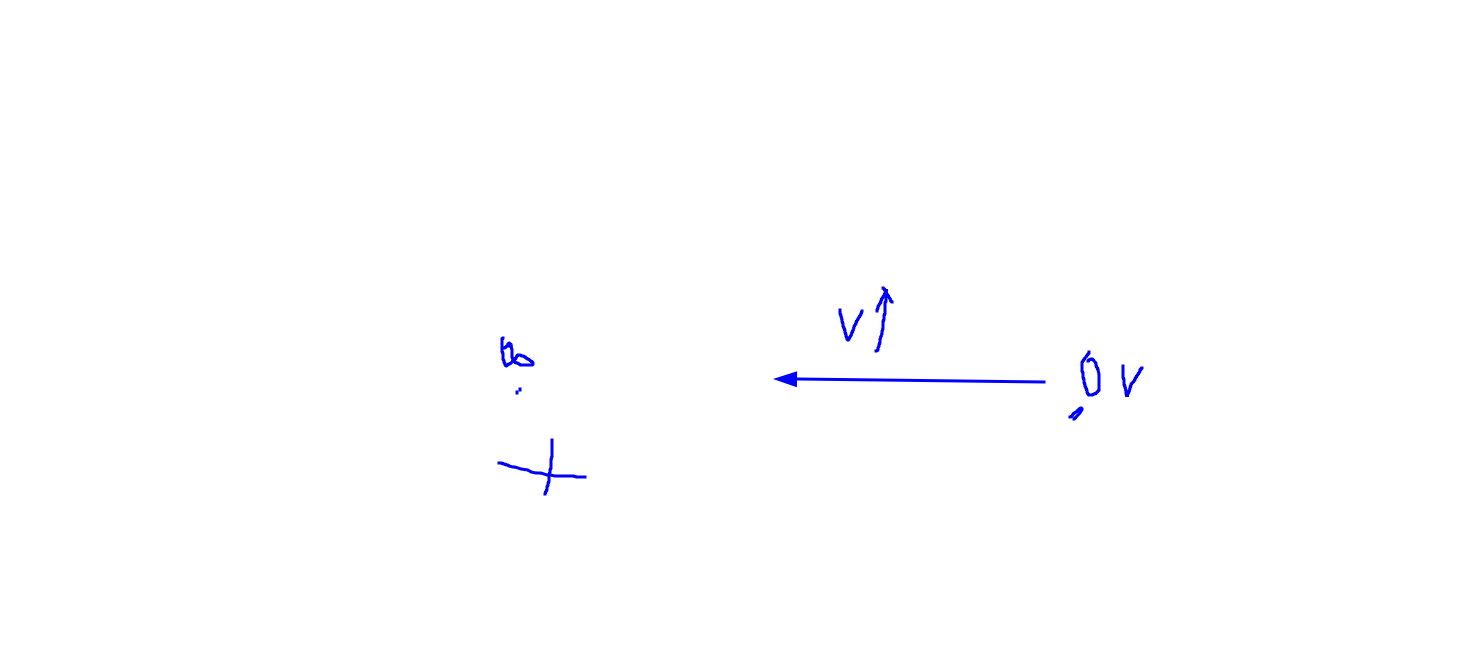
记住, 电势是 $J / C$ 就行.

习题 21-7

一个点处的电势来自于两个电荷. 已知电荷量求电势的题.

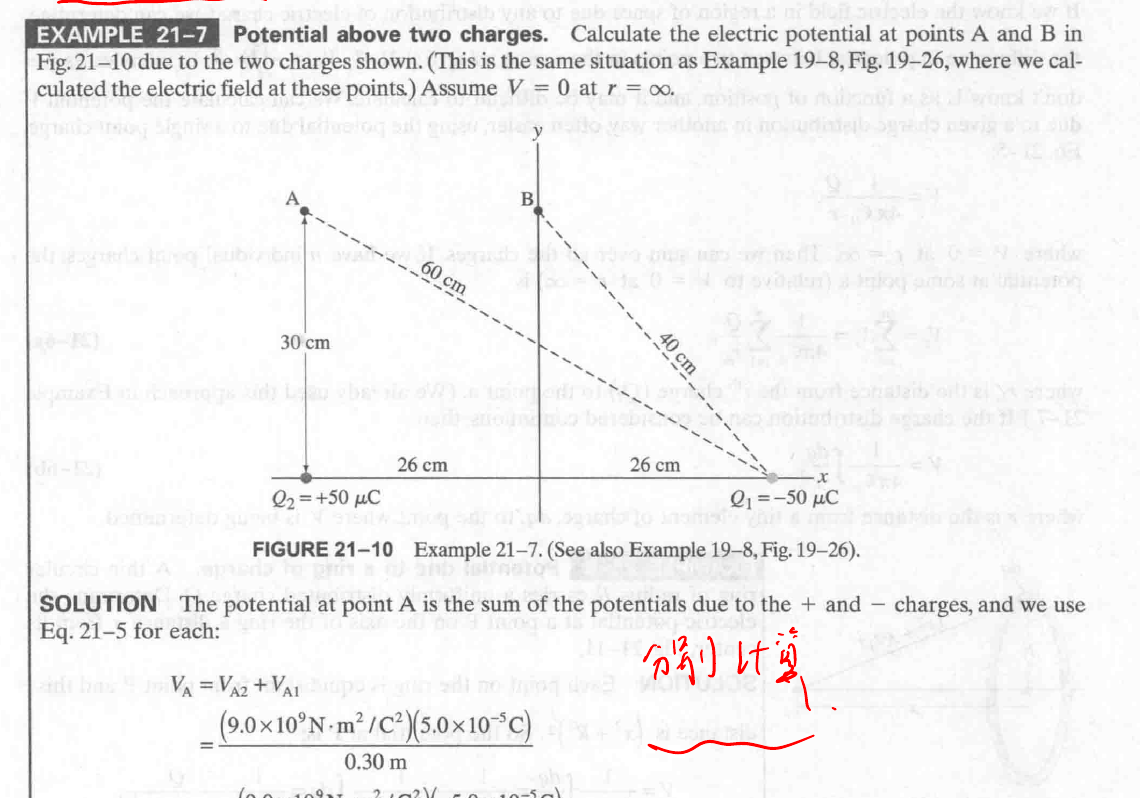
主要就是利用:
$$
V = \frac{1}{4\pi \epsilon_0} \frac{Q}{r}
$$
这个体现电势和电荷关系的公式.

分别计算两个电荷产生的电势并相加.

21-4 均匀分布的电荷产生的电势 Potential Due to Any Charge Distribution

也就是求存在多个 charge 的电场中的 potential.

根据已学的公式, 已知 Q 或 E 都能用于计算 V.
$$
V = \frac{1}{4\pi \epsilon_0} \frac{Q}{r}
$$
多个电场时公式变为:
$$
V_a = \sum_{i=1}^n V_i = \frac{1}{4\pi \epsilon_0} \sum_{i=1}^n \frac{Q_i}{r_i}
$$
这里就体现了将每个电荷作用的电势累加.

如果电荷是均匀分布的, 那就可以写为:
$$
V = \frac{1}{4\pi \epsilon_0} \int\frac{dq}{r}
$$

习题 21-8

charge 均匀分布在圆环上, 直接用公式积分就行:

习题 21-9

charge 均匀分布在圆盘上, 思路就是先求环的积分, 再求整个盘. 求环的积分, 求的是其上的电荷量.

利用二重积分计算的思路, 主要要求出单个点处的电势. 可以利用:
$$
\frac{dq}{dA} = \frac{Q}{A}
$$
这样的等式.

21.5 等势面 Equipotential Surfaces

电势能够通过画等势面来表示, 等势面就是这个面上所有的点, 其电势都相同.

面上两点之间的电势差为零, 在同一等势面上移动不做功.

等势面一定是和电场垂直.

理解为什么是垂直的?<\mark>

从前面可以知道, 等势面上所有的点的电势是相同的, 在其上的移动不做功, 如果电场不是垂直的, 如:

那么就会有在其移动方向上的分量, 就会做功, 不满足.

从 $\Delta V = - \int E \cdot dl$ 这个公式也能看出, 当 $\Delta V$ 为 0 时, 也就是两个向量相互垂直.

电场线的方向是从高电势指向低电势.

这里又提到了, 在静电场中, 导体内部的电场为零, 因为导体内的电荷是自由流动的, 若是收到了电场力的作用, 其会移动, 直到平衡.

导体的表面就是一个等势面. 电场线和导体表面始终垂直. (毕竟内部为 0, 向量垂直)

21.6 Electric Dipoles

还是和之前某一节中讲的相同的概念:

两个电荷, 具有相同的电荷量, 电性相反, 间隔 a distance $l$, 被称作 electric dipole.

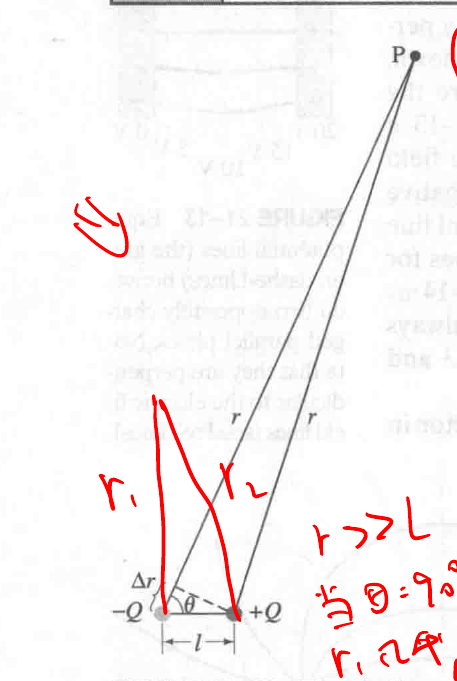
其通过用电荷量来计算电势的公式为:
$$
V = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r} + \frac{1}{4 \pi \epsilon_0} \frac{-Q}{r + \Delta r} = \frac{Q}{4 \pi \epsilon_0} \frac{\Delta r}{r( r+\Delta r )}
$$
这里, 当 $r$ 远大于 $l$ 时, 我们又知道 $\Delta r \approx l cos\theta$, 因此 $r >> \Delta r$, 就可以将其在分母部分忽略, 于是公式变成:
$$
V = \frac{1}{4 \pi \epsilon_0} \frac{Ql cos\theta}{r^2} = \frac{1}{4 \pi \epsilon_0} \frac{p cos\theta}{r^2}
$$
这里 $p = Ql$, p 就是 dipole moment.

从图中可以看出这里为什么是 $\Delta r \approx l cos\theta$, 当 $r >> l$ 时, $\theta \approx 90^\circ$, $r_1$ 和 $r_2$ 几乎平行.

$\theta$ 是负电荷那边的角度, 其决定了 $V$ 的正负值, 当其为 $0^\circ \sim 90^\circ$ 时, $V$ 为正, 其为 $90^\circ \sim 180^\circ$ 时, 为负.

dipole 的 potential 随 $r$ 的变化而变化得比单个 charge 更快:

dipole -> $\frac{1}{r^2}$

sigle charge -> $\frac{1}{r}$

习题 21-10

第一个问是已知 dipole moment 和 distance 求 dipole 的电荷量.
利用 $Q = \frac{p}{l}$ 可以计算.

第二问是已知距离求 potential, 先画图判断正负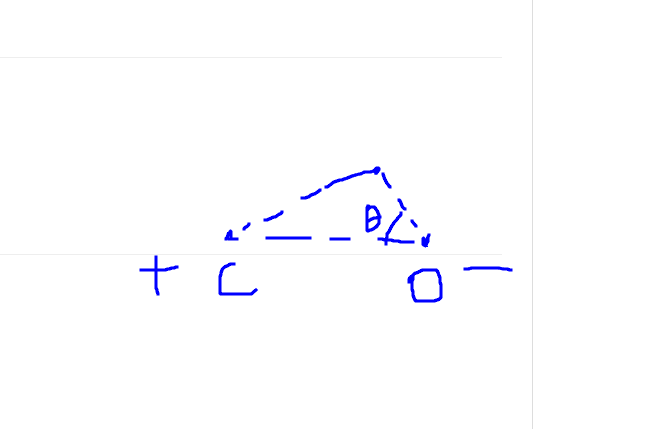

记住, $\theta$ 在靠近负电荷的那一边.

然后利用:
$$
V = \frac{1}{4 \pi \epsilon_0} \frac{p \cos \theta}{r^2}
$$
来通过 distance 和 dipole moment 算 potential.

21.7 E Determined from V

微分形式:
$dV = -E \cdot dl = -E_1 dl$
这里的 $E_1$ 是 $E$ 在 $dl$ 方向的分量.

可以写成:
$E_1 = - \frac{dV}{dl}$

这里的 $\frac{dV}{dl}$ 也被称为 V 在某个特定方向的梯度. 如果方向没有指明, 这里就指 V 变化最快的方向.

如果 E 是 $x,y,z$ 的方程, 那么:

$E_x = - \frac{\partial V}{\partial x}$, $E_y = - \frac{\partial V}{\partial y}$, $E_z = - \frac{\partial V}{\partial z}$

习题 21-11

利用这两个图: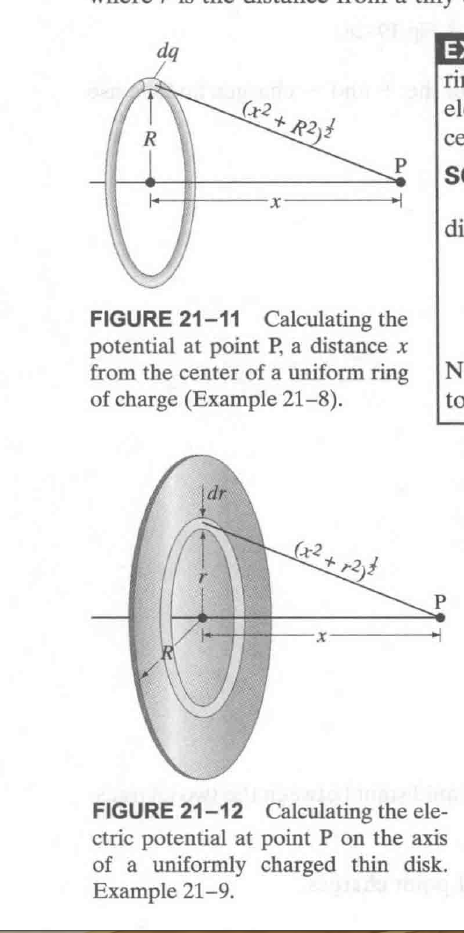

只不过使用 $x,y,z$ 的方程计算. 一般先算出 V, 再计算 E. (V 是标量, E 是矢量).

这里提到了 gradient operator: $\Delta = i \frac{\partial}{\partial x} + j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z}$

21.8 电势能, 电子伏特 Electrostatic Potential Energy; the Electron Volt

这一节将 $eV$ 这个单位. 为什么要引入这个单位 ?

用来表示一个电子所做的功.

若系统中只有一个电荷, 那么也就不存在 potential energy, 但如果系统中有两个电荷:

$V = \frac{1}{4 \pi \epsilon_0} \frac{Q_1}{r_{12}}$

$r_{12}$ 是两个电荷的距离:

$U = Q_2 V = \frac{1}{4 \pi \epsilon_0} \frac{Q_1 Q_2}{r_{12}}$

如果有三个, 那么总的 potential energy 就是:
$$
U = \frac{1}{4 \pi \epsilon_0} ( \frac{Q_1 Q_2}{r_{12}} + \frac{Q_1 Q_3}{r_{13}} +\frac{Q_2 Q_3}{r_{23}} )
$$
两两组合.

$1 eV = 1.6 \times 10^{-19} J$