运算放大器
参考 B 站1
运算放大器是一个集成期间,它是由诸多晶体器件 (如晶体管) 所构成.
从外部特性来看,运算放大器是一个具有:
- 三个信号端子
- 两个电源端子
的器件.
它有:
- 两个具有高输入电阻的电压信号输入端.
- 一个具有低输出电阻的电压信号输出端
- 正负两个电源端
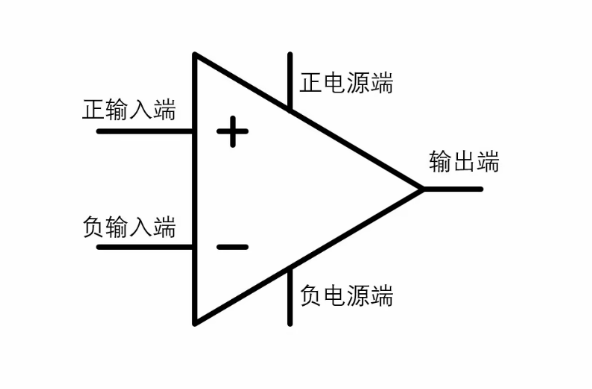
需要注意,并不是所有运算放大器的输入端都具有高输入电阻.
参考 B 站2
放大器可以将信号放大, 为什么又叫运算放大器? 是由于其常被用来模拟加, 减, 微分,积分运算。
放大器中的电源和输入是什么区别?
自己简单理解为,放大器是一个简化的电路 (不是说结构简单,而是封装的含义,内部的电源细节没有展现出来), 其内部的电路需要供电.
如 741 放大器的内部电路:
参考 B 站3
运算放大器的输入端永远没有电流 (输入和输出电流都没有), 输出端可以有电流的输入和输出: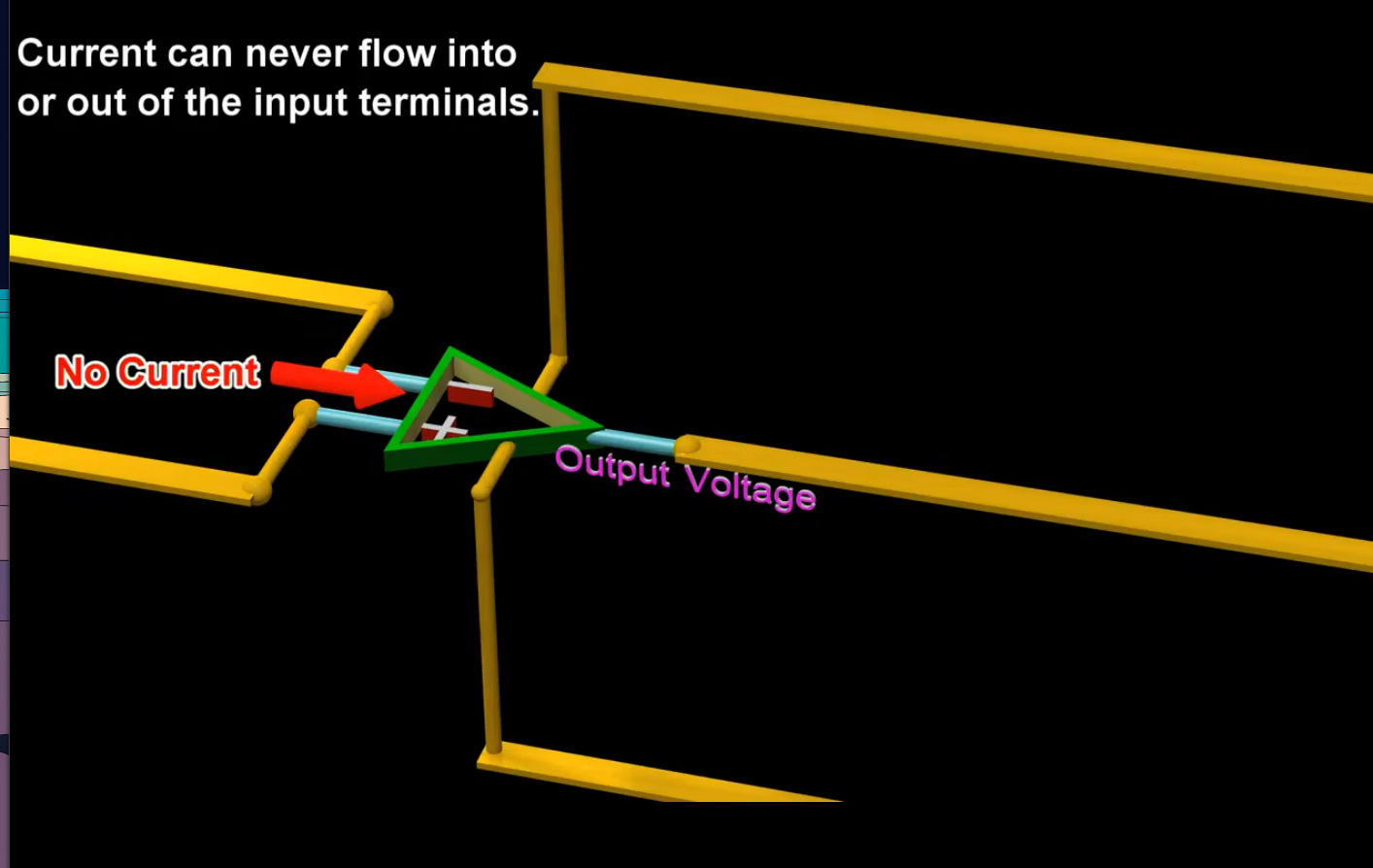
从输出端流入或流出的电流由运算放大器的供电端提供.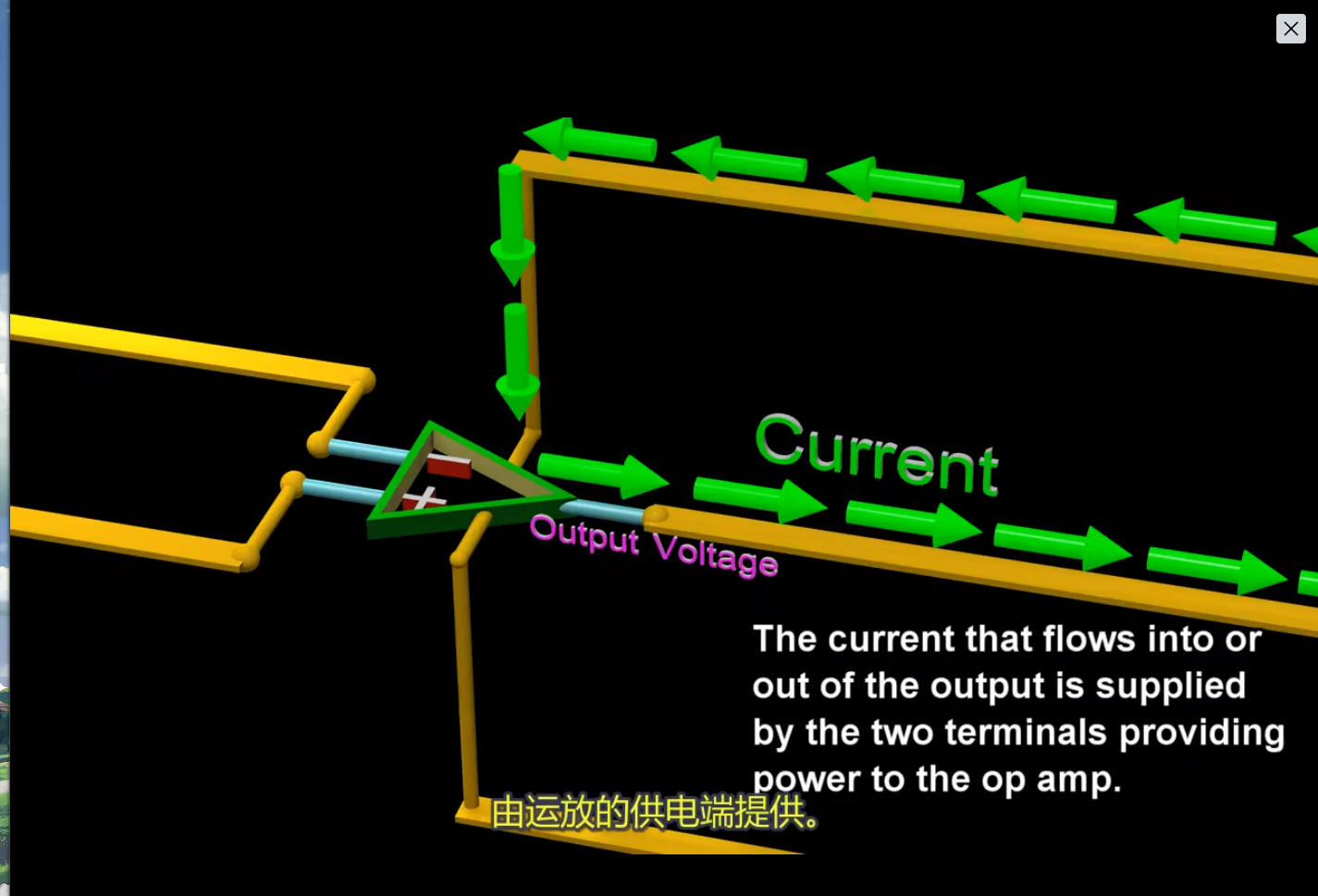
给运算放大器供电的两个端子通常没有显示出来.
运算放大器产生的 output voltage 的大小在两个电压端子提供的电压之间.
运算放大器将带 “+” 号一端的输入端电压与带 “-“ 号一端的输入电压相减: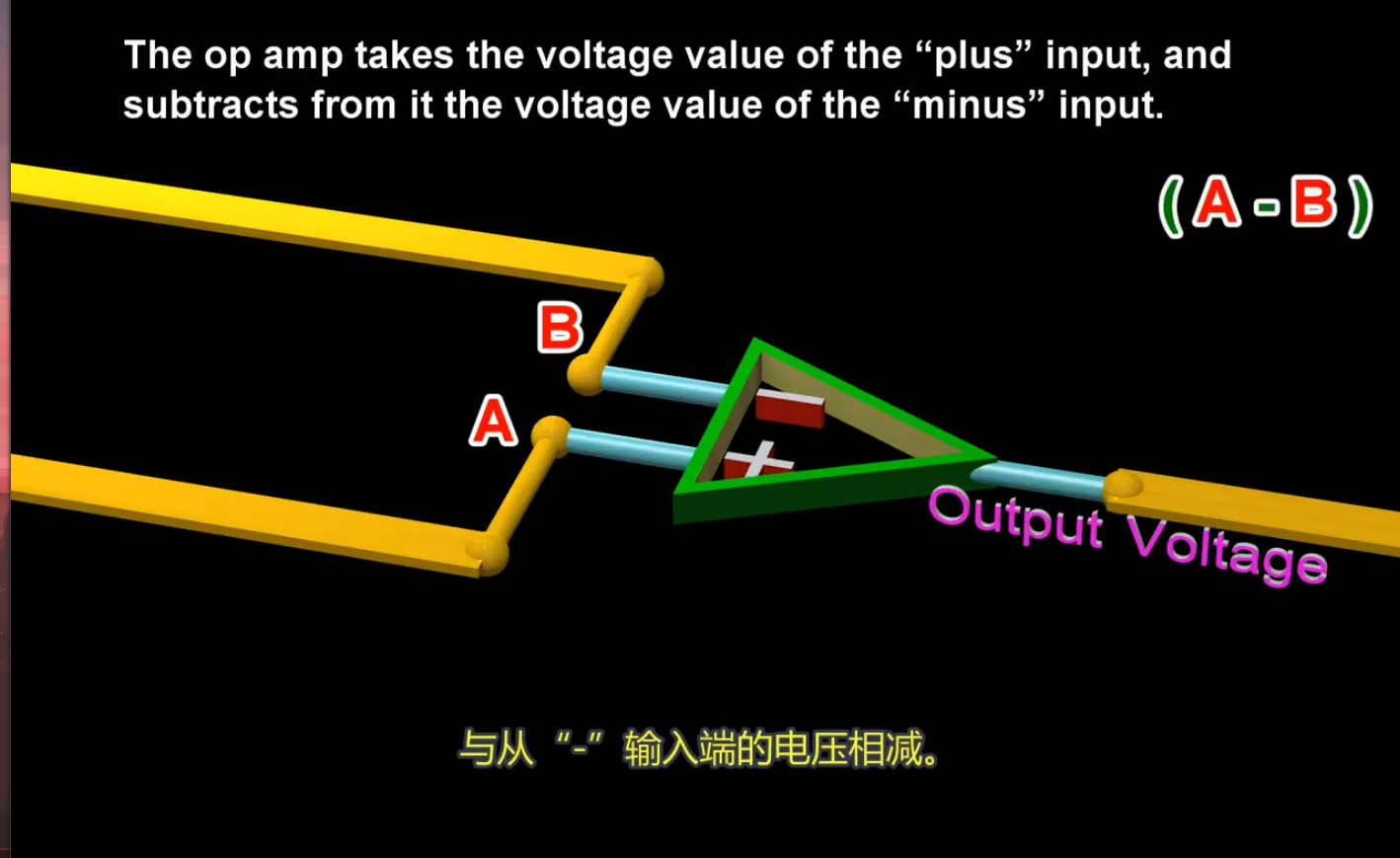
运算放大器会用这个差值来乘以一个非常大的数字,得到了一个结果:
$$
\Delta V \times k (a\ big\ num)= result
$$
运算放大器输出的电压就会等于这个结果的值.
这意味着:
- 如果 Vin+ < Vin-, 结果为负数, 输出电压就为一个极大的负电压
- 如果 Vin+ > Vin-, 结果为正数, 输出电压就为一个极大的正电压
这里需要一个称为 negative feedback (负反馈) 的概念. 如: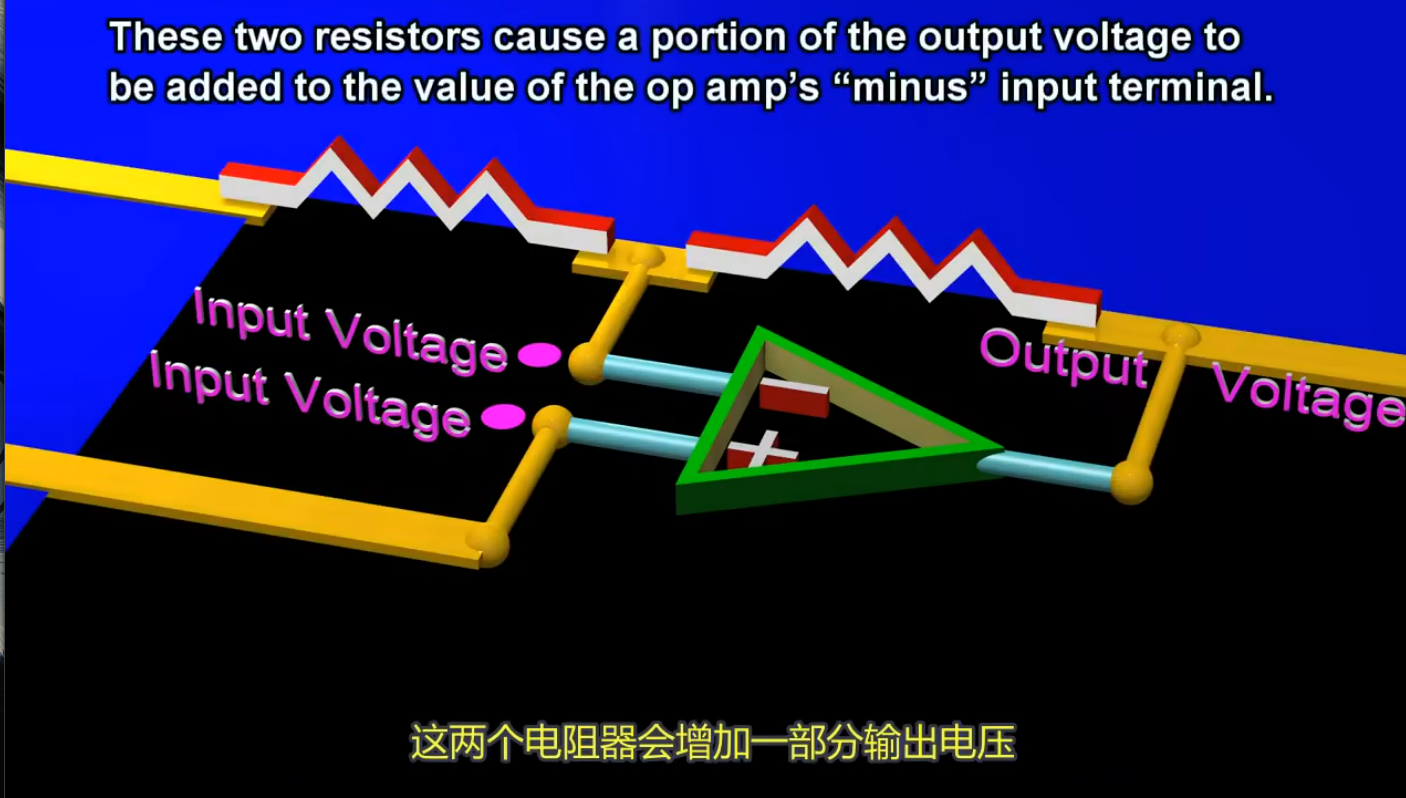
这两个电阻,使得产生的输出电压的一部分又加回到 “-“ 一端的输入端.
这时考虑:
若 “+” 输入端电压变得低于 “-“ 输入端电压,那么输出端的电压会下降,从输出端加回到 “-“ 输入端的电压就会下降,直到 “-“ 输入端几乎与 “+” 输入端恰好相等, 输出电压将停止下降.
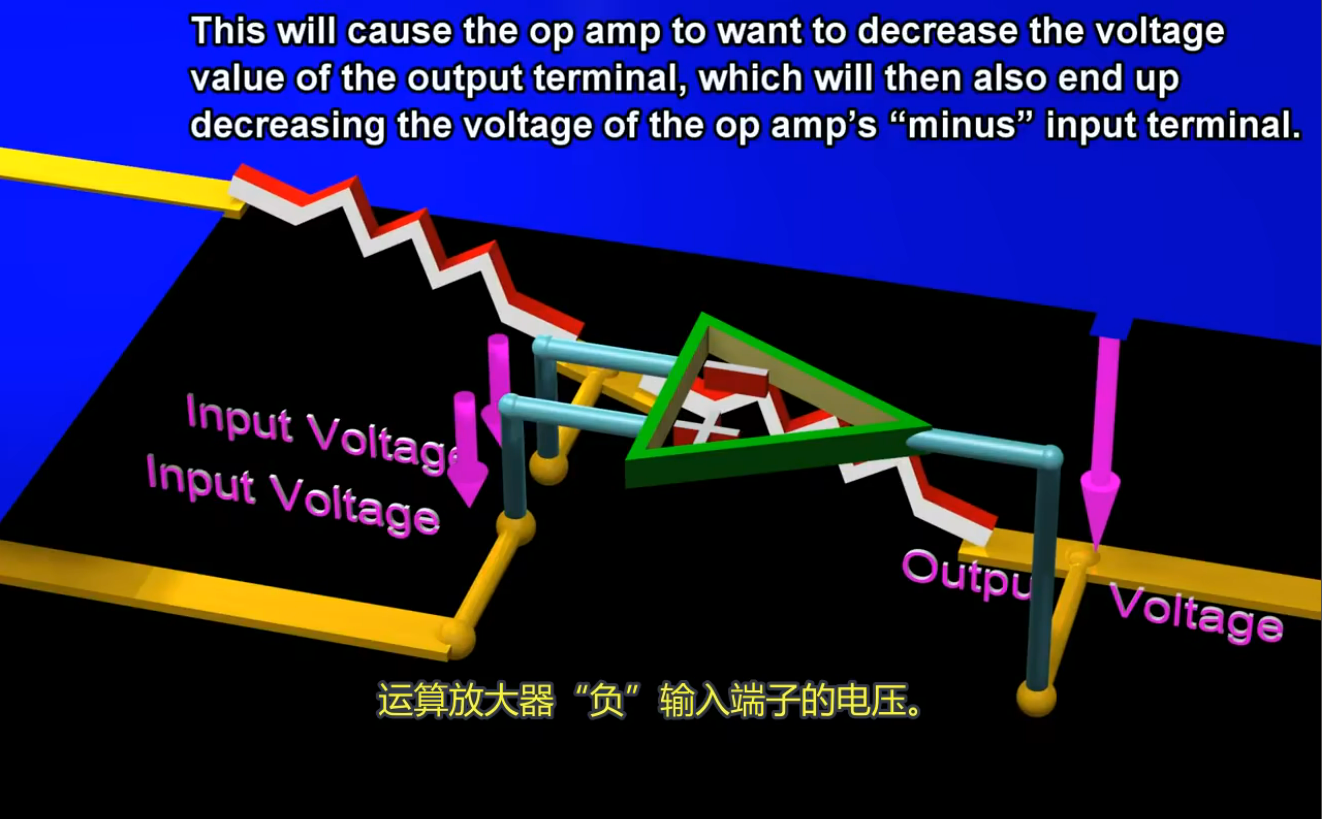
又假设 “+” 输入端的电压高于 “-“ 输入端, 这会使放大器将输出电压增大, 这同时会使 “-“ 输入端的电压增大,直到其等于 “+” 输入端的电压大小.
总结, 负反馈的存在总是迫使运算放大器的两个输入端子始终处于几乎相同的电压值. 一旦运算放大器的两个输入端子的电压几乎达到相同的值,他们之间的差值就是一个非常小的数字,因此输出电压就会是这个非常小的数字乘以一个非常大的数字.
看这一个情况: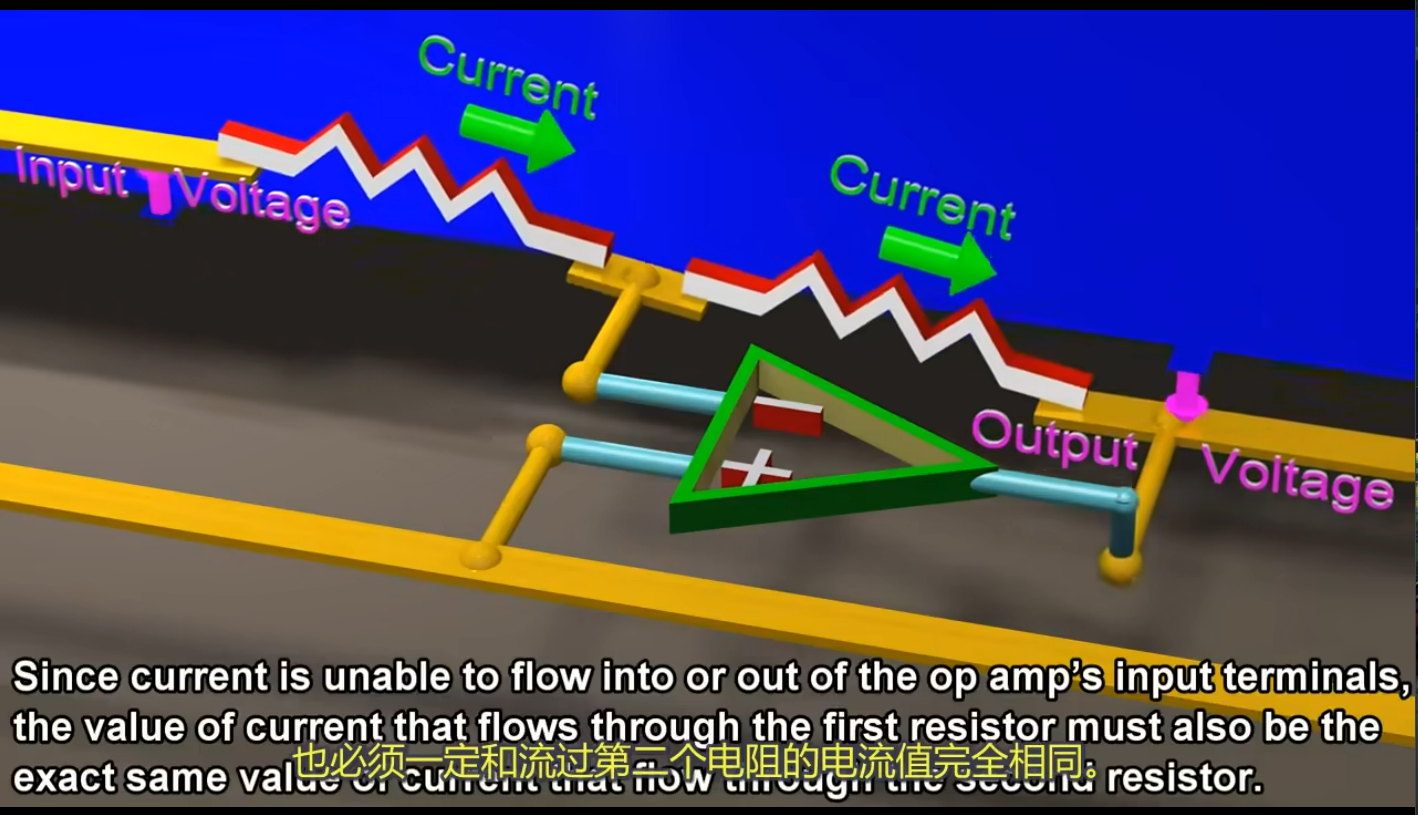
由于电流不会流过放大器的输入端,流过第一个电阻的电流值一定和流过第二个电阻的相同. 每个电阻的压降等于 $RI$.
从这个图中: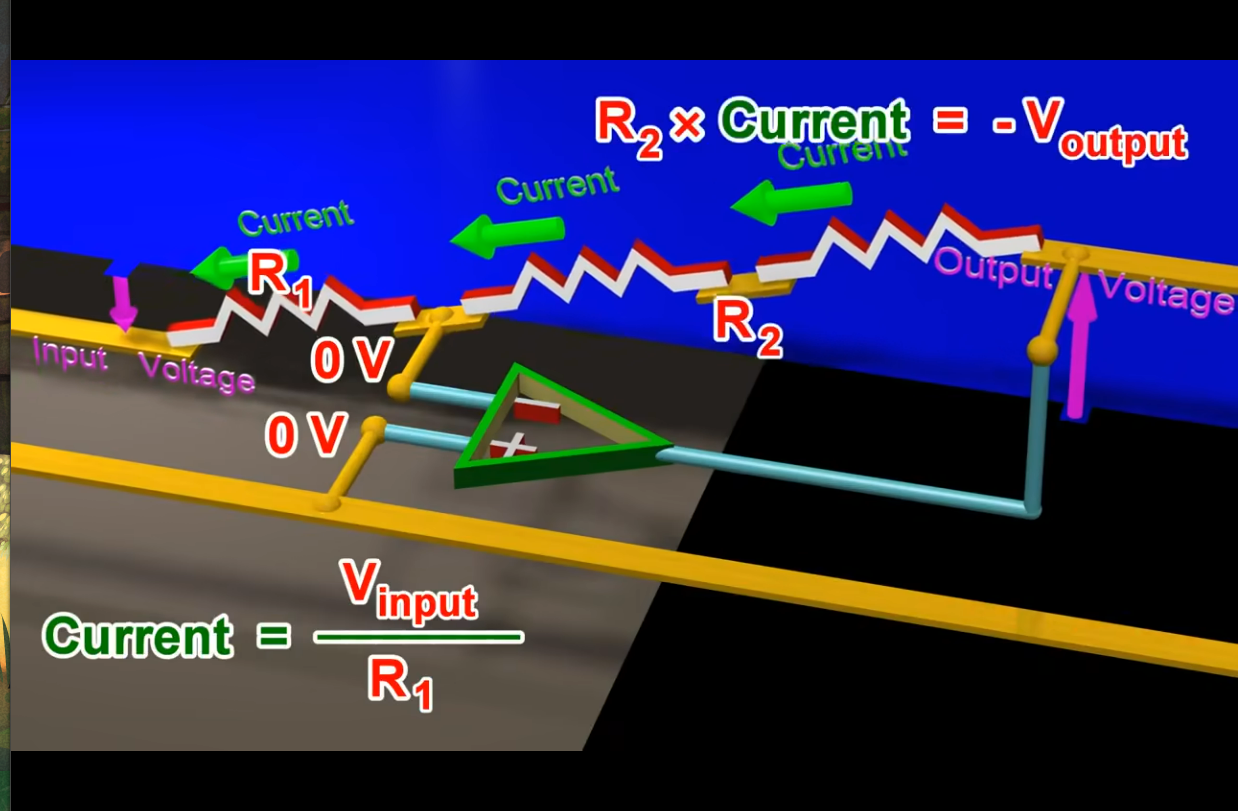
若 R2 是一个大电阻,那么 Vout 输出电压基本都会被这个大电阻分压. 因此 R2 的电压基本等于输出电压.
$$
\because I_{in} = \frac{V_{in}}{R1} \newline
-V_{out} = I_{in} R2 \newline
\therefore V_{output} = - \frac{V_{in}}{R1} \times R2 = - \frac{R2}{R1} V_{in}
$$
注意这里的输出电压为负的,因为输入电压 Input Voltage 是连接在 “-“ 输入端.
如果要让输出电压为正,则需要改变输入电压的位置到 “+” 输入端.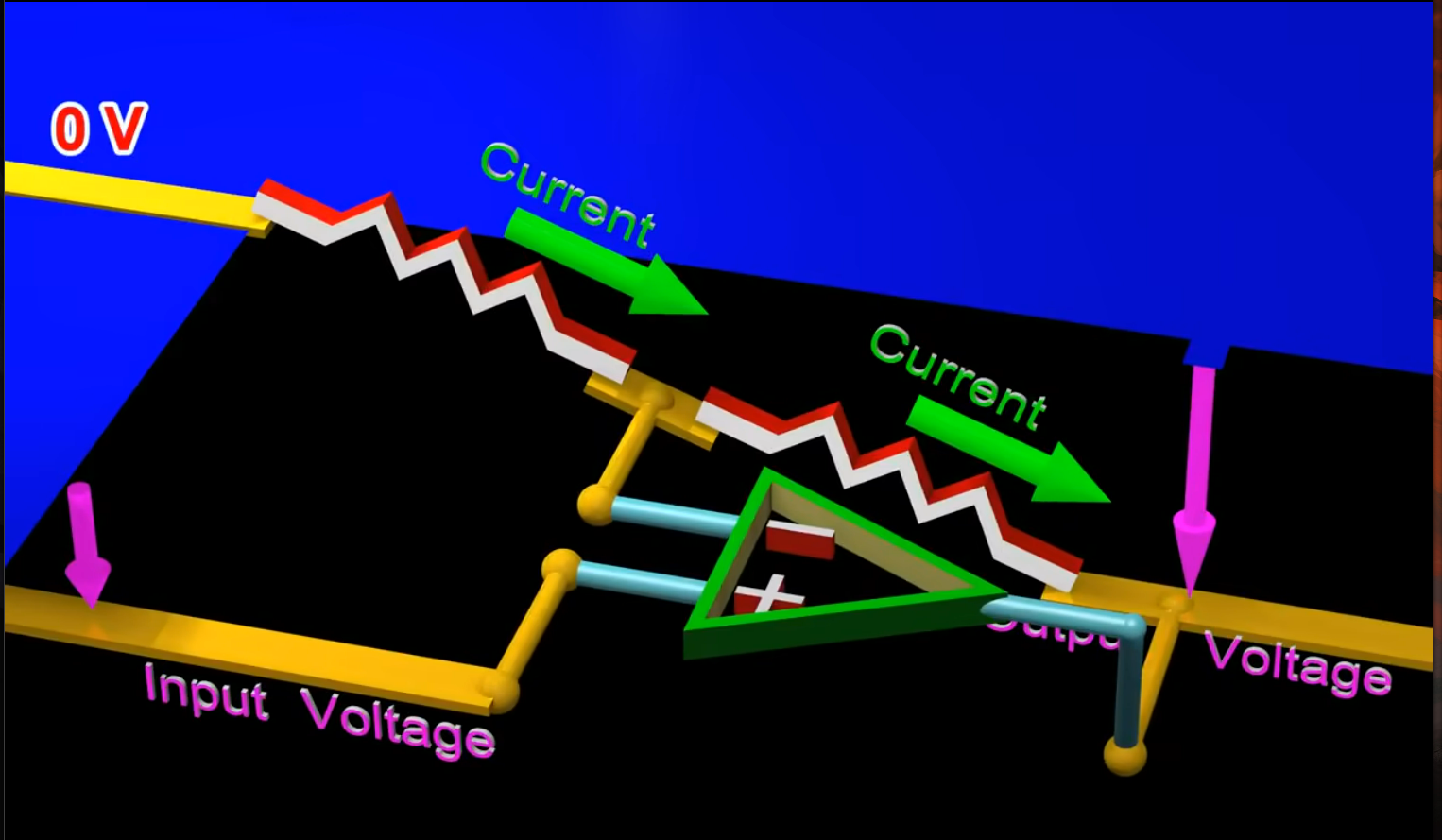
此时:
$$
I = \frac{V_{input}}{R_1} \newline
V_{output} = I \times (R_1 + R_2) \newline
V_{output} = (1 + \frac{R_2}{R_1}) \times V_{input}
$$
输出电压是所有输入电压的总和:
积分运算
一个电阻和电容如下: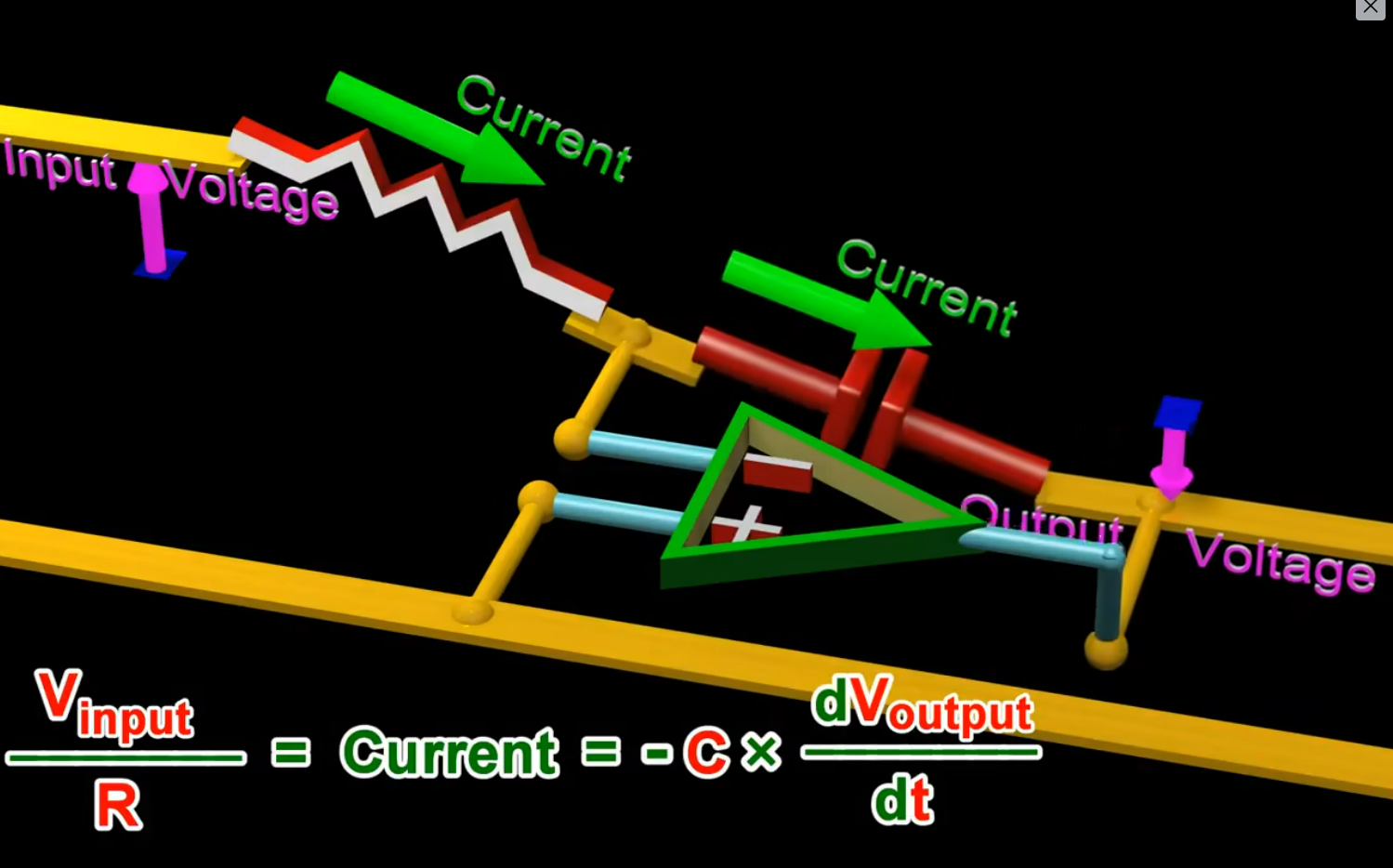
计算如下:
$$
\frac{V_{input}}{R} = I = -C \times \frac{dV_{output}}{dt} \newline~
\newline
V_{output} = - \frac{1}{RC} \int V_{input}dt
$$
微分运算
交换电阻和电容的位置:
计算如下:
$$
C \times \frac{dV_{input}}{dt} = I = - \frac{V_output}{R} \newline~
V_{output} = - RC \times \frac{dV_{input}}{dt}
$$
充当缓冲器使用
这种情况下,输出电压恰好等于输入电压:
反向放大器
Inverting amplifier, 因为输出电压和输入电压符号相反,所以为 Inverting, 反向放大器.