相对论和量子力学
量子力学和相对论的开端
开尔文爵士提出两朵乌云:
- 黑体辐射 –> 量子力学
- 迈克尔孙实验 –> 相对论
黑体: 只吸收和辐射电磁波,但是不反射.
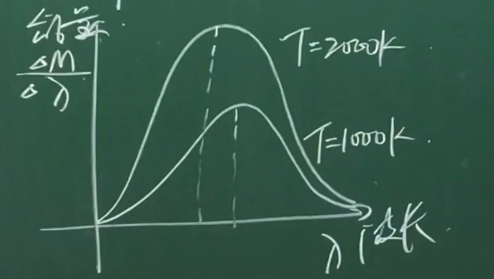
瑞利和金斯利用经典电动力学推导出的 “瑞利-金斯公式”, 和黑体辐射变化图像不符,这里同时出现了 – “紫外灾难”
普朗克,引入假设,振动的带电粒子,能量不是连续的,能量是一份一份的,其能量表示为:
$$
\displaylines{\epsilon = hv}
$$
$\epsilon$ 是振动带电粒子的能量, $h$ 是普朗克常数, $v$ 是振动的频率.
而这一份能量就被称为 能量子, 即量子. 同时完美解释了黑体辐射问题.
爱因斯坦解释光电效应, 光照射金属板,金属板释放电子,其很多结论用传统理论无法解释,如能不能发射电子是跟频率有关,而传统理论认为光的能量由光强决定,不是频率决定.
爱因斯坦引用普朗克的理念,认为光也是一份一份的,每一份称为光子,每一个光子的能量也是普朗克常量乘以光的频率, 通过这种方法,爱因斯坦解释了光电效应.
他说既然光本身具有波动性电磁波,同时它还具有粒子性. 于是爱因斯坦说光具有波粒二象性.
狭义相对论
相对论主要讲从两个参考系来观察物体:
- 物体本身作为一个参考系
- 地面参考系
爱因斯坦的两个基本假设 (狭义相对论的两个基本假设):
- 相对性原理, 物理规律在不同的惯性参考系下,具有相同的形式 (惯性参考系指静止或匀速直线运动的参考系, 形式相同指表达式相同)
- 光速不变原理, 在真空中,任何惯性参考系下,光速都是一样的,为 $3 \times 10^8 m/s$
形式相同解释:

火车参考系下的 $s$, $v$ 和地面参考系下都不同,但是却用同一个表达式计算.
光速不变,不同参考系下同时性被破坏
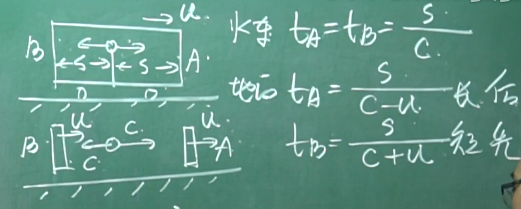
在火车参考系下,两束光同时到达,而在地面参考系下,没有同时到达.
长度收缩
运动物体在运动方向上长度收缩. 在静止参考系上观察物体,是本征长度 $L_0$, 在地面参考系上看物体的长度为非本征长度 $L$, 它会缩短, $u$ 是相对速度:
$$
\displaylines{L = \sqrt{ 1 - ( \frac{u}{c} )^2 }}
$$
可以看出,相对速度越大,长度 $L$ 就越小.
长度收缩引发的悖论 – 火车隧道悖论

有一个火车和一个隧道,这个火车和隧道都是完全一样长的,本征长度都是 $L_0$, 那么如果火车运动着开过了隧道,谁会变短?
(似乎以谁为参考系, 谁的长度就不变, 为本征长度)
从隧道看来,隧道还是 $L_0$ 长,火车变短了
从火车看来,火车还是 $L_0$ 长,隧道缩短了
解释为,在隧道看来同时发生的事,在火车看来不是同时发生的。
狭义相对论,时间膨胀

时间膨胀,意思是,运动的物体的时间会变慢. 如,运动的物体,它认为过了一分钟,地面上的人认为过了十分钟.
一列火车向右运动,火车上一处,向上发射一束光,遇到顶部后反弹.
在火车参考系下看,光的出发点和落地点是同一个点,其经过的时间为:
$$
\displaylines{t_0 = \frac{2s}{c}}
$$
$t_0$ 为本征时间. ( $s$ 为上下的距离, $c$ 为光速)
在地面参考系下看,光的出发点和落地点是不同点, 此时求得的时间为非本征时间, 计算为:
$$
\displaylines{t = \frac{2s}{\sqrt{c^2 - v^2}}}
$$
$c$ 是光速, $v$ 是水平速度分量 (为了和火车相对静止运动)
时间膨胀就是指:
$$
\displaylines{ \frac{t_0}{t} = \frac{\sqrt{c^2 - v^2}}{c} = \sqrt{1 - ( \frac{v}{c}^2 )} < 1}
$$
即本征时间小于非本征时间,即时间膨胀. (观察者位于地面参考系, 观察者观察到的时间大于运动者认为的时间)
时间膨胀公式
$$
\displaylines{ t = \frac{t_0}{\sqrt{ 1 - ( \frac{v}{c} )^2 }} }
$$
这里的 $t$ 就是观察者观察的时间.
双生子佯谬
当一个物体出现变速过程时,不能用狭义相对论求解,必须用广义相对论求解.