洛伦兹变换-Notes
先导知识: 波速取决于介质的速度,而不是波源的速度
如你跑步时说话,声音的传播速度并没有变 (你是波源,空气是介质).
而如果你迎风说话,声音的传播速度或增大 (介质的速度变大)
真空中的光靠什么介质传播
没有传统意义上的介质.
光速不便的背后是我们相信电磁学规律不回因为惯性参考系的变化而变化, 即麦克斯韦方程组在不同惯性系下保持同样的形式,方程内的常数也保持不变.
洛伦兹变换的推导
看完博文后仍有些不理解, 但大致如下:
从地面参考系观察
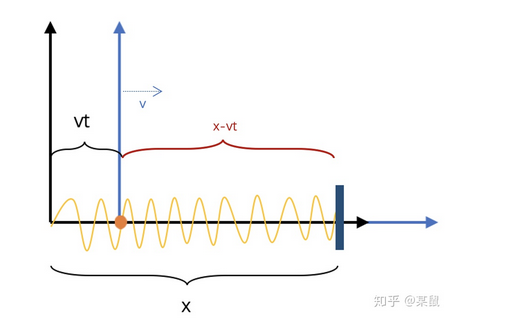
黑色坐标系是你站在地面上的位置,蓝色坐标系是火车,火车在经过你时向前进方向发出了一个闪光,橙色点是光源位置 (此时不再闪光). 光运动 $t$ 时间后到达石头.
光的初始位置是黑色坐标系原点,终止位置是石头:
$$
\displaylines{x = ct}
$$
$vt$ 是你和火车的距离, $x - vt$ 是火车和石头的距离.
从火车参考系观察
光运动 $t^\prime$ 后到达石头:
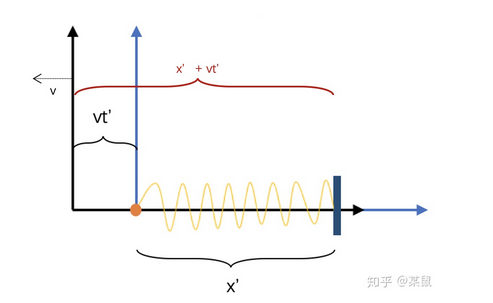
光的初始位置是蓝色坐标系原点, 即火车,终止位置是石头.
$$
\displaylines{x^\prime = c t^\prime}
$$
也就是说,不同参考系下,起始位置不同,导致运动的距离不同
比较火车到石头的距离的矛盾之处
如果两个失控的度量相同,那么火车到石头的距离是相同的, 即:
$$
\displaylines{x-vt = x^\prime \newline~ \newline ct - vt = ct^\prime \newline~ \newline t = t^\prime \newline~ \newline vt = 0}
$$
但 $v$ 和 $t$ 都不一定为零 (这一部分不是很懂)
为了解决矛盾,爱因斯坦认为两个时空的度量不同,在这两个参考系下观察火车到石头的距离差了一个线性的缩放系:
$$
\displaylines{x^\prime = \gamma \cdot (x - vt) \newline~ \newline x = \gamma \cdot (x^\prime + vt^\prime)}
$$
(公式不是很理解)
推导结论
$$
\displaylines{
\begin{cases}
x^\prime = \gamma \cdot (x - vt) \newline~ \newline
x = \gamma \cdot (x^\prime - vt^\prime)
\end{cases}
}
$$
推导见博文吧,没怎么理解到这里就直接写结论:
正变换
$$
\displaylines{
\begin{cases}
x^\prime = \frac{x - vt}{\sqrt{1 - \frac{v^2}{c^2}}} \newline~ \newline
y^\prime = y \newline~ \newline
z^\prime = z \newline~ \newline
t^\prime = \frac{ \frac{-v}{c^2} \cdot x + t }{\sqrt{1 - \frac{v^2}{c^2}}}
\end{cases} }
$$
逆变换
$$
\displaylines{
\begin{cases}
x = \frac{x^\prime - vt^\prime}{\sqrt{1 - \frac{v^2}{c^2}}} \newline~ \newline
y = y^\prime \newline~ \newline
z = z^\prime \newline~ \newline
t = \frac{ \frac{-v}{c^2} \cdot x^\prime + t^\prime }{\sqrt{1 - \frac{v^2}{c^2}}}
\end{cases} }
$$
应用
可以用洛伦兹变换推导出:
- 运动物体变短
- 时间膨胀
等.