大物II上半期-Notes2

Chapter 22 Capacitance, Dielectrics, Electric Energy Storage

22.1 Capacitors

重要公式

$$
\displaylines{C = \frac{Q}{V}}
$$
(C 指电容量, Q 指电荷量, V 指电势差)

A capacitor 有时也被称为 condenser, 可以存储 electric charge, 常常由两个导体, 放得接近但是不接触组成.

非常小的 capacitors 用来电脑 RAM 中存储 0 和 1 的二进制.

常常两个板子卷成圆柱体, 中间夹着纸或者其他 insulator:

capacitor 的 symbol 为:

不能将电源和电容器混淆. 电容器只是存储电荷的电子元件.

将电源和 capacitor 联通可以充电:
$$
Q = C V_{ab}
$$

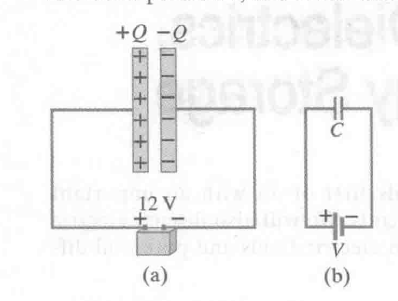
这里的 $C$ 就是 capacitance of the capacitor. 单位是 $C / V$, 即 $F$, a farad.

$C$ 的值取决与 capacitor 的大小, 形状, 两个导体的相对距离, 以及材料.

22.2 Dtermination of Capacitance

最终公式

$$
C = \frac{Q}{V_{ba}} = \epsilon_0 \frac{A}{d}
$$

推导电容量影响因素的公式

得出这个推导式, 主要是对 $C = \frac{Q}{V}$ 中的 $V$ 进行变换. 也就是会影响电势差的因素.

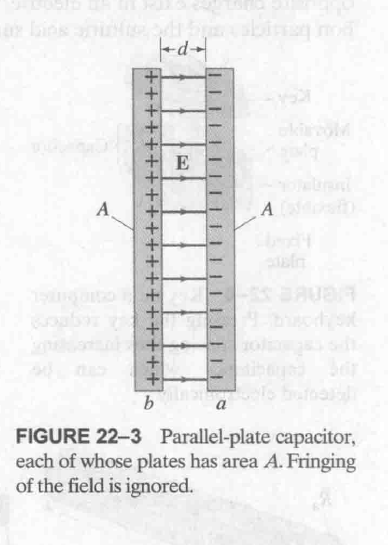
这里假设 capacitors 的形状简单, 之间的 insulator 为真空或空气, 两个 conductor 之间的距离 $d$ 很短, 每一个 plate 的面积为 A.

根据 $E = \frac{\sigma}{\epsilon_0}$ 和 $\sigma = \frac{Q}{A}$ 得到:
$$
E = \frac{Q}{\epsilon_0 A}
$$
又因为:
$$
V_{ba} = - \int_a^b E \cdot dl
$$
这里是点乘, 也就是向量, 需要知道 E 和 $dl$ 之间的角度, 从图上可以看出, a -> b 的方向和 E 的方向相反, 则 $\theta = 180^\circ$, 即 $\cos 180^\circ = -1$:

则有:
$$
V_{ba} = V_b - V_a = -\int_a^b E dl \cos 180^\circ = +\int_a^b E dl = \frac{Q}{\epsilon_0 A} \int_a^b dl = \frac{Q d}{\epsilon_0 A}
$$

最终:
$$
C = \frac{Q}{V_{ba}} = \epsilon_0 \frac{A}{d}
$$

习题 22-1

(a) 已知面积 A 和 distance d 求 capacitance. 利用 $C = \epsilon_0 \frac{A}{d}$ 计算.

(b) 已知 C 和 V 计算 Q.

(c) 已知 Q 计算 E.

习题 22-2

这道题是让我们推导出一个计算 C 的公式, 一个重点在于求 a long wire 外的电场:

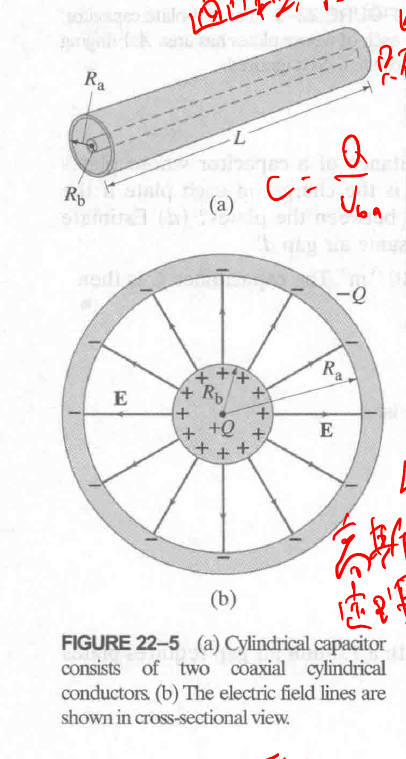
下面的那个是截面图.

a long wire 外的电场的推导式为:
$$
dq = \lambda dl
$$
形成的电场 $dE$ 为:
$$
dE = \frac{1}{4 \pi \epsilon_0} \frac{dq}{r^2}
$$

因为 $E_y = 0$ 我们可以知道:
$$
E = E_x = \int dE \cos \theta
$$
又 $y = x \tan \theta$, 具体看书, 约去一部分后就有了:
$$
E = \frac{1}{2 \pi \epsilon_0} \frac{\lambda}{x}
$$

习题 22-3

这道题是两个同心球, 图像同样是截面图:

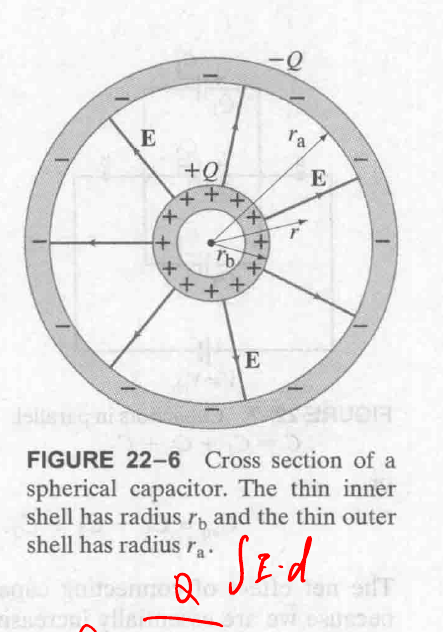
主要还是先求电场, 然后再利用 $V_{ab} = -\int E \cdot dl$ 来求电势.

这里求电场用的是高斯定理. 其算出, the electric field outside a uniformly charged conducting sphere is $E = \frac{Q}{4 \pi \epsilon_0 r^2}$.

只有一层 conductor 的也可以计算 capacitance, 只不过假设与另一层的距离为 $\infty$. 但其不能被视作是 capacitor.

22.3 Capacitors in Series and Parallel

最终公式

并联:

$$
C_{eq} = C_1 + C_2 + C_3
$$

串联:

$$
\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{c_2} + \frac{1}{C_3}
$$

主要是将并联和串联的 capacitors 转换成等效的一个 capacitor.

capacitors 并联 :

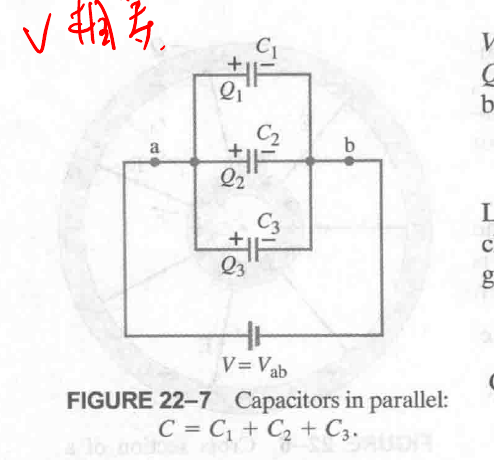
由于 capacitors 的正极板的电势相等:
$$
Q = Q_1 + Q_2 + Q_3 = C_1V + C_2V + C_3V
$$
又有:
$$
Q = C_{eq} V
$$
则:
$$
C_{eq} V = (C_1 + C_2 + C_3)V
$$
得到:
$$
C_{eq} = C_1 + C_2 + C_3
$$

capacitors 串联:

利用每一个 capacitor 的 Q 相同得出:
$$
\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{c_2} + \frac{1}{C_3}
$$
串联之后, C_{eq} 比任何一个串联的 capacitor 都要小.

习题 22-6

当两个 capacitor 充好电之后, 将这两个 capacitor 相连, 只不过是一个的正极板接另一个的负极板, 求 $q_1$ 和 $q_2$ 的值:

解题

切入点是 $V^\prime$ 相等, 已知 $C_1$ 和 $C_2$:
$$
\displaylines{q_1 = C_1 V^\prime \newline~ q_2 = C_2 V^\prime \newline~ q_1 + q_2 = Q_1 - Q_2 \newline~ V^\prime = \frac{q_1 + q_2}{C_1 + C_2}}
$$
然后把 $V^\prime$ 带回即可.

22.4 电能存储 Electric Energy Storage

最终公式

$$
\displaylines{U = \frac{1}{2} C V^2}
$$

存储在 capacitor 中的能量和用来 charge 它所做的功的一样多.

给一个 capacitor 充电就是将电子从一个极板移动到另一个极板.

capacitor 不是瞬间充好电，需要一定的时间.

从 $C = \frac{Q}{V}$ 可以看出，一个极板上的 $Q$ 越大，将一个电子一到极板另一侧所需的能量 $V$ 也就越大 (毕竟 $C$ 是常数，和 $Q$，$V$ 无关)

能量公式推导

$$
\displaylines{dW = V dq \newline~ V = \frac{q}{C} \newline~ W = \int V dq = \frac{1}{C} \int q dq = \frac{1}{2} \frac{Q^2}{C} \newline~ U = \frac{1}{2} \frac{Q^2}{C} \newline~ Q = CV \newline~ U = \frac{1}{2} \frac{Q^2}{C} = \frac{1}{2}CV^2\newline~}
$$

将能量存储在电容中视为存储在电场中

更好的理解能量存储在电容中是将其看作存储在电场中.

公式推导

$$
\displaylines{V = Ed \newline~ C = \frac{\epsilon_0A}{d} \newline~ U = \frac{1}{2}CV^2 =\frac{1}{2} \frac{\epsilon_0A}{d} E^2 d^2 = \frac{1}{2} \epsilon_0 E^2 A d \newline~}
$$
$A$ 是面积，$d$ 是极板间的距离，因此 $Ad$ 可以看作体积. 除开体积之后得到的就是能量密度:
$$
u = energy_density = \frac{1}{2} \epsilon_0 E^2
$$
这里的 $\epsilon_0A$ 是真空下的介电常数.

22-5 电介质 Dielectrics

Dielectrics 指的是 capacitor 中间的填充物.

Dielectrics 会影响 capacitance 的大小，影响的程度为常数 $K$ 表示, $\epsilon$ 是引入的新的 quantity, 成为物质的 permittivity (电介常数，也就是电介质的常数), 而 $\epsilon_0$ 是电介质为真空时的电介常数.

介电常数是一个相对值，以真空中为基准，是1 .
$$
\displaylines{C = K C_0 \newline~ C_0 = \epsilon_0 \frac{A}{d} \newline~ C = K \epsilon_0 \frac{A}{d} \newline~ \epsilon = K \epsilon_0 \newline~ C = \epsilon \frac{A}{d}}
$$
$C_0$ 是当填充物为真空时的 capacitance.

由于电容 $C$ 的变化而导致其他物理量的变化为, 原有的量为 $C_0$, $Q_0$, $V_0$, $E_0$

1. V 不变, Q的变化

$$
\displaylines{C = \frac{Q}{V} \newline~ C = K C_0 \newline~ Q = K Q_0}
$$

2. Q 不变, V 的变化

$$
\displaylines{C = \frac{Q}{V} \newline~ C = K C_0 \newline~ V = \frac{V_0}{K}}
$$

3. Q 不变, E 的变化

$$
\displaylines{C = \frac{Q}{V} \newline~ C = K C_0 \newline~ V = \frac{V_0}{K} \newline~ \newline E = \frac{V}{d} \newline~ \newline E = \frac{V_0}{Kd} = \frac{E_0}{K}}
$$

22-6 介电常数分子层面的描述 Molecular Description of Dielectrics

解释为什么在电极板间插入 Dielectrics 之后 capacitance 会增大 (都是变大).

书上的四幅图: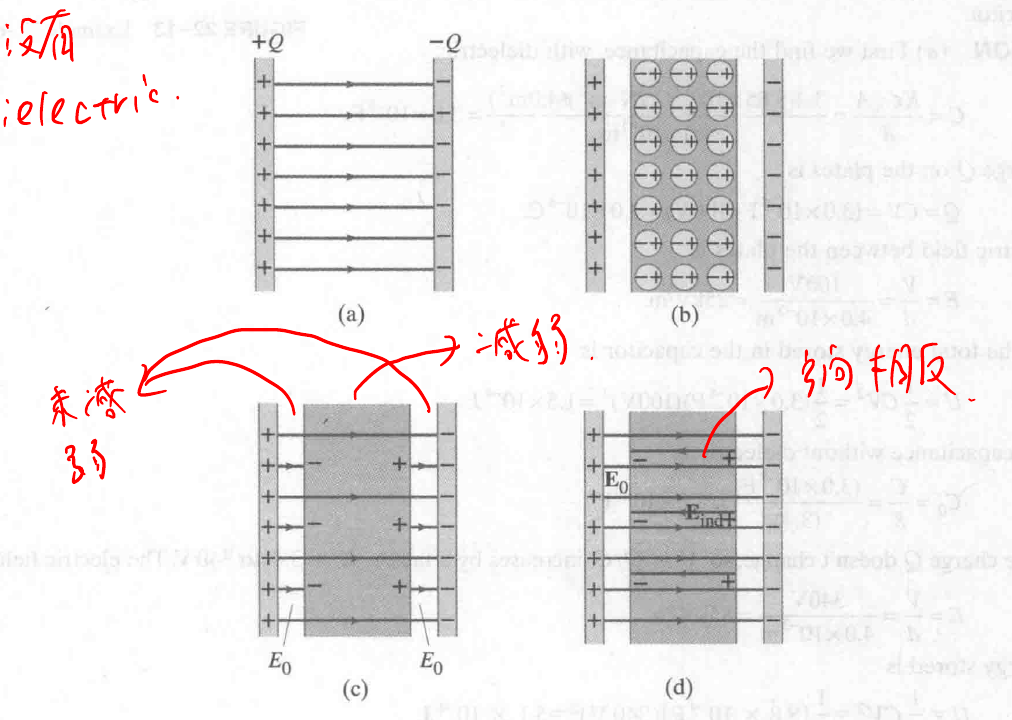

解析

图 a 是没有放入 Dielectrics 的电场示意图.

图 b 是放入了，由于 permanent dipole moment 的影响，物质内的分子一开始并不是像这样排列整齐的，而外部电场的作用使其整齐排列，负极朝向极板的正极.

从图 c 可以看出，部分电场线没有穿过 Dielectrics, 也就是说电场线数量减少，电场变小，

同时, 从图 d 看出，没有电场线穿过的部分，其内部形成了与原电场反向的电场，这是一个感应电场.

这里电场减小的 factor 假设为 K.

公式推导

$$
\displaylines{E = \frac{E_0}{K} \newline~ \newline V_0 = E_0 d \newline~ \newline V = Ed \newline~ \newline V = \frac{V_0}{K} \newline~ \newline C = K C_0}
$$

关于几个感应量 $E_{ind}$, $\sigma_{ind}$, 和 $Q_{ind}$ 的公式推导, $\sigma$ 是 charge density

$$
\displaylines{E = E_0 - E_{ind} = \frac{E_0}{K} \newline~ \newline E_{ind} = E_0(1 - \frac{1}{K}) \newline~ \newline E = \frac{\sigma}{\epsilon_0}, E_0 = \frac{\sigma_0}{\epsilon_0} \newline~ \newline \sigma_{ind} = \sigma(1 - \frac{1}{K}) \newline~ \newline \sigma = \frac{Q}{A} \newline~ \newline Q_{ind} = Q(1- \frac{1}{K})}
$$

Chapter 23 电流和电阻 Electric Currents and Resistance

灯丝发光的过程

移动的电子和原子发生碰撞. 导致电线中电能转化为热能, 灯丝温度上升发光🌟.

23.1 电池 The Electric Battery

一个电池将其他形式的能转化为电能.

最简单的 电芯 (electric cell) 包括:

• 两端为不同的金属 (一侧可为碳), 称为 电极 (electrodes)
• 一端电极所浸泡的溶液, 称为 电解质 (electrolyte).

几个 electric cell 连在一起就叫电池 (battery)做

未浸泡在溶液中的电极称为端子 (terminal)

端子间的电压取决于电极的材料以及其溶解的相对能力.

23.2 电流 Electric Current

当有电势差时, 就能够产生电流.

平均电流计算

$$
\displaylines{\overline{I} = \frac{\Delta Q}{\Delta t}}
$$

电流定义式

$$
\displaylines{I = \frac{dQ}{dt}}
$$

单位为 $1C/s = 1A$, 即 Ampere.

理解中正电荷流动的方向和电子流动的反方向等价.

23.3 欧姆定理: 电阻和电阻器

公式内容

$$
\displaylines{R = \frac{V}{I}}
$$

23.4 电阻率 Resistivity

发现,金属导线的电阻 和其:

• 长度 l
• 横截面积 A

有关, 即:

$$
\displaylines{R = \rho \frac{l}{A}}
$$

这里的 $\rho$ 为 电阻率 (resistivity), 只由材料本身决定. 单位为 $\Omega \cdot m$. 其值在某种程度上依赖于湿度, 温度, 和其他因素.

电阻率的倒数称为 电导率 $\sigma$ (conductivity) :

$$
\displaylines{\sigma = \frac{1}{\rho}}
$$
单位为 $(\Omega \cdot m)^{-1}$

和温度相关的电阻率

总体来说, 金属的电阻随温度升高而升高. (此时原子移动速度更快, 更加无序, 更容易干扰电子的流动)

如果温度变化不是太大, 金属电阻率几乎随温度线性增长:

$$
\displaylines{\rho_T = \rho_0[1 + \alpha(T - T_0)]}
$$
( $\rho_0$ 是参考温度 $T_0$ 下的电阻率. $\rho_T$ 是温度 $T$ 下的电阻率, $\alpha$ 是温度电阻率系数, 不同材料这个系数不同)

半导体的温度电阻率系数为负数, 因此, 温度上升, 其电阻降低. (这个系数本身似乎也和温度有关)

23.5 电能 Electric Power

公式为:

$$
\displaylines{P = \frac{dU}{dt} = \frac{dq}{dt} V \newline~ \newline
P = IV}
$$
单位为 watt ( $1W = 1J/s$)

推导式为

$$
\displaylines{P = IV \newline~ \newline
= I(IR) = I^2 R \newline~ \newline
= ( \frac{V}{R})V = \frac{V^2}{R}}
$$

千瓦时 (kilowatt-hour, kWh) 换算:

$$
\displaylines{1 kWh = (1000W)(3600s) = 3.60 \times 10^6J}
$$

23.6 交流电 Alternating Current

直流电, direct current, DC , 电流不改变方向.

交流电, alternating current, AC , 电流会改变方向. (其平均电流为 0)

电流为正弦图像, 如:

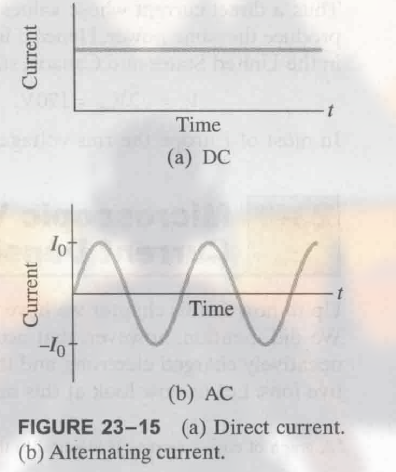
对于电压有:

$$
\displaylines{V = V_0 \sin 2\pi ft = V_0 \sin \omega t}
$$
( $V_0$ 指 peak voltage, 有 $\omega = 2 \pi f$ 即, 角频率, 含义为正弦波出现的频率)

对于电流有:

$$
\displaylines{I = \frac{V}{R} = \frac{V_0}{R} \sin \omega t = I_0 \sin \omega t}
$$
( $I_0$ 是 peak current.)

对于功率有:

$$
\displaylines{P = I^2 R = I^2_0 R \sin^2 \omega t \newline~ \newline
\overline{P} = \frac{1}{2}I_0^2 R = \frac{1}{2} \frac{V_0^2}{R}}
$$

电流和电压的均方根为:
$$
\displaylines{\overline{I^2} = \frac{1}{2} I_0^2 \newline~ \newline
\overline{V^2} = \frac{1}{2} V_0^2 \newline~ \newline
I_{rms} = \sqrt{\overline{I^2} = \frac{I_0}{\sqrt{2}} \newline~ \newline
V_{rms} = \sqrt{\overline{V^2} = \frac{V_0}{\sqrt{2}}}
$$

23.7 微观视角下的电流; 电流密度和漂移速度 Microscopic View of Electric Current: Current Density and Drift Velocity

最终式子为:

$$
\displaylines{I = \sum_i n_i q_i v_{di} A}
$$
( $n_i$ 为单位体积内的电子数, $q_i$ 为电子的带电量, $v_{di}$ 为电子的漂移速度, $A$ 为电线的横截面积)

只是在静电场中, 导体内部的电场才为零.

电流密度 (current density, $j$), 定义了 单位面积的电流大小, 即:

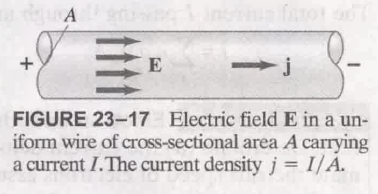
如果电线横截面上的电流密度相等 (均匀分布), 则有:

$$
\displaylines{j = \frac{I}{A}\ or\ I = jA}
$$

如果电线横截面上的电流密度不均匀, 则有:

$$
\displaylines{I = \int j \cdot dA}
$$

某一点电流密度的方向为该点处正电荷的受力方向. (即 $j$ 的方向和电场强度 $E$ 方向相同)

可以想象, 原本自由电子在导体中高速向随机方向运动, 加上一个电场后, 电子会受到电场力的作用然后开始加速, 最终达到的速度称为 漂移速度 (drift velocity, $v_d$) (比原来的速度或大或小, 常常比平均随机速度小得多)

计算一段时间通过截面的总电荷量

假设电流 $I$ 速度为 $v_d$, 在时间 $\Delta t$ 内, 通过的距离为 $v_d \Delta t$, 电线的横截面为 $A$, 则电流流过的体积为 $Y = Al = A v_d \Delta t$, 如果单位体积中的电子数为 $n = N/V$ (N 为总电子数), 则在时间 $\Delta t$ 中通过截面的总电荷量为:

$$
\displaylines{ \Delta Q = (nV) (-e) = -(nAv_d \Delta t)(e)}
$$

因此电流又可以定义为:

$$
\displaylines{I \frac{\Delta Q}{\Delta t} = -neA v_d}
$$

电流密度 $j = I/A$ 又可以定义为:

$$
\displaylines{j = -nev_e}
$$

通用形式为:

$$
\displaylines{j = \sum_i n_i q_i v_{di} \newline~ \newline
I = \sum_i n_i q_i v_{di} A}
$$

电子的 drift velocity 慢并不代表电流的速度慢. (把看作水流, 一侧流出, 另一侧已经流入)

结合一些公式的推导式

通过:

$$
\displaylines{R = \rho \frac{l}{A} \newline~ \newline
I = jA \newline~ \newline
V = El \newline~ \newline
V = IR \newline~ \newline
得: El = (jA) (\rho \frac{l}{A}) = jpl \newline~ \newline
j = \frac{l}{\rho}E = \sigma E}
$$
(这里电场为匀强电场)

23.8 超导 Superconductivity

在温度极低时, 某些金属或某些混合物或某些合金的 电阻率变为零. 这种状态就称为 超导 (superconductivity)

Chapter 24 直流电路 DC Circuits

24.1 电动势和端电压 EMF and Terminal Voltage

将其他形式的能转换为电能的装置称为 电动势的源 (a source of electromotive force or emf) (虽然叫 electromotive force, 但这个量并不是力)

在电路中没有电流时, 一个源两端的电势差叫做这个源的emf. 用符号 $\mathcal{E}$ 表示.
(也就是说, 电路中没有电流时的电源的端电压就是电动势, 而当电路中有电流时, 由于内阻会分压, 此时电源电压加上内阻的电压才为电动势, 比如说, 一个 12-V 的电池, 那么这个电池的电动势就是 $12V$)

电势能反应电子的位置.

电池本身的电阻称为 内阻 (internal resistance) , 常用 $r$ 表示.

从一个示例来看:

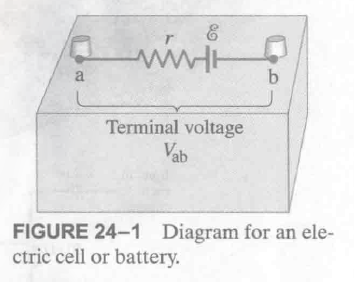
这里 $V_{ab}$ 为 $a,b$ 两端的端电压, 当电路中没有电流时有:

$$
\displaylines{V_{ab} = \mathcal{E}}
$$

当电路中有电流 $I$ 时, 有:

$$
\displaylines{V_{ab} = \mathcal{E} - Ir}
$$

大部分情况下是将内阻忽略不计, 然后端电压直接等于电源电压.

24.2 串联电阻和并联电阻 Resistors in Series and in Parallel

电阻串联

$$
\displaylines{R_{eq} = R_1 + R_2 + R_3}
$$

电阻并联

$$
\displaylines{ \frac{1}{R_{eq}} + \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}
$$

24.3 基尔霍夫定律

见电分.

24.4 RC 电路 Circuits Containing Resistor and Capacitor

见电分.

Chapter 25 磁 Magnetism

“Magnets” 这一名称的由来: 人们在 Asia Minor 下一个叫 Magnesia 的地方发现能相互吸引的石头，就把这些石头用发现地命名为 “Magnets”

25-1 磁和磁场 Magnets and Magnetic Field

Magnets 一般有两种形状:

• bar, 条状
• horseshoe, 马蹄状

对 Magnets 的 N 极 (North)和 S 极 (South) 的定义:

• 指向地理上的北极的一侧称为 N 极
• 指向地理上的南极的一侧称为 S 极

暂时不存在只有一个磁极的磁铁. 一个磁铁分为两截后同样会同时具有 N 极和 S 极。

每个物体都有磁性，但是强度不同。

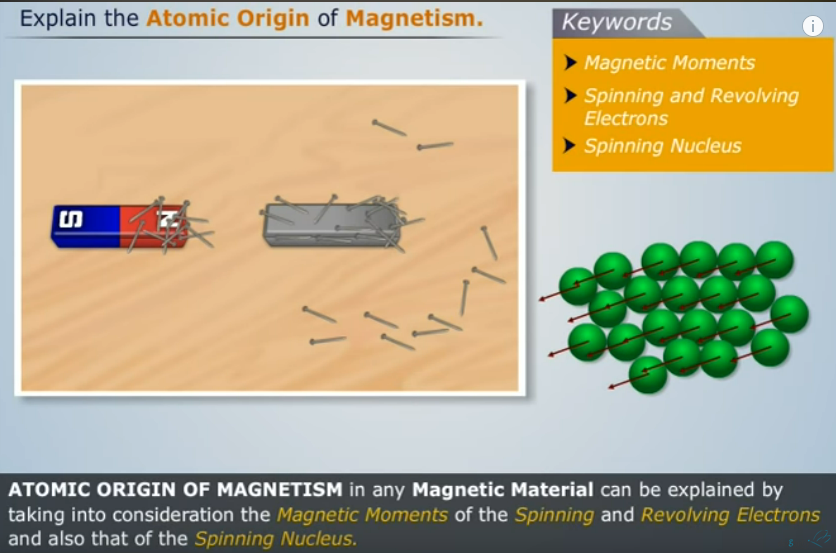
磁性的由来

参考知乎1

磁场的产生可以分为两种:

• 运动电流 (变化的电场产生磁场)
• 基本粒子的自旋 (自旋的时候也是产生电流, 进而产生磁场)

所有物质都有磁性，只是大小不同.

浅显的认知: 不容易被磁化的物质，其内部的原子难以受外部磁场的影响而排列整齐.

磁力的存在是由于磁场.

参考 YouTube

质子和电子的自旋:

自旋和电子绕核旋转都会产生电流:

如这张图，这三个磁场向量合向量就是这个粒子的磁场方向.

同一方向

如果所有的粒子的磁场向量都位于一个方向: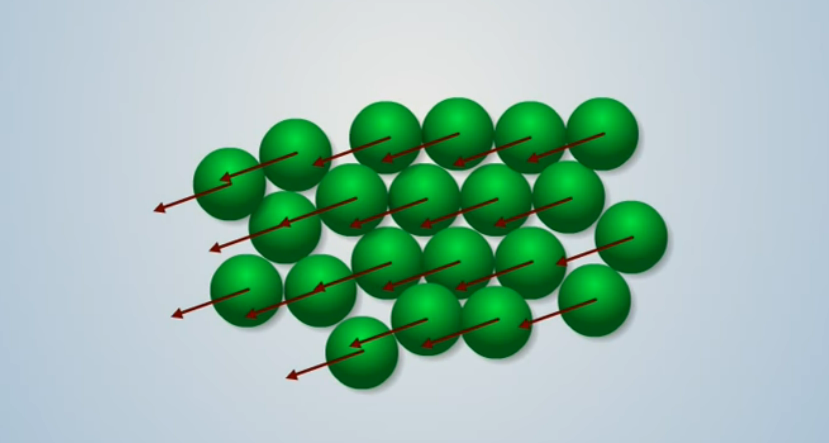

那么其合向量就很大. 物体就会表现出磁性.

不同方向

如果各个粒子的向量方向不同，那么就会有狠多被抵消掉:

物体的磁性就不会表现出.

施加外部磁场

施加一个外部磁场，可能使物体内粒子产生的磁场向量方向排列整齐，这也是为什么铁块在靠经一块磁铁使就具有了磁性:

相关数学公式

磁场线

方向的定义:

磁场线的方向是在磁场中，小磁针 N 极转动的方向.

磁场线的密集程度和磁场强度成正比.

在磁铁外部，磁场线总是从 N 极发出并回到 S 极. 且始终是一个闭合的曲线.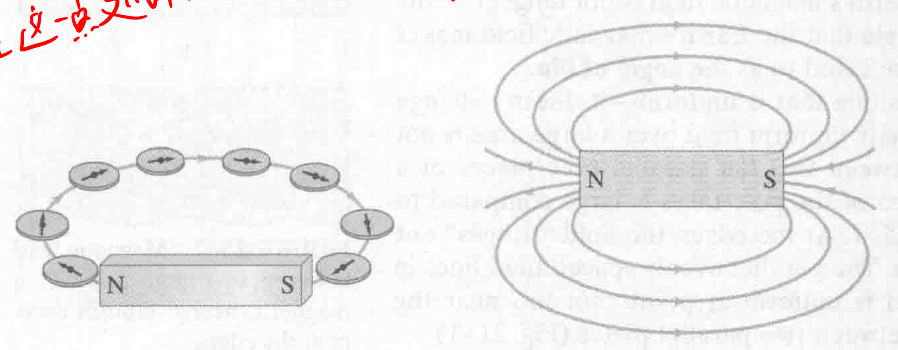

形成完美的 uniform field 的并不容易，但是当:

• 磁极表面远大于两个磁极之间的距离

可以近似得到一个 uniform field.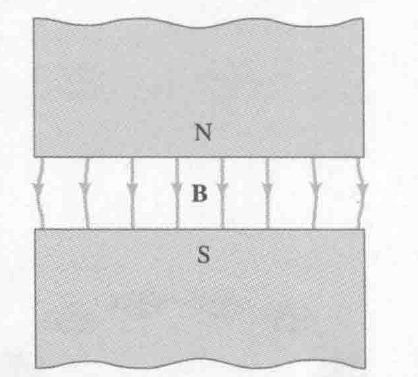

25-2 电生磁 Electric Currents Produce Magnetism

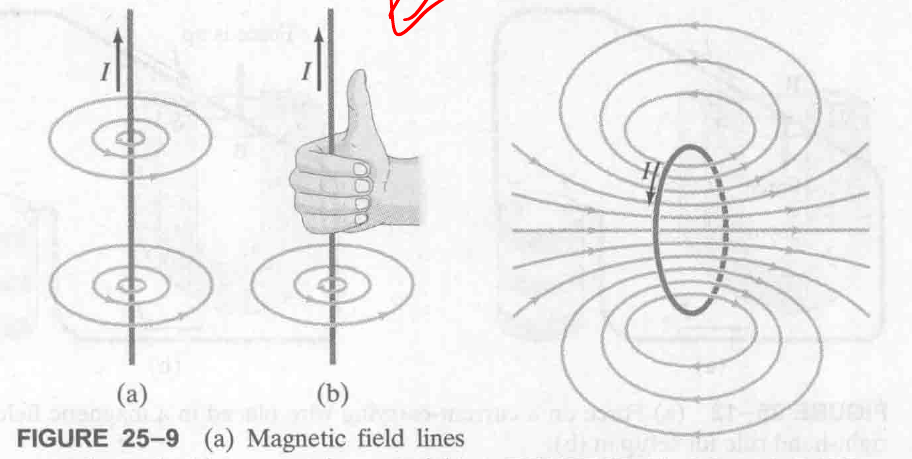
用右手定则根据电流的方向判断生成的磁场的方向.

有两种情况:

• electric current in a straight wire
• a circular loop of wire

25-3 在磁场中电流所受到的力; B 的定义 Force on an Electric Current in a Magnetic Field; Definition of B

从小磁针转动可以知道，其受到了一定力的作用.

力的方向与电流方向和磁场方向都垂直, 也可以用右手定则判断, 拇指方向为力的方向:

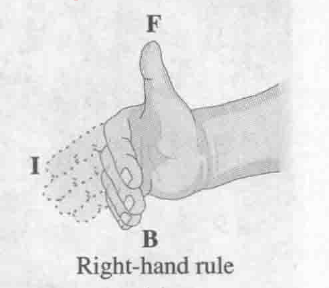
注意电流方向和磁场方向都用四指判断.

计算公式推导

首先有观察到这样一个关系:
$$
F \propto IlB \sin \theta
$$
然后:
$$
\displaylines{F = IlB \sin \theta \newline~ \newline F = Il \times B}
$$
后者为向量形式， $l$ 和 $B$ 是向量。和 $\sin$ 相关的都可以改为叉乘，且可以用右手定则判断方向.

更加通用的形式:
$$
dF = I dl \times B
$$

B 的定义

可以看作是磁感线的密集程度，单位面积穿过的磁感线数量. 其大小在 26 章描述

SI 单位是 Tesla (T), $T = 1N/A \cdot m$.

地球表面的磁场强度为 $0.5 \times 10^{-4}T$.

两个表示 B 方向的符号:

向外 point out

向里 point inward

25-4 在磁场中移动的电子受到的力 Force on an Electric Charge Moving in a Magnetic Field

公式推导, 已知在时间 t 内穿过 N 个带电量为 q 的粒子

$$
\displaylines{I = \frac{Nq}{t} \newline~ \newline l = vt \newline~ \newline F = Il \times B \newline~ \newline F = \frac{Nq}{t} vt \times B \newline~ \newline F = Nqv \times B}
$$
那么一个粒子受到的力就为:
$$
F = qv \times B
$$

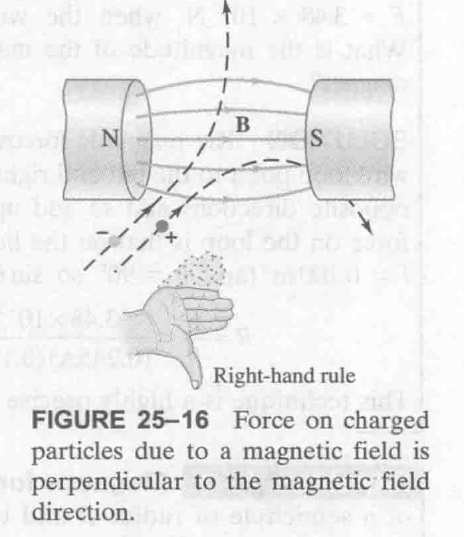
力的方向判断, 这里的 $v$ 是粒子运动方向, 因此用右手定则判断

拇指方向为力的方向, 四指为粒子运动方向 (不是电流方向). 注意粒子的电性会影响最终的结果.

在均匀磁场中

做匀速圆周运动，且不做功 (力的方向和运动方向垂直)

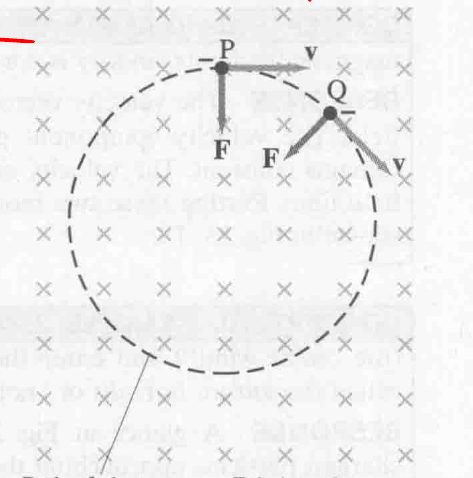
结合圆周运动的相关公式推导

$$
\displaylines{F = ma \newline~ \newline a = \frac{v^2}{r} \newline~ \newline F = qvB = \frac{mv^2}{r} \newline~ \newline r = \frac{mv}{qB} \newline~ \newline T = \frac{2 \pi r}{v} \newline~ \newline T = \frac{2 \pi m}{qB}}
$$

当速度方向和磁场方向不垂直时的路径为 Spiral Path: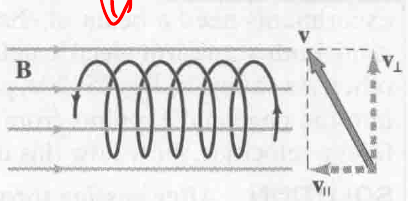

同时位于磁场和电场中

Lorentz equation:

$$
F = q(E + v \times B)
$$

25-5 环形电路中的力矩; 磁偶矩 Torque on a Current Loop; Magnetic Dipole Moment

观察这幅图, 其中 和 是力的方向, 这里的 torque 也是电压表等器材指针转动的原理:

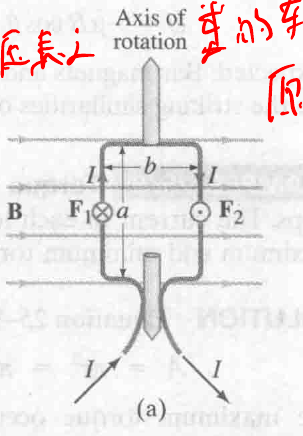
公式推导

$$
\displaylines{\tau = l_1 \times F \newline~ \newline l_1 = \frac{b}{2} \newline~ \newline F = Il_2 \times B \newline~ \newline l_2 = a \newline~ \newline \tau = \frac{b}{2} I a B + \frac{b}{2} I a B = Iab B \newline~ \newline A = ab \newline~ \newline \tau = IA B}
$$
可以看出 $ab$ 是线圈的面积. 如果线圈有 N 轧:
$$
\tau = N IA B = N IA B
$$

如果线圈和磁场不是垂直的，磁场强度 B 会变化如: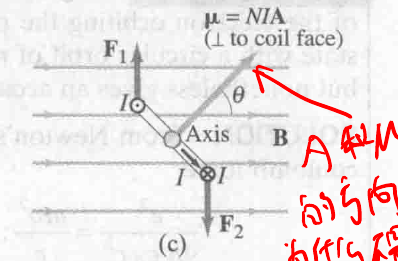

此时 $\tau$ 变为:
$$
\tau = NIAB \sin \theta
$$
$\theta$ 为小角 ( $0^\circ ~ 90^\circ$ ).

为了将 $\tau$ 的计算式写成两个物理量相乘的形式, 定义了一个物理量 magnetic dipole moment 电偶矩:
$$
\mu = NIA
$$

最终，torque 的表达式可以写为:
$$
\tau = \mu \times B
$$

利用 $\tau$ 和 角度 $\theta$ 计算做功为:
$$
U = \int \tau d\theta = \int NIAB \sin \theta d\theta = -\mu B \cos \theta + C
$$

一般我们选取 $\theta = 90^\circ$ 也就是磁场和线圈垂直为初始点，即 $U = 0$, 就可以算出:
$$
\displaylines{U = 0 = -\mu B \cos \theta + C = 0 + C \newline~ \newline C = 0 \newline~ \newline \therefore U = -\mu B \cos \theta = -u \cdot B}
$$

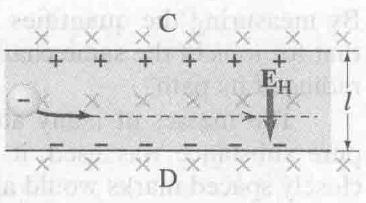
25-8 霍尔效应 The Hall Effect

The Hall Effect 描述了，当一个电子在存在磁场和电场的环境下运动时，其速度到达一定值，使得电场力和洛伦兹力 (洛伦兹力其实就是磁力, 只不过其描述的是一个电子所受的磁力) 相等.

$$
\displaylines{F = eE \newline~ \newline F = ev \times B \newline~ \newline eE = evB \newline~ \newline E = vB}
$$

此时的电势差被称为 Hall emf ($\xi$):
$$
\displaylines{\xi = El = vBl}
$$

Chapter 26 磁场的源 Source of Magnetic Field

这里主要讲电生磁.

26-1 直线电线中的电流产生的磁场 Magnetic Field Due to a Straight Wire

实验观察出的现象:
$$
\displaylines{B \propto \frac{I}{r}}
$$
也就是说，电流越大，其产生的磁场越大，离电流越远，磁场越小.

在这种 Straight Wire 产生的磁场，其计算公式为 (通用计算式要结合后面的 Ampere’s law):
$$
\displaylines{B = \frac{\mu_0}{2 \pi} \frac{I}{r}}
$$

其中 $\mu_0$ 是一个常量，称为 permeability of free space, 值为 $4 \pi \times 10^{-7} T \cdot m/A$

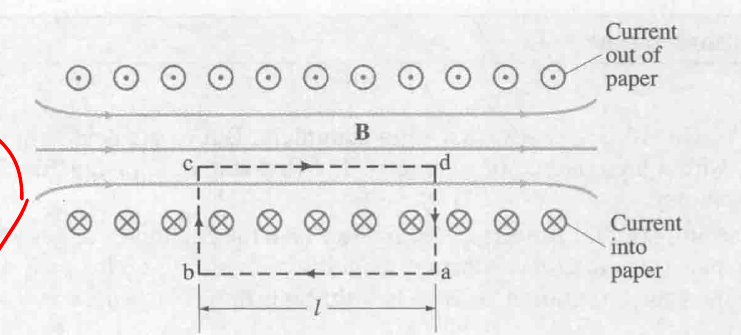
26-2 两个平行导线间的力 Force between Two Parallel Wires

同向相吸, 异向排斥.

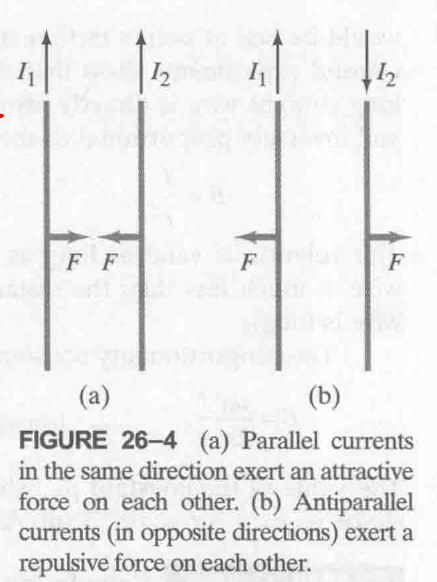
施加的力大小相等方向相反.

公式推导

$$
\displaylines{B_1 = \frac{\mu_0}{2 \pi} \frac{I_1}{r} \newline~ \newline F = I_2B_1l = \frac{F}{l} = \frac{\mu_0}{2 \pi} \frac{I_1 I_2}{d}}
$$

26-3 安培和库仑的定义 Operational Definition of the Ampere and the Coulomb

26-4 Ampere’s Law

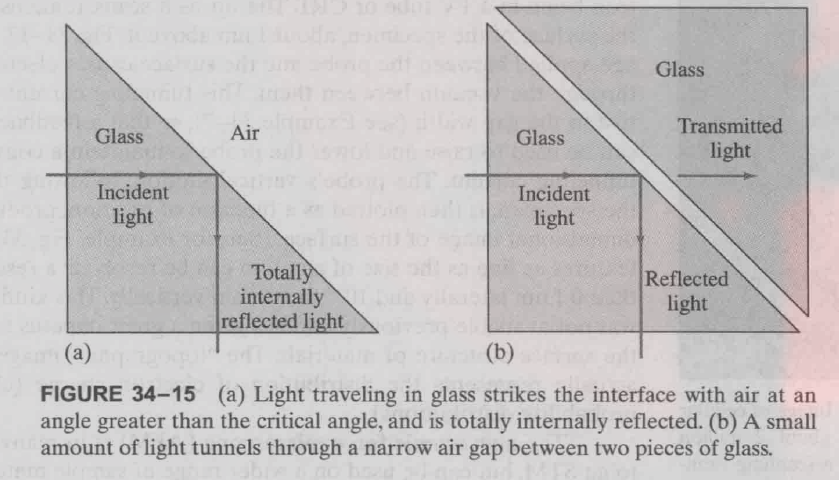
安培定理是用来计算, 电流产生的磁场大小. 其限制是只能作用在闭合曲线.

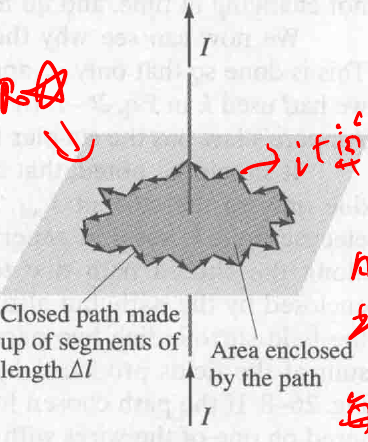
Ampere’s law 运用积分的概念，将路径划分为极小份，然后相加得到:
$$
\displaylines{\sum B \Delta l = \mu_0 I_{encl} \newline~ \newline \int B \cdot dl = \mu_0 I_{encl}}
$$

书中并没有给出为什么磁场强度 $B$ 乘以长度 $dl$ (积分后就是面积), 的结果是 $\mu_0 I$

这里每一点的 B 都不相同，因此主要是靠右式计算. 也可以看出，其实和高斯定理一样，选取合适的路径即可计算，一般选取圆，上述图形的计算其实和下面一样.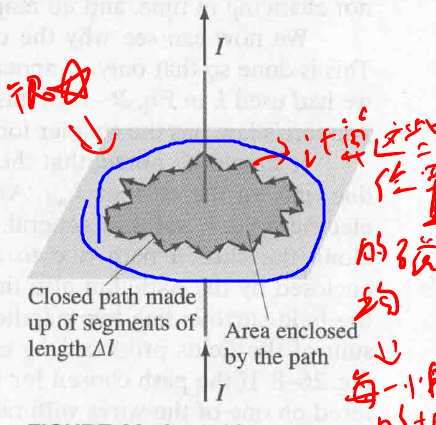

此时再回头推导之前计算 Straight Wire 产生的磁场强度.

推导过程

$$
\displaylines{\int B \cdot dl = B \int dl = B(2 \pi r) = \mu_0 I_{encl} \newline~ \newline B = \frac{\mu_0 I}{2 \pi r}}
$$

26-5 螺线管和环形线圈产生的磁场 Magnetic Field of a Solenoid and a Toroid

solenoid 示意图

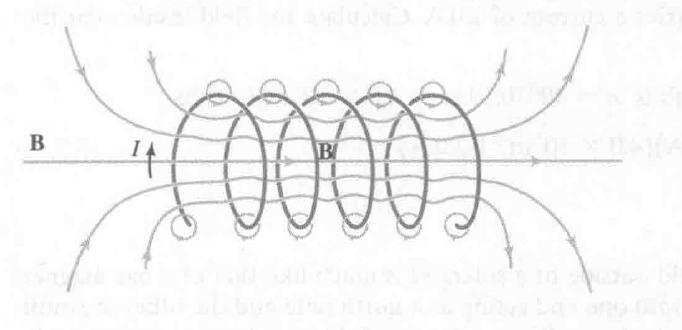
一个长线绕了很多圈.

螺线管内部的磁场较强，外部相对于内部非常小

从上图可以看出，产生外部磁场的部分为: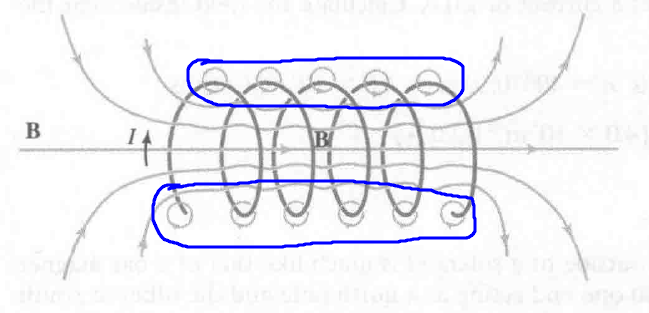

公式推导

$$
\displaylines{\oint B \cdot dl = \int_a^b B \cdot dl + \int_b^c B \cdot dl +\int_c^d B \cdot dl +\int_d^a B \cdot dl \newline~ \newline = \int_c^dB \cdot dl \newline~ \newline = Bl \newline~ \newline \oint B \cdot dl = N \mu_0 I \newline~ \newline Bl = N \mu_0 I \newline~ \newline n = \frac{N}{l} \newline~ \newline B = \mu_0 n I}
$$
其中 bc 边和 ad 边抵消，ba 边太小而被忽略.

n 的单位长度的圈数. 可以看出，solenoid 内的磁场强度和线圈数和电流大小有关.

Toroid

Toroid 示意图

其外形像把 solenoid 折成一个环.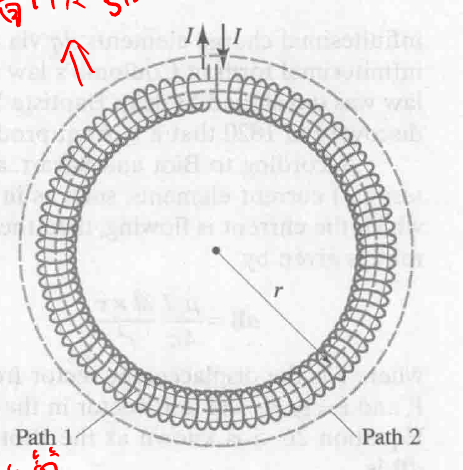

内部磁场公式推导

还是看上面那一幅图，结合 Ampere’s law, 选取的面为 Path1 由虚线标识:
$$
\displaylines{\oint B \cdot dl = \mu_0 I_{encl} \newline~ \newline B(2 \pi r) = \mu_0NI \newline~ \newline B = \frac{\mu_0 NI}{2 \pi r}}
$$

特点:

• 外部磁场为零

推导

选取的为 Path2, 对于每一个环如图:

左右流过的电流大小相等，方向相反，合电流因此为 0, 结合 Ampere’s law:
$$
\displaylines{\oint B \cdot dl = \mu_0 I_{encl} \newline~ \newline B (2 \pi r) = 0 \newline~ \newline B = 0}
$$

Path1 相当于选取的是:

26-6 毕奥萨伐尔定律 Biot-Savart Law

用于计算 $dl$ 即一小段电流产生的磁场对距离为 $r$ 处的强度. 而 Ampere’s law 需要闭合曲线.

书中也没有给出这个公式的证明过程.

和 Coulomb’s Law 结合记忆:

Coulomb’s law

$$
\displaylines{dE = \frac{1}{4 \pi \epsilon_0} \frac{dq}{r}}
$$

Biot-Savart’s law

$$
\displaylines{dB = \frac{\mu_0 I}{4 \pi} \frac{dl \times \hat{r}}{r^2}\newline~ \newline
(这里的 \hat{r} 只是表示方向, 模长为 1) \newline~ \newline
dB = \frac{\mu_0 I dl \sin \theta}{4 \pi r^2} \newline~ \newline B = \int dB}
$$

注意这是 $r^2$, 结合库仑定理记忆.

26-8 电磁和螺线管 Electromagnets and Solenoids

可以把 solenoids 视作一个磁铁, 一侧被看作是 north pole, 另一侧为 south pole.

26-9 磁性物质中的磁场; 滞后现象 Magnetic Field in Magnetic Materials; Hysteresis

在一个 Toroid 中加入铁之后，总的磁场强度为:
$$
\displaylines{B_0 = \mu_0 n I \newline~ \newline B = B_0 + B_M = \mu nI}
$$
(毕竟加入铁之后磁场强度会变大, 且一般情况下 $B_M >> B_0$)
上面的 $\mu$ 被称为 magnetic permeability.

对于 ferromagnetic (铁磁) 材料而言， $\mu$ 要远大于 $\mu_0$ ( $\mu_0$ 如何得出的)

Chapter 27 电磁感应和法拉第定律 Electromagnetic Induction and Faraday’s Law

27-1 感应电动势 Induced EMF

Faraday 发现，恒定的磁场不会产生电流，只有变化的磁场才能产生电流.

总结为

An induced emf is produced by a changing magnetic field

27-2 法拉第感应定律和楞次定律Faraday’s Law of Induction; Lenz’s Law

磁场变化越快，induced emf 越大, 也就是和变化率有关 (这里是 $\phi_B$ 即 flux 的变化率).

求 $\phi_B$ flux 的公式

$$
\displaylines{\phi_B = B_\perp A = BA \cos \theta = B \cdot A \newline~ \newline \phi_B = \int B \cdot dA}
$$

当面积作为向量时, 其方向垂直于平面.

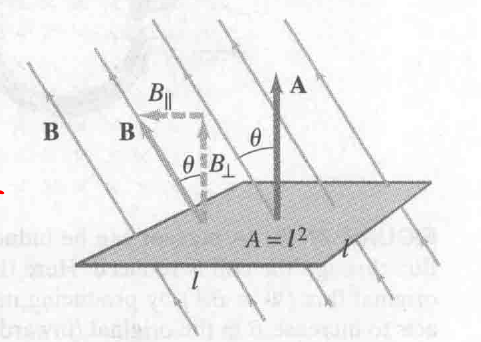
$\phi$ flux 可以看作是 total number of lines passing through the loop. 单位可以从公式中看出，为 tesla-meter$^2$, 即 weber, $1 Wb = 1 T \cdot m^2$

Faraday’s Law of induction

$$
\displaylines{\xi = - \frac{d \phi_B}{dt} \newline~ \newline \xi = -N \frac{d \phi_B}{dt}}
$$

为什么是负数，这就涉及到 Lenz’s Law.

Lenz’s Law

An induced emf gives rise to a current whose magnetic field opposes the original change in flux.

也就是阻碍变化. 即如果 flux 增大，那么感应的则会是反方向，如果 flux 减小，那么感应的会是同方向.

27-3 移动导体中的感应电动势 EMF Induced in a Moving Conductor

导体棒移动, 公式推导

$$
\displaylines{\xi = \frac{d \phi_B}{dt} = \frac{B dA}{dt} = \frac{Blv dt}{dt} = Blv}
$$

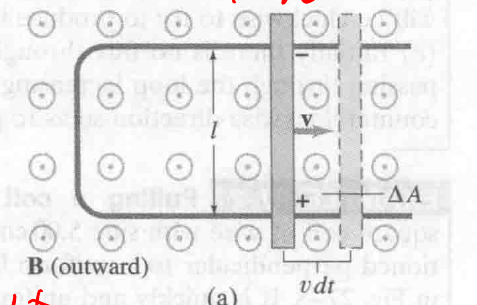
导体棒受力公式推导

$$
\displaylines{F = IlB \newline~ \newline I = \frac{\xi}{R} \newline~ \newline \xi = Blv \newline~ \newline I = \frac{Blv}{R} \newline~ \newline F = IlB = \frac{B^2 l^2}{R} v }
$$

27-4 变化磁通量产生电场 A Changing Magnetic Flux Produces an Electric Field

Faraday’s Law – General Form

$$
\displaylines{V_{ab} = \int_a^b E \cdot dl \newline~ \newline \xi = \oint E \cdot dl \newline~ \newline \oint E \cdot dl = - \frac{d \phi_B}{dt}}
$$

如果力是 conservative force, 如这里的电场力，那么:
$$
\displaylines{ V_{ab} = V_a - V_b = \int_a^b E \cdot dl \newline~ \newline \oint E \cdot dl = 0}
$$

尽管静电场是 conservative fields, 但是变化磁场产生的电场是 nonconservative field.

Chapter 28 电感和电磁波 Inductance; and Electromagnetic Oscillations

28-1 互感 Mutual Inductance

不管是互感系数还是自感系数，都只和导体本身有关，如形状，面积. 与引起感应现象的电流无关.

Inductance 这个量用来描述，电流的变化会引起的 $\phi_B$ flux 的变化是多少.

互感示意图

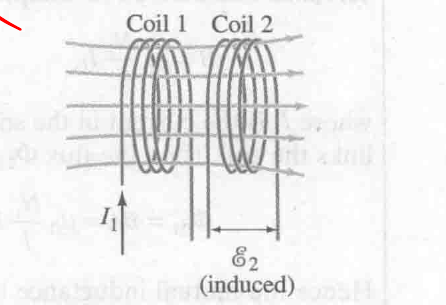
Mutual inductance, 从名字就能看出，至少需要两个导体.

Inductance 计算公式

$$
\displaylines{M_{21} = \frac{N_2 \phi_{21}}{I_1}}
$$

(虽然这里有 $I$, 但其值实际上与电流无关, 下面有推导)

表明 Inductance 和电流 I 无关的公式推导

借助这道题目:

$$
\displaylines{B = \mu_0 \frac{N_1}{l} l_1 \newline~ \newline \phi_{21} = BA = \mu_0 \frac{N_1}{l} I_1 A \newline~ \newline M = \frac{N_2 \phi_{21}}{I_1} = \frac{\mu_0 N_1 N_2 A}{l}}
$$

用 Inductance 计算 emf 的公式推导 (也就是 emf 和互感的关系式)

$$
\displaylines{M_{21} = \frac{N_2 \phi_{21}}{I_1} \newline~ \newline \xi_2 = - N_2 \frac{d \phi_{21}}{dt} \newline~ \newline \xi_2 = - M_{21} \frac{dI_1}{dt}}
$$

Mutual inductance 的单位是 henry (H), 从公式可以看出，为 $1 H = 1 V \cdot s/A = 1 \Omega \cdot s$

Mutual inductance 可用来传递能量.

28-2 自感 Self-Inductance

和 mutual inductance 有一点区别，这里是一个 solenoid (可能也不是 solenoid), 它自身的变化引起自身线圈产生感应电流.

Self-Inductance 计算公式

$$
\displaylines{L = \frac{N \phi_B}{I}}
$$

同样可以推导出其大小与电流无关, 这里以一个 solenoid 为例

$$
\displaylines{B = \mu_0 nl \newline~ \newline n = \frac{N}{l} \newline~ \newline \phi_B = BA = \frac{\mu_0 NIA}{l} \newline~ \newline L = \frac{N \phi_B}{I} = \frac{\mu_0 N^2 A}{l}}
$$

利用自感和 Faraday’s law 计算 emf

$$
\displaylines{ L = N \frac{\phi_B}{I} \newline~ \newline \xi = -N \frac{d \phi_B}{dt} = - L \frac{dI}{dt}}
$$

从公式可以看出, $L$ 越大，反向的 emf 就越大, $I = \frac{V}{R}$, 就会变小，因此inductance 可以充当电阻使用.

28-3 存储在磁场中的能量 Energy Stored in a Magnetic Field

让感应电流达到 I 所消耗的能量就是 inductance 所存储的能量.

公式推导，当 inductance L 中电流的变化速率为 $ \frac{dI}{dt}$ 时

$$
\displaylines{P = I \xi = L I \frac{dI}{dt} \newline~ \newline dW = P dt = L I di \newline~ \newline W = \int dW = \int_0^I L I dI = \frac{1}{2} L I^2 \newline~ \newline U = \frac{1}{2} L I^2}
$$

写成磁场的形式，这和载体有关，这里是一个 solenoid:
$$
\displaylines{L = \frac{\mu_0 N^2 A}{l} \newline~ \newline U = \frac{1}{2} L I^2 = \frac{1}{2} ( \frac{\mu_0 N^2 A}{l}) (\frac{Bl}{\mu_0 N})^2 = \frac{1}{2} \frac{B^2}{\mu_0}Al \newline~ \newline \mu = \frac{1}{2} \frac{B^2}{\mu_0}}
$$

$\mu$ 是能量密度 ($Al$ 就是体积).

与存储在电场中的能量结合记忆:

电场中

$$
\displaylines{\mu = \frac{1}{2} \epsilon_0 E^2}
$$

磁场中

$$
\displaylines{\mu = \frac{1}{2} \frac{B^2}{\mu_0}}
$$

Chapter 29 麦克斯韦方程组和电磁波 Maxwell’s Equations and Electromagnetic Waves

电磁场波可以穿过空间.

麦克斯韦将所有的电和磁现象统一到一个理论中.

场的概念由法拉第引出.

所有的电和磁现象都可以用四个包含电场和磁场的方程描述, 这些方程被称为 麦克斯韦方程组 (Maxwell’s equations).

可以把电场理解为单位面积里的电场线数量.

把磁场强度理解为单位面积里的磁感线数量.

29.1 变化的电场产生磁场; 安培定理和位移电流 Changing Electric Fields Produce Magnetic Fields; Ampere’s Law and Displacement Current

这里开始讲原来的安培定理的不足部分.

安培定理, 电流产生磁场

$$
\displaylines{\oint B \cdot dl = \mu_0 I_{encl}}
$$

本节结论

$$
\displaylines
{
\oint B \cdot dl = \mu_0 (I + I_D)_{encl} \newline~ \newline
where \newline~ \newline
I_D = \epsilon_0 \frac{d \Phi_E}{dt}
}
$$

正式论述

这里不是很明白, 说的是, 如图:

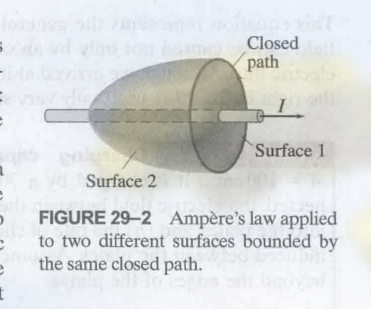
在 Surface 1 上应用安培定理和在 Surface 2 上应用安培定理等价 (?, 可能是 Surface 1 和 Surface 2 结合是一个封闭图形)

又说, 如图:

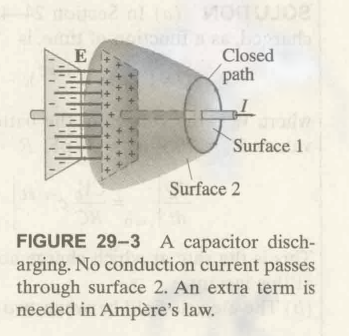
这是一个电容在放电, 此时, 安培定理对 Surface 1 仍然有效, 但对 Surface 2 无效 (?, 可能是此时 Surface 1 和 Surface 2 结合不是一个封闭图形), 没有传导电流流经 Surface 2, 因此安培定理右侧为零, 但此时电线周围有磁场, 即方程左端不为零, 因此出现矛盾.

麦克斯韦解决这个问题的方法为, 他认为安培定理还需要一个额外的参数, 包含此时电场的变化.

这个参数的推导

电容 $C$ 两侧的电荷量为 $Q$, 有:

$$
\displaylines
{
Q = CV
}
$$

$V$ 是此时电容两侧的电势差, 同时:

$$
\displaylines
{
V = Ed \newline~ \newline
C = \frac{\epsilon_0 A }{d}
}
$$
(d 是两极板间的距离, $A$ 是极板的面积)

最终有:

$$
\displaylines
{
Q = CV = (\epsilon_0 \frac{A}{d}) (Ed) = \epsilon_0 AE
}
$$

如果此时电荷量的变化率为 $dQ/dt$, 有:

$$
\displaylines
{
\frac{dQ}{dt} = \epsilon_0 A \frac{dE}{dt}
}
$$

而通过电流的定义可知, $dQ/dt$ 也能表示电流, 因此:

$$
\displaylines
{
I = \frac{dQ}{dt} = \epsilon_0 A \frac{dE}{dt} = \epsilon_0 \frac{d \Phi_E}{dt}
}
$$
其中 $\Phi_E = EA$, 也就是电通量.

因此安培定理最终可以写为:

$$
\displaylines
{
\oint B \cdot dl = \mu_0 (I_{encl} + I_{extra}) \newline~ \newline
\oint B \cdot dl = \mu_0 I_{encl} + \mu_0 \epsilon_0 \frac{d\Phi_E}{dt}
}
$$

这个额外的电流往往非常小, 不容易在实验中测得.

位移电流

麦克斯韦把这个额外的电流称为 位移电流 $I_D$ (displacement current) . 普通的电流就被称为 传导电流 (conduction current) , 因此安培定理还可以写成:

$$
\displaylines
{
\oint B \cdot dl = \mu_0 (I + I_D)_{encl} \newline~ \newline
where \newline~ \newline
I_D = \epsilon_0 \frac{d \Phi_E}{dt}
}
$$
(实际上, 位移电流既不代表一个电荷的流动, 也没有位移, 这个名字极具误导性)

习题

the rate of charge of electric field between the plates 的求法:

$$
\displaylines
{
E = \frac{\sigma_0}{d} = \frac{Q/A}{d}
}
$$

应用安培定理时, 有 $dl$, 因此需要找出题中关于周长的信息, 比如半径, 形状.

29.2 高斯磁力定律 Gauss’s Law for Magnetism

也就是高斯定理在磁场中的形式.

结论为:

$$
\displaylines
{
\oint B \cdot dA = 0
}
$$

具体论述

磁场 $B$ 和 磁通量 $\Phi_B$ 的关系为:

$$
\displaylines
{
\Phi_B = \int B \cdot dA
}
$$

当面积是一个封闭的曲线时, 穿过这个表面的磁通量就可以写为:

$$
\displaylines
{
\Phi_B = \oint B \cdot dA
}
$$

高斯定理在电场中的形式为:

$$
\displaylines
{
\oint E \cdot dA = \frac{Q}{\epsilon_0}
}
$$

由于没有单磁极的磁体, 高斯定理在磁场中的形式为 :

$$
\displaylines
{
\oint B \cdot dA = 0
}
$$
(毕竟有多少磁感线进入, 就有多少磁感线放出)

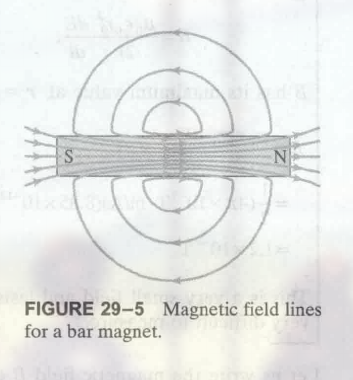
29.3 麦克斯韦方程组 Maxwell’s Equations

麦克斯韦方程组是:

• 高斯定理
• 法拉第定律
• 安培定理
  的结合:

$$
\displaylines
{
\oint E \cdot dA = \frac{Q}{\epsilon_0}\ \ (高斯定理电场中的形式, 封闭曲线内电荷产生的电场) \newline~ \newline
\oint B \cdot dA = 0\ \ (高斯定理磁场中的形式, 封闭曲线内磁体产生的磁场) \newline~ \newline
\oint E \cdot dl = - \frac{d\Phi_B}{dt}\ \ (法拉第定理, 磁生电) \newline~ \newline
\oint B \cdot dl = \mu_o I + \mu_0 \epsilon_0 \frac{d \Phi_E}{dt}\ \ (安培定理, 电生磁)
}
$$
(两个面积分, 和两个线积分)

可以用一句话概括:

1. 将电场和它的源(电荷)关联起来的库仑定律通用形式
2. 将磁场和它的源(磁体)关联起来的库仑定律通用形式
3. 变化的磁场产生电场
4. 变化的电场产生磁场

29.4 电磁场的产生 Production of Electromagnetic Waves

麦克斯韦从, 一个变化电场会在一个空地 (指没有介质) 产生一个磁场, 衍生出另一个结论.

变化磁场产生变化电场, 变化电场又产生变化磁场, and so on.

他最终得出, 这些变化的场是由电场和磁场组成的可以传播的波, 即 电磁波 (electromagnetic wave)

将两个棍子看作是发射天线:

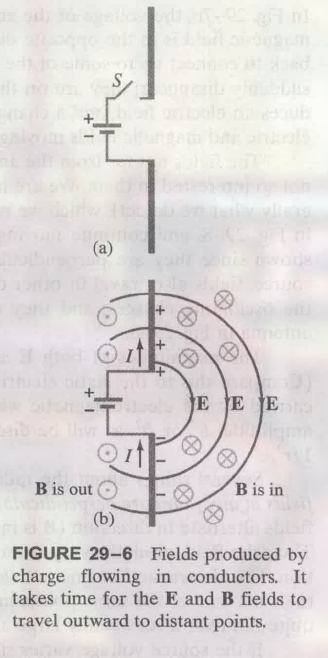
当电源接通时, 和正极相连的 rod 迅速带上正电, 和负极相连的 rod 迅速带上负电, 这里的 $E$ 旁边的箭头表明两个极板间的电场线, 由于电流, rod 两侧也就形成了磁场. 比如这里左侧为 out (指向纸外), 右侧为 in (指向纸内).

注意 , 这里并不是接通的回路, 因此负极损失的电子不会得到补充.

开关打开后电场和磁场 (电场和磁场是同时产生的) 就开始传播了. 但此时为 直流电 , 电流大小不会变化, 因此生成稳定的磁场, 也就不会继续生成变化的电场.

当电源为交流电时, 有:

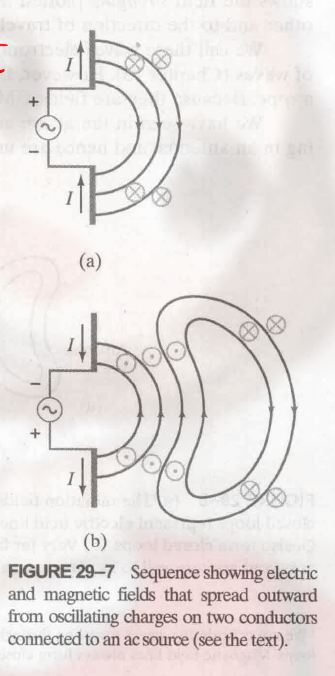
(这时电子能来回流动)

此时由于两极板间的电场是变化的, 极板两侧会产生磁场.

图 $(b)$ 中最右侧的指向纸内的磁场就是之前图 $(a)$ 时发出的. 由于老旧两个电场方向相反, 恰好形成了一个闭环. (远端的闭环就是一段时间前发出的电磁波, 近端的为此时发出的)

传播在离天线近的场被称为 近场 (near field) , 此处不关心这部分, 因为过于复杂. 传播在离天线远的场被称为 辐射场 (radiation field) .

垂直于电子振荡方向的场强最大 , 振荡方向的 场强为 0 .

发现, 在辐射场中的 $E$ 和 $B$ 的大小随距离减小的幅度为 $1/r$.电磁波携带的能量 和 $E^2$ 或 $B^2$ 成正比. 因此波的强度 deceases as $1/r^2$

从下图可以看出:

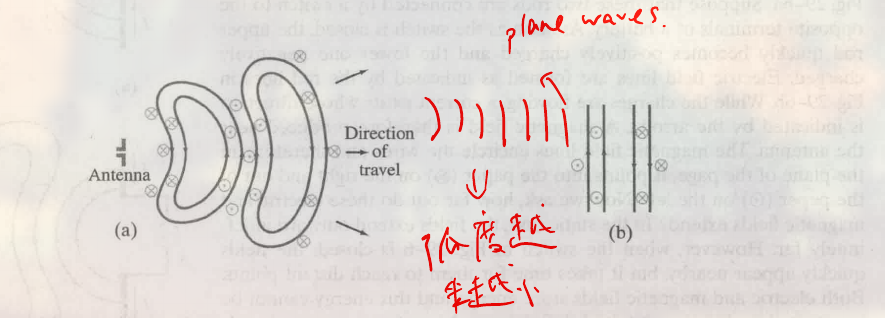
1. 磁场方向和电场方向始终垂直
2. 场的方向在改变, 磁场和电场是 in place 的, 即同时变为 0 或同时变为 maximum
3. 在传递很远的距离后, 场线变得平缓, 此时称为 平面波 (plane wave)

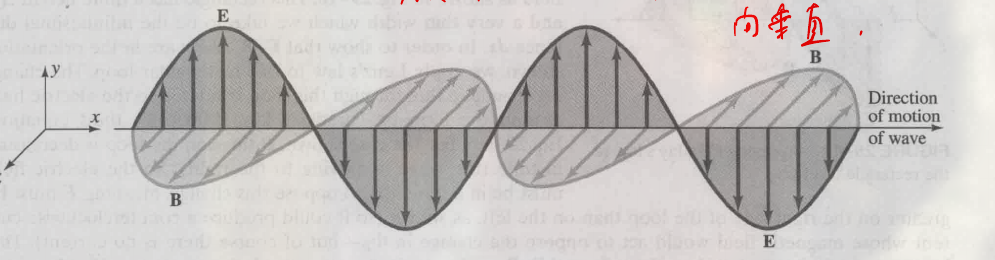
我们把这些波称为 电磁波 electromagnetic (EM) waves , 其为 横波 (transverse wave), 即传播方向和振动方向垂直. 电磁波是场波而不是物质波 (?), 由于其为场, 其可以传播到 empty space (指没有介质的空间)

电磁波示意图为:

理解电磁波

参考 B 站 1

扭结 (kink) 的理解, 当电荷加速时, 新电场和旧电场之间会出现扭结:

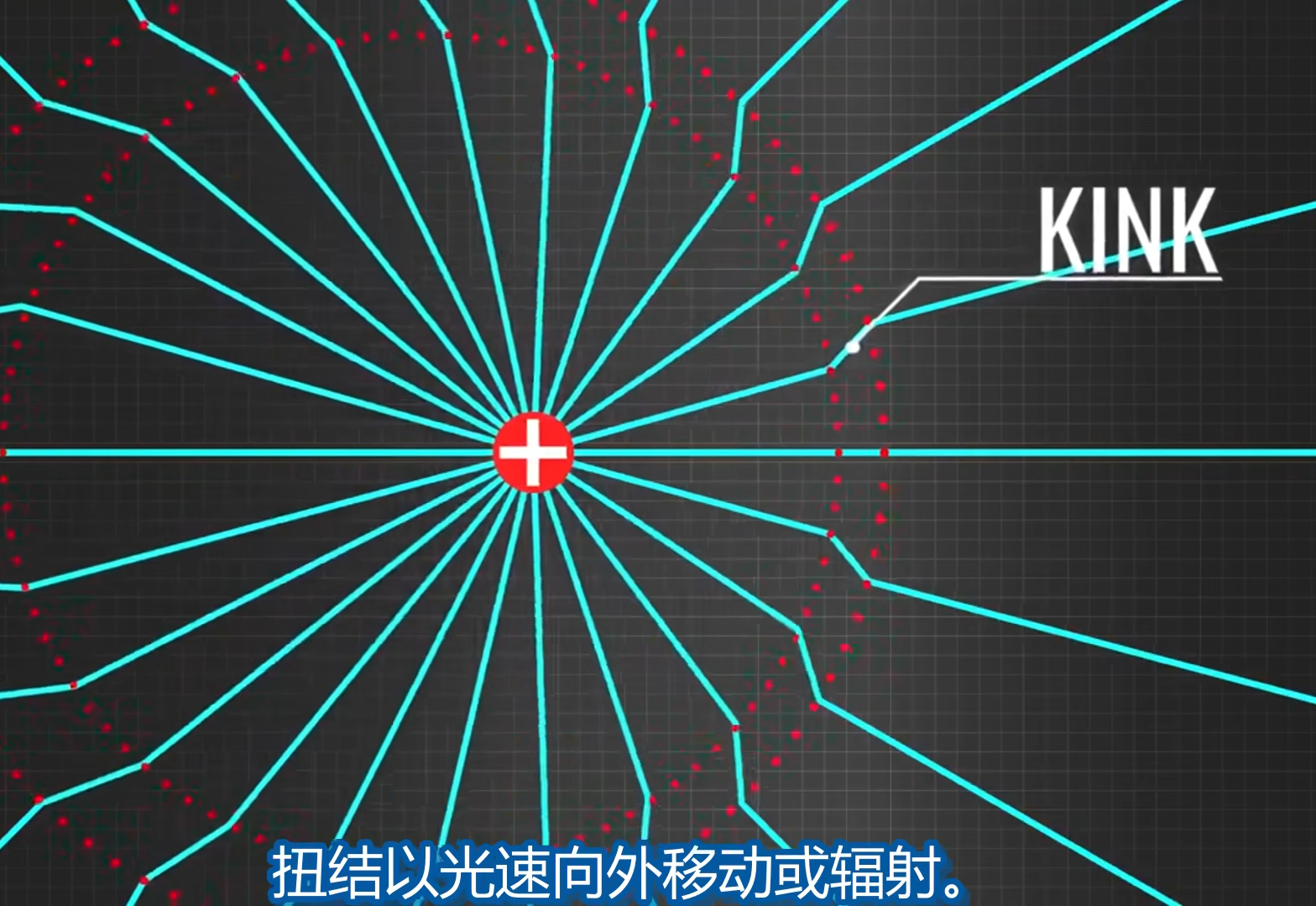
(加速前电荷产生一个电场, 其覆盖了很大范围, 也可以说传播了很大范围, 此时电荷加速, 此时会形成一个新的场, 旧场过渡到新场之间的连接就称为 kink)

扭结以光速向外移动或扩散.

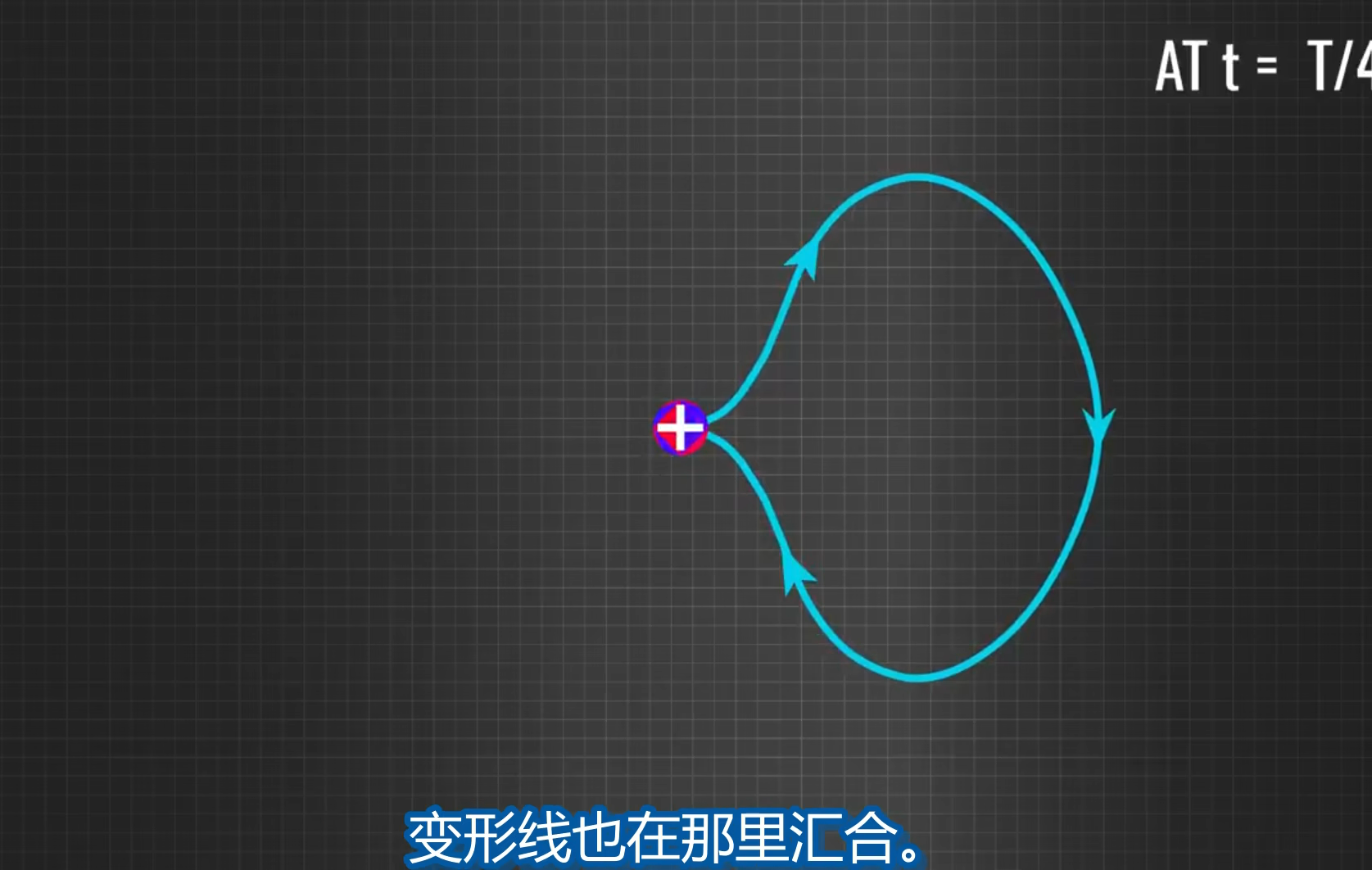
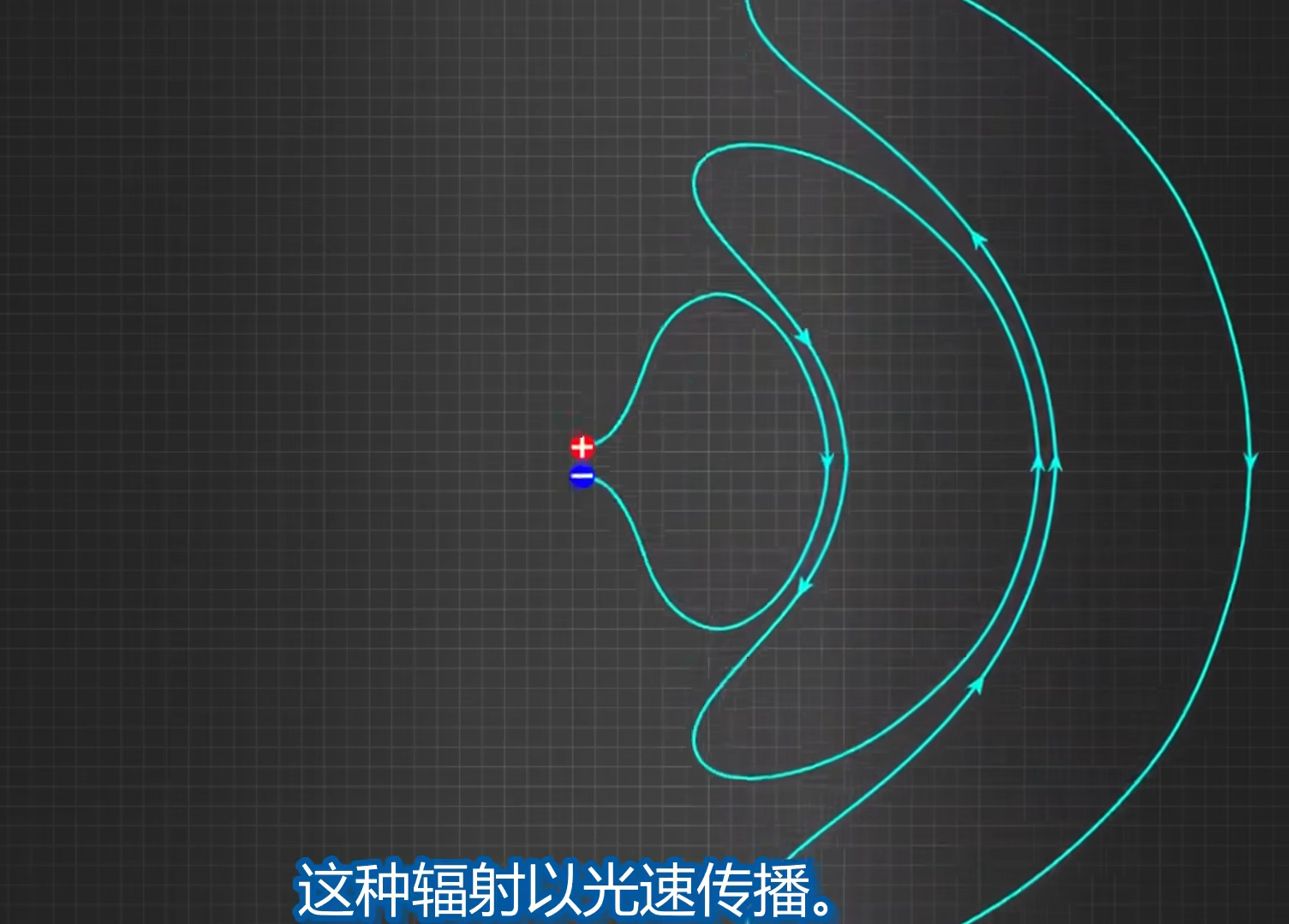
如图, 有正负两个电荷, 等同于电偶, 好像叫电偶振荡, 其运动特点为, 向中间靠近时加速, 向两边时减速, 也就是说, 在中间位置两电荷速度最大, 即电场变化得最快 (因为电场的大小是由两电荷的距离决定的, 速度最大时两电荷的距离变化最快, 因此电场变化最快, 此时位于波峰波谷), 到两侧时电荷速度为零, 即电场变化为 0 (表示电场最小, 变化率为 0 而不是电场为 0):

电荷的加速和减速会形成扭结 (变形线), 而当两电荷在中心点会合时, 变形线也在这里会合:

然后脱落并散发光:

这种辐射以光速传播:

如果施加电场强度变化, 就是一个正弦波:

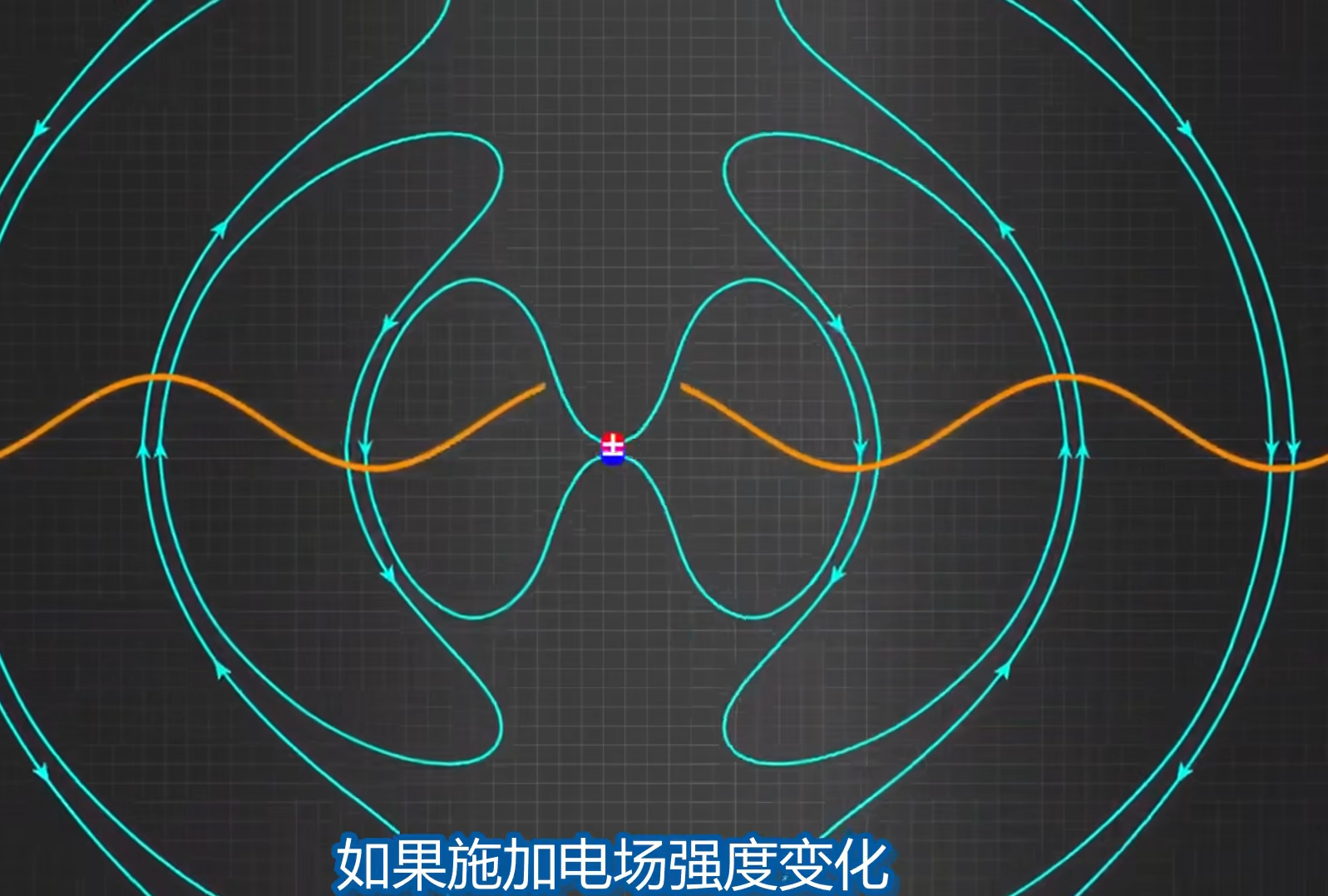
而这种变化的电场会产生变化的磁场 (垂直于电场)

29.5 从麦克斯韦方程中得到电磁波及其速度 Electromagnetic Waves, and Their Speed, from Maxwell’s Equations

考虑一个 free space (没有电荷和任何传到电流, 意思是距离产生波的源很远处), 使得电磁波在传递到很远距离后能变为 平面波 (plane wave) (意味着在任何时刻, E 和 B 都均匀分布在很大的范围)

假设一个坐标系, 波的传播在 x 方向且速度为 $v = vi$, $E$ 和 y 轴平行, B 和 z 轴平行 如:

由于 $Q = I = 0$, 此时的麦克斯韦方程组变为:

$$
\displaylines
{
\oint E \cdot dA = 0\ \ (由于\ \frac{Q}{\epsilon_0} = 0 ) \newline~ \newline
\oint B \cdot dA = 0\ \ ( 本身就为0 ) \newline~ \newline
\oint E \cdot dl = - \frac{d\Phi_B}{dt} ( 其与 I/Q 无关 )\newline~ \newline
\oint B \cdot dl = \mu_0 \epsilon_0 \frac{d \Phi_E}{dt}\ \ ( 由于\ \mu_0 I = 0 )
}
$$

如果波是正弦波, 且波长为 $\lambda$, 频率为 $f$, 则有:

$$
\displaylines
{
E = E_y = E_0 \sin(kx - \omega t) \newline~ \newline
B = B_y = B_0 \sin(kx - \omega t) \newline~ \newline
where\ \newline~ \newline
k = \frac{2 \pi}{\lambda},\ \omega = 2 \pi f,\ and\ f\lambda = \frac{\omega}{k} = v
}
$$

有:

$$
\displaylines
{
\frac{E}{B} = v
}
$$
的关系式 (书上推导不是很懂)

最终得出

$$
\displaylines
{
v^2 = \frac{1}{\mu_0 \epsilon_0}
}
$$
( $\mu_0$ 指磁导率, $\epsilon_0$ 指电介常数, 可以看出其传播速度和介质有关)

在真空中的传播速度为:
$$
\displaylines
{
v = 3.00 \times 10^8 m/s
}
$$

29.6 光作为电磁波以及电磁频谱

麦克斯韦在计算出电磁波速度的基础上, 认为光是一种电磁波.

电磁波由 Heinrich Hertz 在 1887 年首次生成并检测. Hertz 使用了一个 spark-gap apparatus. Hertz 的实验是麦克斯韦理论的强有力的确认.

可见光的波长在十九世纪初被测出. 范围为 $4.0 \times 10^{-7}m \sim 7.5 \times 10^{-7}m$. (即 $400nm \sim 750nm$), 可见光的波长可以用:

$$
\displaylines
{
f \lambda = c
}
$$
( $f$ 是频率, $\lambda$ 是波长, $c$ 是光速)

来算出. 可见光的频率范围为 $4.0 \times 10^{14}Hz \sim 7.5 \times 10^{14}Hz$.

光根据频率的分类如下:

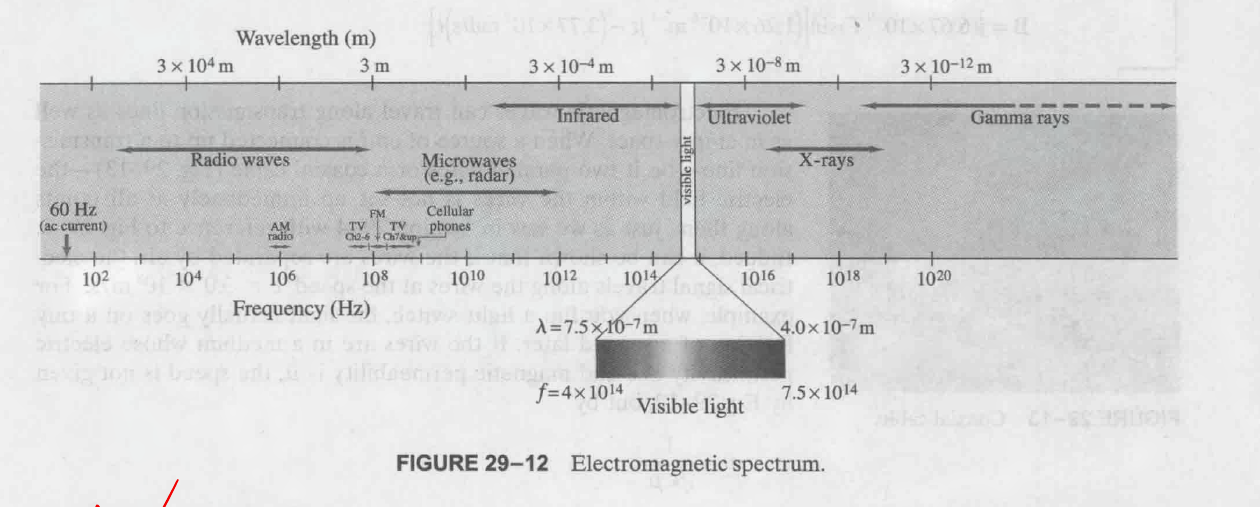
这个图被称为 电磁波图谱 (electromagnetic spectrum)

高频率的波难以用电子器材生成, 这些波一般在自然过程中生成, 如原子, 分子, 核子等的辐射

电磁波可以通过加速电子或其他带电粒子来产生. (如天线加速的电子)

X-ray 是由快速移动的电子撞击金属从而急剧减速产生.

红外线 (IR, infrared radiation, 频率比可见光低), 负责太阳射线中加热的部分.

我们的皮肤分子会合红外频率共振, 因此红外线会被优先吸收并使其发热.

如果电线介质的介电常数 (electric permittivity) 为 $\epsilon$, 磁导率 (magnetic permeability) 为 $\mu$, 则电磁波在其中的速度为:

$$
\displaylines
{
v = \frac{1}{\sqrt{\epsilon \mu}}
}
$$

29.7 电磁波中的能量; 坡印廷矢量 Energy in EM Waves; the Poynting Vector

电磁波能从一个地方携带能量到另一个地方. 能量大小和 moving 电场和磁场有关.

由于:

$$
\displaylines
{
\mu_E = \frac{1}{2} \epsilon_0 E^2 \newline~ \newline
(存储在电场中的能量, \mu_E 为单位体积中的能量) \newline~ \newline
\mu_B = \frac{1}{2} \frac{B^2}{\mu_0} \newline~ \newline
(存储在磁场中的能量, \mu_B 为单位体积中的能量)
}
$$

因此总能量为:

$$
\displaylines
{
\mu = \mu_E = \frac{1}{2} \epsilon_0 E^2 + \mu_B = \frac{1}{2} \frac{B^2}{\mu_0}
}
$$

可将其转换为只包含电场的式子或只包含磁场的式子:

$$
\displaylines
{
\sqrt{\epsilon_0 \mu_0} = \frac{1}{c} \newline~ \newline
B = \frac{E}{c} \newline~ \newline
\mu = \mu_E = \frac{1}{2} \epsilon_0 E^2 + \frac{1}{2} \frac{\epsilon_0 \mu_0 E^2}{\mu_0} \newline~ \newline
= \epsilon_0 E^2
}
$$

或:

$$
\displaylines
{
\mu = \epsilon_0 E^2 = \epsilon_0 c^2 B^2 = \frac{\epsilon_0 B^2}{\epsilon_0 \mu_0} \newline~ \newline
\mu = \frac{B^2}{\mu_0}
}
$$

或一个式子中包含 E 和 B:

$$
\displaylines
{
\mu = \epsilon_0 E^2 = \epsilon_0 E c B = \frac{\epsilon_0 E B}{\sqrt{\epsilon_0 \mu_0}} \newline~ \newline
\mu = \sqrt{ \frac{\epsilon_0}{\mu_0} }EB
}
$$

计算电磁波传播 per unit time per unit area 的能量

给出向量 S , 即 坡印廷矢量 (Poynting vector) (其方向为电磁波传播的方向, 单位为 $W/m^2$)

最终公式

$$
\displaylines
{
S = \frac{1}{\mu_0} (E \times B)
}
$$
(记忆技巧, 能量要么和 $E^2$ 和 $B^2$ 有关， 要么就是和 $EB$ 有关)

假设电磁波穿过面积为 $A$ 的区域 (垂直于 x 轴), 在时间 $dt$ 内, 波移动的距离为 $dx = cdt$, 此时在时间 $dt$ 内穿过 A 的能量就等同于穿过体积的能量, 有:

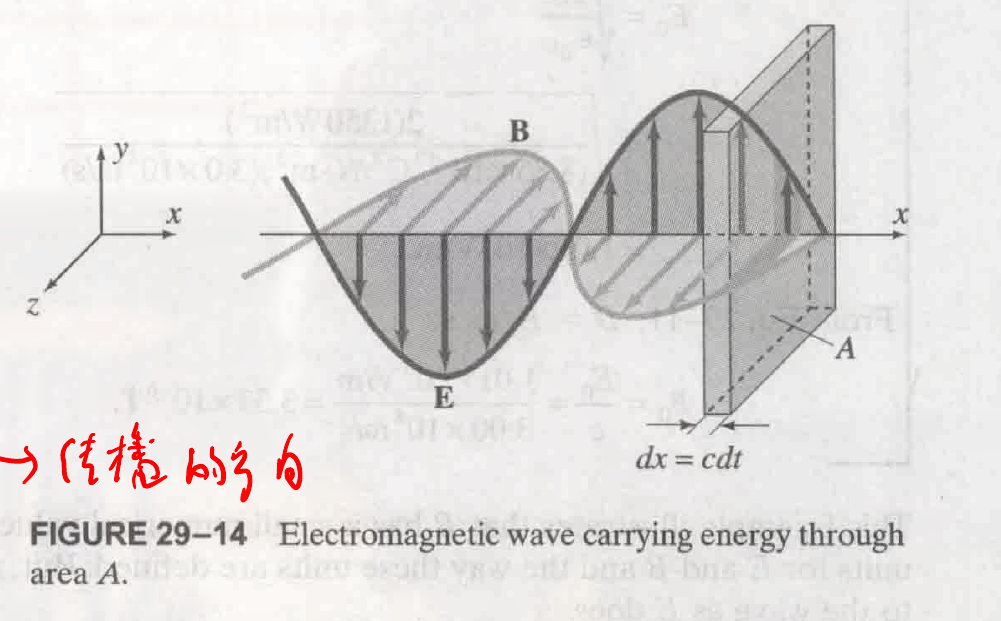
$$
\displaylines
{
dV = Adx = Ac dt \newline~ \newline
\mu = \epsilon_0 E^2 \newline~ \newline
dU = u dV = (\epsilon_0 E^2) (Ac dt) \newline~ \newline
S = \frac{1}{A} \frac{dU}{dt} = \epsilon_0 c E^2 \newline~ \newline
( \frac{1}{A} 指单位面积, \frac{1}{dt} 指单位时间 )
}
$$

也可以写为磁场或电场与磁场都有的形式:

$$
\displaylines
{
E = cB \newline~ \newline
c = \frac{1}{\sqrt{\epsilon_0 \mu_0}} \newline~ \newline
S = \epsilon_0 c E^2 = \frac{c B^2}{\mu_0} = \frac{EB}{\epsilon_0}
}
$$

由于 S 的方向垂直于 E 和 B 构成的面, 因此可以写成:

$$
\displaylines
{
S = \frac{1}{\mu_0} (E \times B)
}
$$

平均坡印廷矢量计算为:

$$
\displaylines
{
\overline{S} = \frac{1}{2} \epsilon_0 c E^2 = \frac{1}{2} \frac{c}{\mu_0} B_0^2 = \frac{E_0 B_0}{2 \mu_0}
}
$$

如果 E 和 B 是正弦函数, 则有:

$$
\displaylines
{
\overline{S} = \frac{E_{rms} B_{rms}}{\mu_0}
}
$$

29.8 辐射压 Radiation Pressure

考虑电磁波携带线性动量.

当电磁波撞击物体表面时, 其会被吸收或反弹, 由于动量传递 (F = dp/dt, 力就是单位时间内动量的变化), 此时会施加一个力的作用, 而单位面积受到的这个里的作用就称为 辐射压 (radiation pressure) .

如果电磁波被一个物体完全吸收, 那么传递的动量为:

$$
\displaylines
{
\Delta p = \frac{\Delta U}{c}
}
$$
(这个公式在相对论中有提到)

如果电磁波被一个物体 全部反射 , 此时传递的动量为:

$$
\displaylines
{
\Delta p = \frac{2 \Delta U }{c}
}
$$

若吸收了一部分, 反射了一部分, 则有:

$$
\displaylines
{
\Delta p = \frac{K \Delta U }{c} \newline~ \newline
1 \le k \le 2
}
$$

推导

全部吸收:

$$
\displaylines
{
F = \frac{dp}{dt} \newline~ \newline
\frac{dU}{dt} = \overline{S} A \newline~ \newline
P = \frac{F}{A} = \frac{1}{A} \frac{dp}{dt} = \frac{1}{Ac} \frac{dU}{dt} = \frac{\overline{S}}{c} \newline~ \newline
}
$$

全部反射:

$$
\displaylines
{
P = \frac{2 \overline{S}}{c}
}
$$

Chapter 32 相对论 Special Theory of Relativity

讨论几个非经典的结论, 运动参考系的 长度收缩 (length contraction) 和 时间膨胀 (time dilation)

主要记住

• 不同参考系的同时性不同, 即一个时间在一个参考系发生, 在另一个参考系下可能没有发生
• 速度越大, 长度越短
• 速度越大, 时间越慢

20 世纪之前的物理学称为 经典物理 (classical physics)

20 世纪之后的物理学称为 现代物理 (modern physics) , 主要是相对论和量子力学的发展.

狭义相对论和广义相对论分别指代的东西:

• 狭义相对论是指阿尔伯特·爱因斯坦在1905年提
  出的相对论，它描述的是物理定律在不同的参照系中的变化。
• 广义相对论则是1915年爱因斯坦提出的，它把时空和物质结合在一起，认为时空是可以扭曲的，而物质则受到时空的影响

32.1 伽利略-牛顿 相对论

爱因斯坦相对论改变的是观察不同参考系的方式.

在一个参考系中的长度, 在另一个参考系中可能不同.

在一个参考系中的时间, 在另一个参考系中可能不同.

狭义相对论处理的是惯性系 (inertial reference frames)的事件.

(惯性系指满足牛顿第一定律的参考系, 即不受外力的物体会保持静止或匀速直线运动)

旋转和其他加速参考系是非惯性系.

相对于一个惯性参考系匀速运动的参考系本身, 也是一个惯性参考系.

伽利略和牛顿认为的相对论: 基本的物理法则在所有的惯性参考系中相同.

伽利略和牛顿的相对论包括几个无法证明的假设. 其假设

• 物体在一个参考系中的长度和在另一个参考系中相同.
• 物体在一个参考系中时间流逝的速度和另一个参考系相同

在经典力学中, 时间和空间是绝对的, 即, 其测量值不会随参考系改变而改变. 物体的质量, 所受的作用力, 加速度都不受参考系影响. 因此, 牛顿第二定律 $F=ma$ 也满足其相对论. 表明 所有的惯性系都是相同的

牛顿-伽利略相对论出现问题 , 于麦克斯韦预测出了光速为 $3.00 \times 10^8m/s$, 其方程并没有显示光有相对速度. 因此科学家认为这里有一个特殊的参考系, 使得光速为 $3.0 \times 10^8m/s$

当时的科学家认为光传播在一个特殊的介质 ether (以太) 中, 并且假设以太渗透于所有空间. 认为麦克斯韦方程中的光速和以太相关.

事实证明麦克斯韦方程并不满足相对性原理.

很多实验都表明光的速度不变.

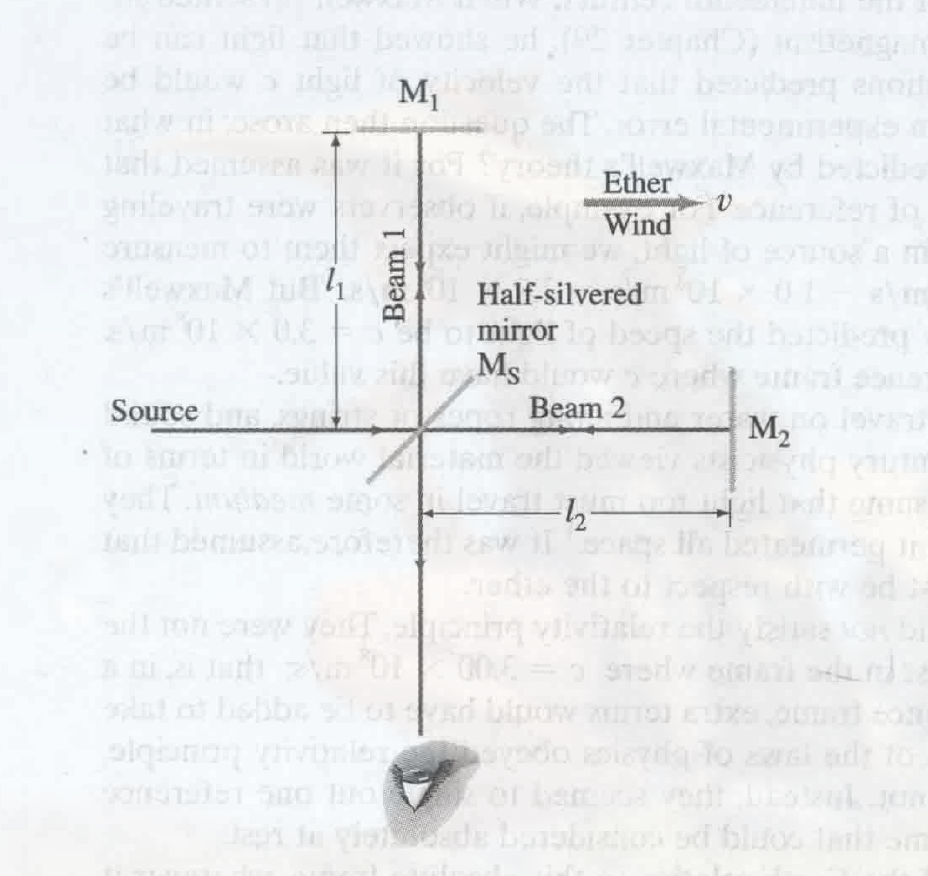
32.2 迈克耳逊-莫雷实验 The Michelson-Morley Experiment

就是这个实验:

32.3 狭义相对论的假设 Postulates of the Special Theory of Relativity

爱因斯坦的两个假设:

1. 在所有参考系中, 物理定理都有相同的形式 (而不是相同)
2. 光在无介质的空间传播, 光速不管是相对于观察者还是发射源, 速度都为 c (这里也就放弃了 ether 的假说, 实际上 ether 也从未被发现)

这两个假设是爱因斯坦相对论的基础.

加上 special (狭义) 是为了和爱因斯坦之后发布的 general theory of relativity 相区分.

Michelson-Morley 实验也和光速不变相吻合. (光速不变指的是光在真空中传播时, 在任何参考系中的速度不变, 而不是光在任何介质中都不变, 实际上, 水中的光速是空气中的光速的 1/3, 空气中的光速是真空中的光速的 1/4)

32.4 同时性 Simultaneity

狭义相对论中的同时性指, 事件发生的位置和时间是相对的，即两个事件在一个参照系中可以同时发生，但在另一个参照系中可能不同时发生。

见 另一篇文章.

这里利用一个思想实验来验证同时性是否存在.

32.5 时间膨胀和双生子悖论 Time Dilation and the Twin Paradox

速度越大, 时间越慢

例子如:

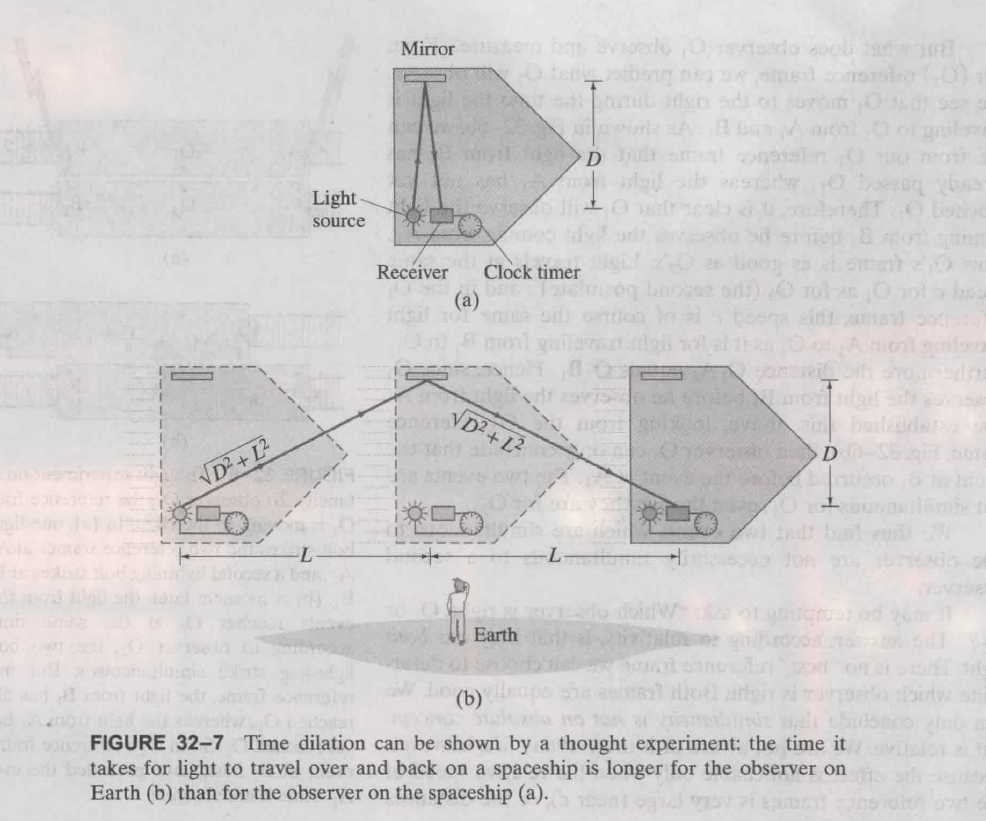
图 $(a)$ 为飞船, 以速度 $v$ 向右运动, 图 $(b)$ 有人站在地球上观察.

飞船上的人用光源向对面的镜子发射光束, 镜子与光源之间的距离为 $D$, 因此所用的时间为:

$$
\displaylines{\Delta t_0 = \frac{2D}{c}}
$$

对于地球上的人, 光束的飞行距离为:

$$
\displaylines{ 2 \sqrt{D^2 + L^2} \newline~ \newline
2L = v \Delta t \newline~ \newline
距离最终为: \newline~ \newline
\frac{2 \sqrt{D^2 + \frac{v^2(\Delta t)}{4}}}{\Delta t}}
$$

所花的时间为:

$$
\displaylines{\Delta t = \frac{\frac{2 \sqrt{D^2 + \frac{v^2(\Delta t)}{4}}}{\Delta t}}{c} \newline~ \newline
= \frac{2D}{c \sqrt{1- \frac{v^2}{c^2}}} \newline~ \newline
带入 \Delta t_0 = \frac{2D}{c} 得: \newline~ \newline
\Delta t = \frac{\Delta t_0}{\sqrt{1 - \frac{v^2}{c^2}}}}
$$
(这里 $\Delta t_0$ 可以看作速度快的物体的时间, 也就是速度快的物体在自己的参考系中测得的时间)

这里 $\sqrt{1- \frac{v^2}{c^2}} < 1$, 因此 $\Delta t > \Delta t_0$. 这就是 时间膨胀 (time dilation) 即速度快的物体时间慢.

双生子悖论 (twin paradox) 指:

32.6 长度收缩 Length Contraction

速度快的物体, 长度会变短

其推导过程利用了时间膨胀, 如:

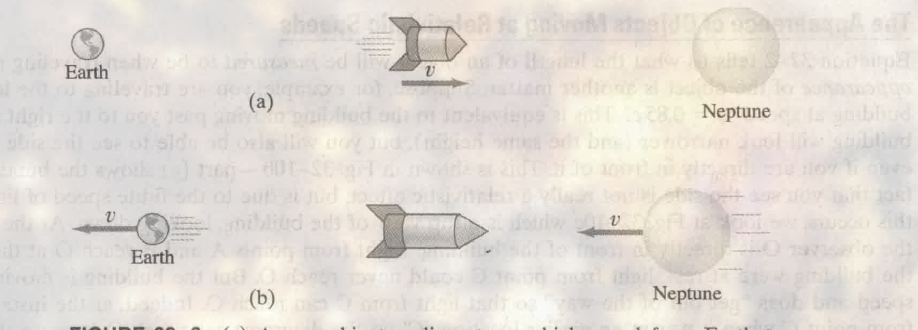
图 $(a)$, 地球上的观察者, 飞船以速度 $v$ 向 Neptune 靠近, 假设地球到 Neptune 的距离为 $L_0$, 那么:

$$
\displaylines{\Delta t = \frac{L_0}{v}}
$$

图 $(b)$, 飞船上的观察者, 此时飞船飞行的时间为:
$$
\displaylines{\Delta t_0 = \Delta t \sqrt{1- \frac{v^2}{c^2}} \newline~ \newline
此时飞行的总距离为: \newline~ \newline
L = v \Delta t_0 = v \Delta t \sqrt{1 - \frac{v^2}{c^2}} = L_0 \sqrt{1 - \frac{v^2}{c^2}}}
$$

从最后的式子:

$$
\displaylines{L =L_0 \sqrt{1 - \frac{v^2}{c^2}}}
$$

可以看出, 长度缩短.

32.8 伽利略和洛伦兹变换 Galilean and Lorentz Transformations

伽利略和洛伦兹变换 是关于不同参考系中位置和速度的变换.

这里有两个变换:

• 伽利略变换
• 洛伦兹变换

推导伽利略变换

对于:

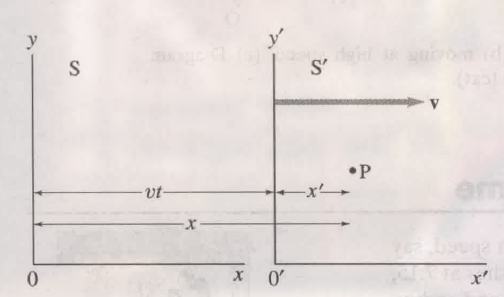
坐标系以速度 $v$ 向右移动. ( $t=0$ 的时候两个坐标系重叠)

有:

$$
\displaylines{x = x^\prime + v t^\prime \newline~ \newline
y = y^\prime \newline~ \newline
z = z^\prime \newline~ \newline
t = t^\prime}
$$

这里的 $x,y,z$ 是, 点 P, 关于原点 $O$ 的坐标.

这里的 $x^\prime,y^\prime,z^\prime$ 是, 点 P, 关于原点 $O^\prime$ 的坐标.

假设 P 点在 $S^\prime$ 参考系中的速度向量为 $u_x^\prime, u_y^\prime, u_z^\prime$, 有:

$$
\displaylines{u_x^\prime = \frac{dx^\prime}{dt^\prime} \newline~ \newline
u_y^\prime = \frac{dy^\prime}{dt^\prime} \newline~ \newline
u_z^\prime = \frac{dz^\prime}{dt^\prime}}
$$

假设在 S 参考系中的速度向量为 $u_x, u_y, u_z$, 有

$$
\displaylines{u_x = \frac{dx}{dt} = \frac{d(x^\prime + vt^\prime)}{dt^\prime} = u_x^\prime + v \newline~ \newline
u_y = u_y^\prime \newline~ \newline
u_z = u_z^\prime
}
$$
( 这里的 $u^\prime_x$ 是物体在自己参考系中的速度 )
这被称为 伽利略速度变换方程 (Galilean velocity transformation equations)

如果 $u_x$ 和 $u_x^\prime$ 在方程中位置对调, 即逆方程, $v$ 需要变为 $-v$.

伽利略变换只能用于速度远小于 c 时.

洛伦兹变换 (Lorentz transformation equations) 用于处理速度大的情况.

推导洛伦兹变换

假设坐标系变换是线性的, 有:

$$
\displaylines{x = \gamma (x^\prime + v t^\prime) \newline~ \newline
y = y^\prime \newline~ \newline
z = z^\prime }
$$

(伽利略变换就相当于 $\gamma = 1$)

由于 $x$ 和 $x^\prime$ 在方程中对调时, $v$ 需要改为 $-v$, 则有:

$$
\displaylines{x^\prime = \gamma(x - vt)}
$$

假设一个光脉冲从两个坐标系共同的原点发出 ( $t=0$ 时两个坐标系是重叠的), 则有:

$$
\displaylines{x = ct \newline~ \newline
x^\prime = ct^\prime \newline~ \newline
带入上式得: \newline~ \newline
ct = \gamma(ct^\prime + vt^\prime) = \gamma(c + v)t^\prime \newline~ \newline
ct^\prime = \gamma(ct - vt) = \gamma(c - v)t \newline~ \newline
}
$$
将 $t^\prime$ 替换为:

$$
\displaylines{t^\prime = \frac{\gamma(c + v)t}{c} \newline~ \newline
带入: ct = \gamma(c + v)t^\prime \newline~ \newline
得: ct = \gamma^2 (c^2 - v^2) \frac{t}{c} \newline~ \newline
化简得: \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}}
$$

利用:
$$
\displaylines{x = \gamma (x^\prime + v t^\prime) \newline~ \newline
x^\prime = \gamma(x - vt) \newline~ \newline
x^\prime = \gamma[\gamma(x^\prime + vt^\prime) - vt] \newline~ \newline
t = \gamma(t^\prime + \frac{v x^\prime}{c^2})}
$$

得到 $t$ 与 $t^\prime$ 的关系式.

最终的一组方程为:
$$
\displaylines{x = \gamma (x^\prime + v t^\prime) = \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}(x^\prime + v t^\prime) \newline~ \newline
y = y^\prime \newline~ \newline
z = z^\prime \newline~ \newline
t = \gamma(t^\prime + \frac{v x^\prime}{c^2}) = \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}(t^\prime + \frac{v x^\prime}{c^2}) }
$$

推导洛伦兹速度变换方程

利用: $u_x = \frac{dx}{dt}$ 等公式最终可得:

$$
\displaylines{u_x = \frac{u_x^\prime + v}{1 + \frac{vu_x^\prime}{c^2}} \newline~ \newline
u_y = \frac{u_y^\prime \sqrt{1-\frac{v^2}{c^2}}}{1 + \frac{vu_x^\prime}{c^2}} \newline~ \newline
u_z = \frac{u_z^\prime \sqrt{1-\frac{v^2}{c^2}}}{1 + \frac{vu_x^\prime}{c^2}} \newline~ \newline
}
$$
( 这里 $u_x^\prime$ 指物体在自己参考系中的速度)

32.9 相对论动量和质量

最终结论

$$
\displaylines
{
p = \frac{mv}{\sqrt{1-v^2/c^2}} = \gamma mv
}
$$

相对质量有:

$$
\displaylines
{
m_{rel} = \frac{m}{\sqrt{1-v^2/c^2}}
}
$$

具体分析

经典动量定义为 $p = mv$. 其是一个保守量 (即, 和路径无关).

分析时, 假设相对论中仍满足动量守恒定理

此时假设 $p = fmv$, $f$ 是 $v$ 的方程, $f(v)$. (因为在相对论的体系中, 动量的定义可能会变化)

实验目的是, 观察在动量守恒的条件下, $f(v)$ 的值.

假设两个相同的球, 且具有相同的速度, 可得知其具有相同的动量, 它们发生弹性碰撞,

思想实验为:

• 两个惯性坐标系, 沿着 x 轴以 v 的相对速度运动
• 在参考系 S 中, 球 A 沿着 y 轴向上以速度 $u$ 抛出
• 在参考系 $S^\prime$ 中, 球 B 沿着负 $y^\prime$ 轴向下以速度 $u$ 抛出
• 抛出的时间恰好能让两个球碰撞

如图:

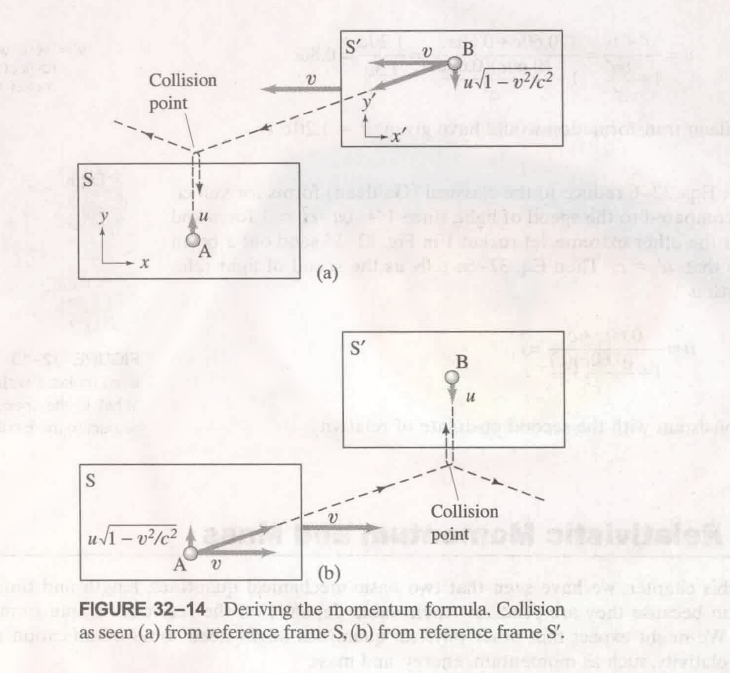
先从 S 参考系观察 A 球的运动, 可以这样分析, 时间为 $t$, 距离为 $l$, 碰撞前后速度大小都为 $u$.

再从 $S^\prime$ 参考系观察 A 球运动, 此时, 运动时间变为:

$$
\displaylines{t^\prime = \frac{t}{\sqrt{1 - v^2/c^2}} \newline~ \newline
距离仍然为: l \newline~ \newline
此时速度为: u^\prime = \frac{s}{t^\prime} \newline~ \newline
= \frac{l}{t} \sqrt{1 - v^2/c^2} \newline~ \newline
因此: u^\prime = u \sqrt{1 - v^2/c^2}}
$$
(记忆技巧, 你是站着不动的, 动的那个的速度需要乘 $\sqrt{1 - v^2/c^2}$)

这里从图 $(b)$ 也能得出 B 球的结果.

假设 $u \ll v$, 则球 A 的总动量可以写为 $f(v)mv$ (也就是说动量前的系数都可以写成 $f(v)$), 在参考系 S 中, 若对 y 轴应用动量守恒定理:

$$
\displaylines{f(u)mu - f(v)mu \sqrt{1-v^2/c^2} = -f(u)mu + f(v)mu \sqrt{1 - v^2/c^2} \newline~ \newline
f(v) = \frac{f(u)}{\sqrt{1-v^2/c^2}}}
$$

又假设 $u$ 非常小, 趋近于零, 此时就不再处于相对论领域, $f(u)mu$ 可以写成 $mu$, 因此 $f(u)=1$, 方程变为:

$$
\displaylines
{
f(v) = \frac{1}{\sqrt{1-v^2/c^2}}
}
$$

此时 $f(v)$ 的值就和 $\gamma$ 相同. 因此动量可以定义为:

$$
\displaylines
{
p = \frac{mv}{\sqrt{1-v^2/c^2}} = \gamma mv
}
$$

这里对动量的定义, 也可以理解为 质量的增加 , 因此以经典的写法, 可以写为:

$$
\displaylines
{
p = m_{rel} v
}
$$

这个 $m_{rel}$ 就叫做 相对质量 (relativistic mass), 有:

$$
\displaylines
{
m_{rel} = \frac{m}{\sqrt{1-v^2/c^2}}
}
$$
( $m$ 为静止时的质量, 其必须在一个它为静止的参考系中测量, $m_{rel}$ 是在一个它为运动的参考系中测量)

因此可以总结到, 速度变大的物体的质量也变大

在相对论中, 牛顿第二定理可以写为:

$$
\displaylines
{
F = \frac{dp}{dt} = \frac{d}{dt} ( \gamma mv ) = \frac{d}{dt} ( \frac{mv}{\sqrt{1-v^2/c^2}} )
}
$$

32.10 极限速度 The Ultimate Speed

狭义相对论的一个基本结论是: 物体的速度不能等于或超过光速.

32.11 能量和质量; $E = mc^2$

物体在相对论中的质量随速度增加而增加.

在一个物体上做功, 不仅会增加其速度, 还会增加其惯性. 正常情况下, 在一个物体上做功, 会增加其能量. 将这两个观点结合起来, 得出, 质量是能量的一种形式.

为了找到能量和质量之间的关系, 这里假设功-能定理在相对论中依然有效.

做功使粒子沿 x 轴运动, 将粒子的速度从 0 加速到 $v$ 所做的功为:

$$
\displaylines{W = \int_i^f Fdx = \int_i^f \frac{dp}{dt} dx = \int_i^f \frac{dp}{dt} v dt = \int_i^f v dp}
$$
(i 表示 initial ( $v=0$), f 表示 final ( $v=v$))

因为:

$$
\displaylines{d(pv) = p dv + v dp \newline~ \newline
v dp = d(pv) - p dv \newline~ \newline
W = \int_i^f d(pv) + \int_i^f pdv \newline~ \newline
\because \int_i^f d(pv) = pv \vert_i^f = (\gamma mv)v = \frac{mv^2}{\sqrt{1 - v^2/c^2}} \newline~ \newline
又 \because \frac{d}{dv} (\sqrt{1 - v^2 / c^2}) = -( v/c^2) / \sqrt{1- v^2 / c^2} \newline~ \newline
\therefore - \int_i^f pdv = - \int_0^v \frac{mv}{\sqrt{1 - v^2/c^2}}dv = mc^2 \sqrt{1 - v^2/c^2} \vert_0^v \newline~ \newline
= mc^2 \sqrt{1-v^2/c^2} - mc^2
}
$$

最终有:

$$
\displaylines
{
W = \frac{mc^2}{\sqrt{1-v^2/c^2} - mc^2}
}
$$

利用功-能定理, 做的功和最终的动能相同:

$$
\displaylines
{
K = \frac{mc^2}{\sqrt{1-v^2/c^2}} - mc^2 \newline~ \newline
= \gamma mc^2 - mc^2 = (\gamma-1)mc^2
}
$$

把质量视为一种能量, 爱因斯坦把 $mc^2$ 视为物体的 静止能量 (rest energy) , 因此总能量就是静止的加上动能的, 有:

$$
\displaylines
{
E = K + mc^2 \newline~ \newline
E = \gamma mc^2 = \frac{mc^2}{\sqrt{1-v^2/c^2}}
}
$$
这就称为物体的总能量.

同样有:

$$
\displaylines
{
\Delta E = (\Delta m)(c^2)
}
$$

文后还有一个公式:

$$
\displaylines
{
需要利用 \newline~ \newline
E = \gamma m c^2 \ \ 和 p = \gamma mv \newline~ \newline
E = \gamma m c^2 = \frac{m c^2}{ \sqrt{1-v^2/c^2} } \newline~ \newline
E^2 = \frac{m^2 c^4}{1 - v^2/c^2} \newline~ \newline
= \frac{m^2 c^2 (v^2 - v^2 + c^2)}{1 - v^2/c^2} \newline~ \newline
= \frac{m^2 c^4 (v^2/c^2 - v^2/c^2 + 1)}{1 - v^2/c^2} \newline~ \newline
= \frac{m^2 c^4 (1 - v^2/c^2) + m^2 c^2 v^2}{1 - v^2/c^2} \newline~ \newline
= \frac{m^2 c^4 (1 - v^2/c^2) + m^2 v^2 c^2}{1 - v^2/c^2} \newline~ \newline
(注意这里的 \frac{m^2 v^2}{1 - v^2/c^2} = p^2) \newline~ \newline
= p^2 c^2 + \frac{m^2 c^4 (1 - v^2/c^2)}{1 - v^2/c^2} \newline~ \newline
= p^2c^2 + m^2 c^4
}
$$

Chapter 33 早期量子理论和原子模型 Early Quantum Theory And Modles of The Atom

大部分原子的信息, 来自, 由该原子构成的纯净的材料发出的光中. (也就是分析光谱)

33.1 普朗克的量子假设 Planck’s Quantum Hypothesis

热体发出光的光谱在 19 世纪无法得到解释.

在热力学中, 所有物体发出的射线的总强度应该和开氏温度的 4 次方成正比 ($T^4$).

黑体和黑体辐射. 黑体指, 吸收所有照向它的辐射的东西. 其在高温下会发出辐射, 其发射的辐射强度仅仅依赖于其温度，而与其它物理特性无关, 这个辐射就叫做黑体辐射.

在不同温度下黑体发出的辐射不同, 如 6000-K 和 3000-K :

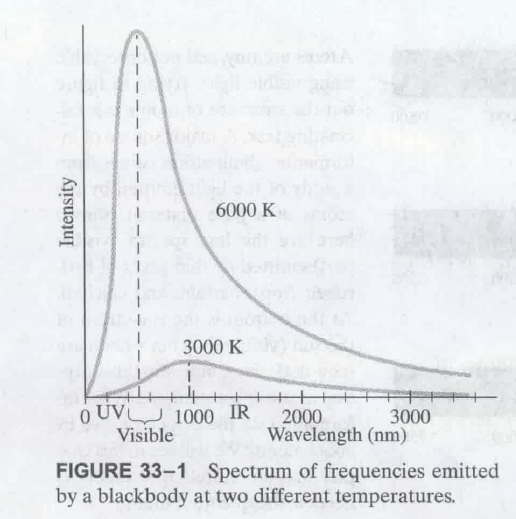
(这里曲线的含义为, 拿 6000-K 为例, 横轴表示辐射的范围, 纵轴表示强度, 此时发出的射线中, 频率为可见光的这一部分强度最大, 这也是为什么我们能观察到)

实验表明, 频谱的最高点所在的频率 $\lambda_p$ 和开尔文温度的关系为:
$$
\displaylines{\lambda_p T = 2.90 \times 10^{-3} m \cdot K}
$$

这个公式称为 Wien’s law.

公式的应用, 也就是可以求一个发光体的颜色

星星表面温度为 $32500K$, 求这个星星的颜色:

$$
\displaylines{ \lambda_p T = 2.90 \times 10^{-3} \newline~ \newline
\lambda_p = \frac{2.90 \times 10^{-3}}{ 3.25 \times 10^{4}} \newline~ \newline
= 89.2nm}
$$

问题出在了 解释黑体辐射 上. 两个科学家 (W.Wien 和 Lord Rayleigh) 的理论出现不同, 且都和实验有部分偏差.

对比图:

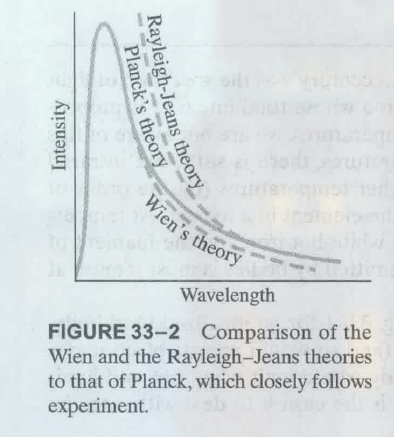
Max Planck (普朗克) 的一个公式完美的符合实验数据:

$$
\displaylines{I(\lambda, T) = \frac{2 \pi h c^2 \lambda^{-5}}{e^{hc/\lambda k T} - 1}}
$$

这里, $I(\lambda, T)$ 是辐射的强度 (关于波长和温度的函数), $k$ 代表 Boltzman’s constant (玻尔兹曼常量), $c$ 代表光速, $h$ 是一个新的常量, 现在叫 Planck’s constant (普朗克常量). 为了让公式符合实验, 普朗克添加了这个常量并估计其值. 现在这个精确的值为:

$$
\displaylines{h = 6.626 \times 10^{-34} J \cdot s}
$$

后来, 普朗克假设, 能量不是连续的, 而是由离散的量组成, 其值和振荡频率有关:

$$
\displaylines{E_{min} = h f}
$$

且能量只能为其整数倍:

$$
\displaylines{E = nh f, \ n = 1,\ 2,\ 3,…}
$$

这个想法就被叫做, 普朗克量子假设 , 其认为能量不是连续的, 而是可量化的, 即存在离散量. 最小的能量 ($hf$) 就被叫做 quantum of energy (能量量子)

33.2 光的光子理论和光电效应 Photon Theory of Light and the Photoelectric Effect

爱因斯坦假设 光是以极小的微粒传递, 即 photons (光子, 其是一个能量单位, 一个光子为 $E = hf$)

光电效应 是一个现象, 即光在照射金属板时, 电子会从金属板发射. (光子与金属板上的电子碰撞, 使其携带能量)

photocell (光电元件), 指一个金属版和一个电极放置在一个疏散的玻璃管中构成的器件, 如:

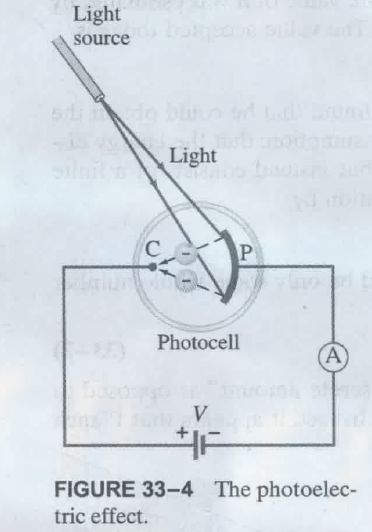
这里, 光电效应是否发生是通过 电流表的示数 .

stopping voltage (截止电压, $V_0$), 即, 将上述电路中的电源 (此时为可变化的电源, 通过调整这个电源来改变电源产生电场的大小, 毕竟此时光照强度不会改变) 两极反转, 此时光电元件中有一个电源引发的电场, 而当光电元件本身引发的电场和其抵消时, 此时的电压即截止电压, 可求得电子的最大动能为:
$$
\displaylines{K_{max} = e V_0}
$$
(这里的理解为, 电子要从金属板到达电极, 要受到电场力的作用 $F = qE = q \frac{V}{d}$, 此时的功为: $Fd = qV = e V_0$, 电压 $V_0$ 本就代表电子运动一段距离所消耗的能量)

光的波动中, 最重要的性质是:

• 强度
• 频率 (或者说波长, 因为 $\lambda = \frac{c}{f}$)

下面分别讲述两个理论的预测, 波动理论和粒子理论的预测结果差别很大. (最后表面粒子理论符合实验预期, 因此这里的波动理论预测被注释掉了, 可以在源码中查看)

光的粒子理论预测:

在单色光束中, 增加光强意味着增加光子的数量, 而单个光子的能量不变 (毕竟频率没变, $E = hf$). 光子碰撞电子后, 将传递全部的能量.

让电子脱离金属的控制需要的功 $W_0$ 称为 work function (功函数).

如果 $W_0 > hf$ (即需要的能量大于传递的能量), 则电子无法脱离.

如果电子从金属板到达电极所消耗的动能为 $K$, 那么光子的能量为:

$$
\displaylines{hf = K + W}
$$
(也就是, 脱离金属表面的能量和到达电极的能量之和)

当需要的动能最大时, 有:

$$
\displaylines{hf = K_{max} + W_0}
$$

其预测内容为:

1. 光强增大, 意味着更多光子射出, 更多的电子会发出, 但电子的最大动能不变 (毕竟光子的频率不变, 能量也就不变, 电子得到的能量也不会变)
2. 光的频率增大, 电子的最大动能变大
3. 若光的频率低于截止频率 $f_0$, (有 $hf_0 = W_0$), 不会有电子发出, 不管光强有多大

光的频率和最大动能的关系图:

光电效应的应用 Applications of the Photoelectric Effect

自动开门, 烟雾检测.

真空管的光电元件被光电二极管 (photodiode) 取代.

33.3 光子和康普顿效应 Photons and the Compton Effect

A.H.Compton 发现, 用一些材料散射短波长光 (如 X 射线) 时, 散射出的光的波长大于入射光 (即频率小于入射光, 也就是能量减小). 他利用光子理论的基础解释为, 入射光的光子和材料的电子发生了碰撞.

示意图为:

利用能量守恒定理和动量定理发现吻合实验结果.

光子的速度 为光速. 利用相对论公式可以计算其质量, 能量和动量.

计算质量

质量假设为 0.

计算能量

若波长为 $\lambda$, 则:

$$
\displaylines{E = hf \newline~ \newline
\because f = \frac{c}{\lambda} \newline~ \newline
\therefore E = \frac{hc}{\lambda}}
$$

计算动量

根据 $E^2 = p^2 c^2 + m^2 c^4$, 若质量为零 $m = 0$, 那么:

$$
\displaylines{p = \frac{E}{c} \newline~ \newline
\because E = hf,\ c = \frac{\lambda}{f} \newline~ \newline
\therefore p = \frac{hf}{c} = \frac{h}{\lambda}}
$$

以 $\phi$ 角度散射出的光的波长假设为 $\lambda^\prime$, 其能量和动量为

$$
\displaylines{E^\prime = \frac{hc}{\lambda^\prime}\ and\ p^\prime = \frac{h}{\lambda^\prime}}
$$

被碰撞的电子的动能和动量

假设电子在碰撞之前为静止, 根据相对论中的公式得其动能为:

$$
\displaylines{K = \frac{mc^2}{\sqrt{1- \frac{v^2}{c^2}}} - mc^2 \newline~ \newline
K_e = ( \frac{1}{\sqrt{1 - \frac{v^2}{c^2}} - 1}) m_e c^2 }
$$

这里的 $m_e$ 为电子静止时的质量, $v$ 是其速度.

电子的动量为:
$$
\displaylines{ p_e = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}m_e v}
$$

对碰撞过程应用能量守恒定理 (一个光子碰撞一个静止电子, 得到能量减小的光子和获得动能的电子):

$$
\displaylines{ \frac{hc}{\lambda} = \frac{hc}{\lambda^\prime} + ( \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}) m_e c^2 }
$$

将过程分为 x 轴和 y 轴分别分析:

$$
\displaylines{x轴:\ \frac{hc}{\lambda} = \frac{hc}{\lambda^\prime} \cos \phi + \frac{m_e v \cos \theta}{\sqrt{1 - \frac{v^2}{c^2}}} \newline~ \newline
y轴:\ 0 = \frac{hc}{\lambda^\prime} \sin \phi - \frac{m_e v \sin \theta}{\sqrt{1 - \frac{v^2}{c^2}}}}
$$

联立上述公式可以消除 $v$ 和 $\theta$:
$$
\displaylines{\lambda^\prime = \lambda + \frac{h}{m_e c} (1 - \cos \phi) \newline~ \newline
(证明过程简略) }
$$

此时可以得知, 当 $\theta = 0$ 时, 波长没有改变.

当某个角度, 至 $\lambda^\prime > \lambda$ 时:

$$
\displaylines{\Delta \lambda =\lambda^\prime - \lambda = \frac{h}{m_e c} (1 - \cos \phi)}
$$

这个现象叫做 Compton shift (康普顿位移), 而 $\frac{h}{m_e c}$ 的单位是长度, 也被叫做 电子的 Compton wavalength $\lambda_C$(电子的康普顿波长) :

$$
\displaylines{\lambda_C = \frac{h}{m_e c} = 2.43 \times 10^{-3}nm = 2.43pm}
$$
(电子的质量为 $9.11 \times 10^{-31}$)

光的波动理论没有预测出 wavelength shift, 而这里的康普顿效应则是光的光子理论的实验验证.

33-4 Photon Interactions; Pair Production

当光子穿过物质时, 可能有四种情况发生:

1. 和康普顿效应预测相同, 碰撞后, 散射出电子, 光子损失能量, 但光子速度不变, 只是频率减小
2. 和光电效应预测相同, 碰撞后, 电子被撞出原子, 光子消失
3. 光子的能量如果不足以将电子撞出, 则使电子从低能级跃迁到高能级, 光子消失
4. Pair production, 光子创造物质, 产生电子和正电子, 同时光子消失, 如图;

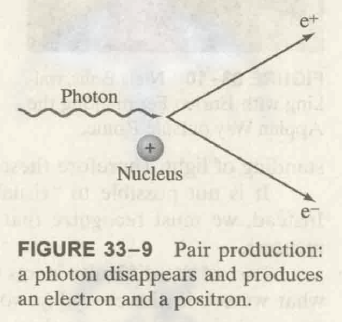
Pair production 是一个从纯净能量产生静止质量的例子, 且其符合爱因斯坦的质能方程 $E = m c^2$. pair production 的逆过程为, 当电子碰撞正电子, 两个粒子湮灭 (包括能量和质量), 形成光子的电磁能. (正因如此, 正电荷在自然界中无法长时间存在)

33-5 波粒二象性; 互补性原则 Wave-Particle Duality; the Principle of Complementarity

光电效应, 康普顿效应和其他实验是光的粒子理论的实验基础.

Young 和其他人在干涉和衍射方面的实验是 光的波动理论 的实验基础.

最终结论为, 光具有波粒二象性 .

Niels Bohr 的互补性原则. 其表明, 如果要真正理解光, 需要将波动理论和光子理论互补. (书中并没有直接的公式定理之类的, 似乎是一个声明)

我们不能直接 see directly whether light is a wave or particle.

33.6 物质的波动性 Wave Nature of Matter

Louis de Brogile (德布罗意) 扩展了波粒二象性的概念. 他非常欣赏自然界的对称. 他认为光 有时表现得像波, 有时表现得像粒子 . 因此, 自然界中的一些粒子, 如电子, 可能也有波的性质.

德布罗意认为 物质粒子的波长和动量有关 , 如：

$$
\displaylines{p = \frac{h}{\lambda} \newline~ \newline
\lambda = \frac{h}{p}}
$$

这个波长就叫做粒子的 de Broglie wavalength (德布罗意波).

普通物质的德布罗意波长非常小, 难以测量和检测出, 如:

例子, 一个 $0.20 kg$ 的球以 $15m/s$ 的速度滚动, 其德布罗意波为

$$
\displaylines{\lambda = \frac{h}{p} = \frac{h}{m v} = \frac{(6.6 \times 10^{-34} J \cdot s)}{(0.20kg)(25m/s)} = 2.2 \times 10^{-34}m}
$$

且波的性质, 如干涉和衍射需要当物体的尺寸不再远大于波长时才会明显显现.

但小微粒由于质量在分母, 往往会得到相对比较大的波长, 如:

例子, 求电子的波长, 其在电势差为 $100V$ 的电场中被加速

$$
\displaylines{\because \frac{1}{2} m v^2 = e V \newline~ \newline
v = \sqrt{ \frac{2e V}{m}} = \sqrt{ \frac{ (2)(1.6 \times 10^{-19}C) (1000V)}{(9.1 \times 10^{-31} kg)}} = 5.9 \times 10^6 m/s \newline~ \newline
\lambda = \frac{h}{mv} = \frac{(6.6 \times 10^{-34}J \cdot s)}{(9.1 \times 10^{-31} kg) (5.9 \times 10^6 m/s)} = 1.2 \times 10^{-10}m}
$$

这个大小就可以被侦测到.

必须认识到, 我们不能直接看到 wave-paritcle 的图像, 就像没有人直接看到电子长什么样. 我们必须借助实验来建立模型.

我们不应该直接认为电子是一个波或者一个粒子, 相反, 我们应该认为, 电子是一个测量的性质的集合.

33.7 电子显微镜 Electron Microscopes

电子有波的性质, 促进了电子显微镜的发展.

具体见书.

33.8 早期的原子模型 Early Models of the Atom

最开始的 糕点模型 plums in pudding

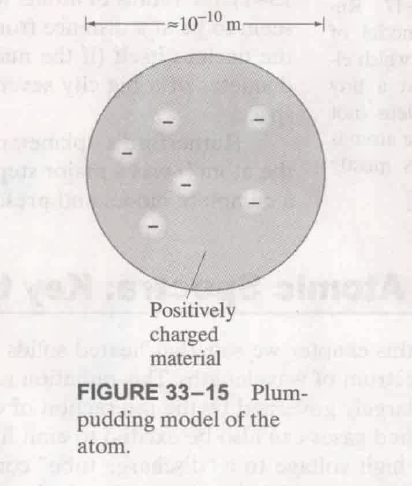
该模型表示, 原子是实心的带正电的球体, 带负电的电子镶嵌在其中.

Rutherford’s planetary model, 卢瑟福的模型

带负电的电子围绕一个带正电的极小的原子核, 原子中的大部分为空的空间. 卢瑟福的实验预测, 原子核的半径为 $10^{-15} \sim 10^{-14}m$, 而从爱因斯坦的分析, 原子的半径为大约 $10^{-10}m$.

这个模型是从$\alpha$ 粒子散射实验 中预测出的.

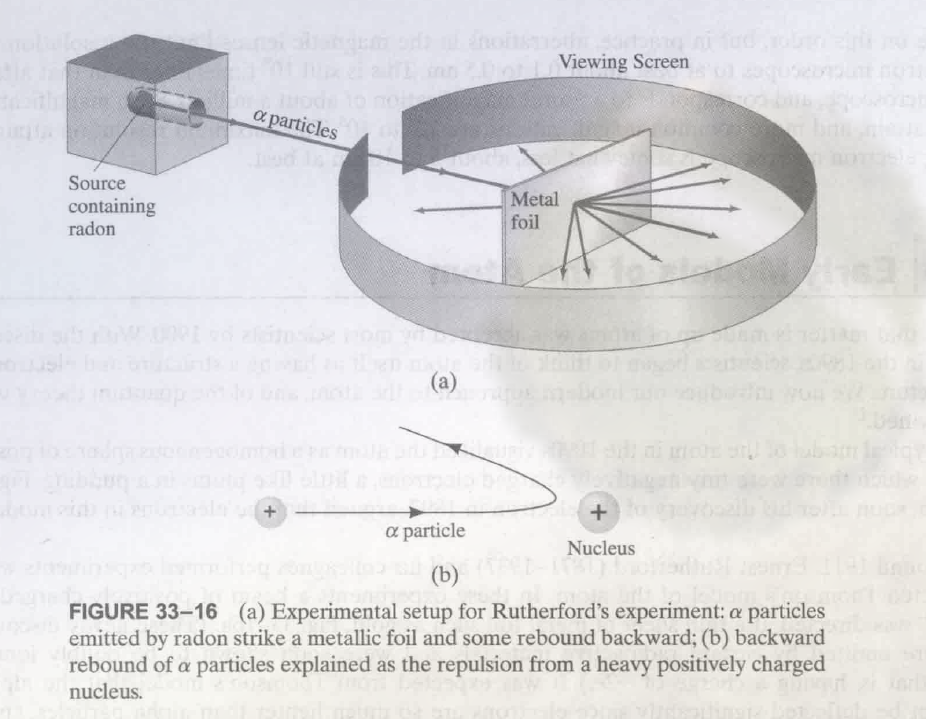
实验现象为, 大部分 $\alpha$ 粒子直接穿过, 小部分以大角度变化反弹.

33.9 原子光谱: 原子结构的关键 Atomic Spectra: Key to the Structure of the Atom

热的物体发出辐射, 原因认为是原子和分子的振动.

让稀有气体激发并发出光线的方法有:

• 加高热, 将稀有气体加热到一定温度，会使气体原子或分子中的电子被激发到高能级，当电子返回到低能级时也会发出光线
• 放在低压的管子中, 并加上高压, 电场会激发稀有气体中的电子，使其跃升到更高的能级。当电子返回原来的能级时，会放出能量以光子的形式发射出光线

这些辐射的光谱是不连续的, 因为激发的气体只会辐射几种波长.

当用光谱仪, 分光镜分析这些光时, 也发现了线谱 (line spectrum) 而不是连续的光谱. 如:

(这里的白线黑线应该就是线谱)

发射光谱 (emission spectrum) 是材料的特性, 能够用于区分气体.

发射光谱是指物质在激发条件下所发射的光的谱线。当一个物质受到能量的激发，例如通过加热或电离等方式，它的原子或分子会跃迁到高能级状态，当它们从高能级状态返回到低能级状态时，会发出电磁辐射，这些辐射就包括可见光。这些发出的光在经过分光仪分散后，就会形成一组亮的谱线，这些谱线的颜色、强度、位置等都可以提供关于物质本身的信息，因此可以用于物质的分析和识别。

吸收光谱的定义

吸收光谱是指物质在吸收电磁辐射时，产生的一组特定的波长或频率上的吸收峰的谱线。当物质吸收特定波长的光时，它的分子或原子的电子跃迁到更高的能级，从而吸收能量，这些吸收带的位置、强度和形状与物质的化学成分和结构相关。因此，通过对物质吸收光谱的研究，可以确定物质的成分和结构，以及浓度等信息。

大部分原子的光谱图没有明显的规律性, 而氢原子的光谱图有, 其从第三条开始满足公式:

$$
\displaylines{ \frac{1}{\lambda} = R ( \frac{1}{2^2} - \frac{1}{n^2}),\ n=3,4,…}
$$
( $R$ 为 Rydberg constant 雷德博格常量, 值为 $10.074 \times 10^7 m^{-1}$)

这里, $n$ 从 3 开始, 这个公式被称为 Balmer series (巴尔默公式). 当 $\lambda = 365nm$ 时, 认为 $n = \infty$.

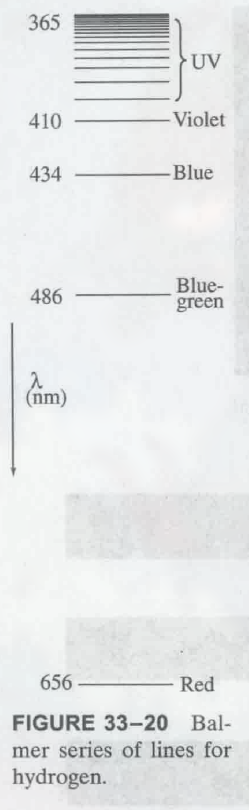
Lyman series

$$
\displaylines{ \frac{1}{\lambda} = R ( \frac{1}{1^2} - \frac{1}{n^2}),\ n=2,3… \newline~ \newline
91nm \le \lambda \le 122nm}
$$

Paschen series

$$
\displaylines{ \frac{1}{\lambda} = R ( \frac{1}{3^2} - \frac{1}{n^2}),\ n=4,5… \newline~ \newline
820nm \le \lambda \le 1875nm}
$$

卢瑟福的模型不能解释为什么粒子会释放 line spectra. 两个难题:

1. 其预测粒子会释放连续频率的波, 而实验为 line spectra 即不连续
2. 其预测原子是不稳定的, 但实际上是稳定的

33.10 波尔模型 The Bohr Model

从 Planck 和 Einstein 的实验, 能量的改变是不连续的. Bohr 表明, 一个原子中的电子不能连续的失去能量, but do so in quantum “jumps”. (和量子只能是 $hf$ 的倍数一个道理)

Bohr 假设, 电子在原子核周围的轨道上运动, 电子在每一个轨道上会有确切的能量, 且在同一个轨道上运动不会释放能量. 这些轨道被称为 静止状态 stationary states, 发射光线时, 电子会从 stationary state 跳到低能量的 stationary state. (也就是高能级到低能级) 每一跳会释放一个光子的能量, 即:

$$
\displaylines{hf = E_u - E_l \newline~ \newline
(u 指 upper, l 指 lower)}
$$

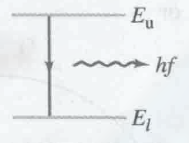
Bohr’s quantum condition

$$
\displaylines{ L = I \omega \newline~ \newline
I = m r^2,\ \ \omega = \frac{v}{r} \newline~ \newline
L = (m r^2)( \frac{v}{r} )= m v r_n = n \frac{h}{2 \pi},\ n=1,2,3…}
$$
这里, $L$ 指角动量, $r_n$ 指第 n 个轨道的半径, $v$ 指速度. 这个 n 同时被称为轨道的量子数 (quantum number)

推导轨道半径

示意图为:

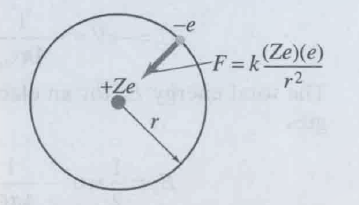
电子在半径为 $r_n$ 的轨道上运动时会有角加速度 $\frac{v^2}{r_n}$ (由原子和正电荷和电子产生的作用力引起)

$$
\displaylines{结合库仑定理 \newline~ \newline
电子受到的力: F = \frac{1}{4 \pi \epsilon_0} \frac{(Ze)(e)}{r^2} \newline~ \newline
(Z 是正电荷数量) \newline~ \newline
由牛顿第二定律: \newline~ \newline
F = ma \newline~ \newline
以及: \newline~ \newline
a = \frac{v^2}{r_n} \newline~ \newline
得: \frac{1}{4 \pi \epsilon_0} \frac{Z e^2}{r_n^2} = \frac{m v^2}{r_n} \newline~ \newline
解出 r_n 为: \newline~ \newline
r_n = \frac{Ze^2}{4 \pi \epsilon_0 m v^2} \newline~ \newline
\because v = \frac{nh}{2 \pi m r_n} (上面的 Bohr’s quantum condition) \newline~ \newline
\therefore r_n = \frac{Ze^2 4 \pi^2 m r_n^2}{4 \pi \epsilon_0 n^2 h^2} \newline~ \newline
抵消两边的 r_n 并化简: \newline~ \newline
r_n = \frac{n^2 h^2 \epsilon_0}{\pi m Z e^2} = \frac{n^2}{Z} r_1 \newline~ \newline
r_1 = \frac{h^2 \epsilon_0}{\pi m e^2} \newline~ \newline
(r_1 指 n = 1, Z = 1 时的值)
}
$$

氢原子轨道的最小轨道的半径 $r_1 = 0.529 \times 10^{-10}$ 被称为 Bohr radius.

轨道上的能量计算

总能量为动能加上势能.

$$
\displaylines{V = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r} = \frac{1}{4 \pi \epsilon_0} \frac{Ze}{r} \newline~ \newline
U = -eV = - \frac{1}{4 \pi \epsilon_0} \frac{Ze^2}{r}}
$$

第 n 个轨道上的能量为:
$$
\displaylines{E_n = \frac{1}{2}m v^2 - - \frac{1}{4 \pi \epsilon_0} \frac{Ze^2}{r}}
$$

带入:
$$
\displaylines{v = \frac{nh}{2 \pi m r_n} \newline~ \newline
r_n = \frac{n^2 h^2 \epsilon_0}{\pi m Z e^2}}
$$

得:
$$
\displaylines{E_n = -( \frac{Z^2 e^4 m}{8 \epsilon_0^2 h^2}) ( \frac{1}{n^2})\ n=1,2,3… \newline~ \newline
E_n = \frac{Z^2}{n^2}E_1\ n=1,2,3… \newline~ \newline
(E_1 为 n=1, Z=1 时) \newline~ \newline
E_1 = - \frac{m e^4}{8 \epsilon_0^2 h^2} = -2.17 \times 10^{-18}J = -13.6eV}
$$

最低的能级 (energy level or energy state) 的能量为 E_1, 被称作 基态 (ground state) . 其余高能级都被称作 激发态 (excited states)
(内层是低能级, 外层是高能级, 比较激发是往外激发, 激发到最后是脱离)

注意所有的能级的能量都是低于 0. (这样理解, 一个电子从外界到原子核所需要的能量, 越到内部, 即越到低能级所需要的能量越多, 负得也就越多, 原子外就相当于 0)

将电子从基态到离开原子所需要的能量称为 结合能或电离能 (binding energy or ionization energy).

氢原子的电离能大概为 $13.6eV$.

处于不同能级的电子具有不同的频率?

$$
\displaylines{f = \frac{c}{\lambda} \newline~ \newline
hf = h \frac{c}{\lambda} \newline~ \newline
\because hf = E_n - E_{n^\prime} \newline~ \newline
(hf = E_u - E_l 这个公式) \newline~ \newline
\therefore \frac{1}{\lambda} = \frac{1}{hc} (E_n - E_{n^\prime}) \newline~ \newline
\because E_n = -( \frac{Z^2 e^4 m}{8 \epsilon_0^2 h^2}) ( \frac{1}{n^2})\ n=1,2,3… \newline~ \newline
\therefore \frac{1}{\lambda} = \frac{Z^2 e^4 m}{8 \epsilon_0^2 h^3 c}( \frac{1}{(n^\prime)^2} - \frac{1}{(n)^2})
}
$$

这个公式和 Balmer formula 有相同的形式.

当 $Z=1$ 时, $\frac{Z^2 e^4 m}{8 \epsilon_0^2 h^3 c}$ 的值和 Rydberg constant 值相同, $R = 1.0974 \times 10^7 m^{-1}$

Bohr’s theory 的成功之处在于 其解释了为什么原子会发出 line spectra, 以及准确预测出了发射光线的波长.

Bohr theory 同时 解释了吸收光谱 : 特定波长的光子撞击电子后使其从低能级到了高能级 (也就是吸收了能量, 也就是吸收光谱中特定频率处出现暗线的原因)

其也解释了原子的稳定性: 处于基态的电子不会因到达更低的能级而释放能量 (毕竟已经为最低了)

但是 Bohr theory 只解释了氢原子, 而没有解释其他原子.

Bohr theory 没有解释电子是怎样从一个能级到达另一个能级.

The Bohr model is only a model, not reality.

现代的电子 are better thought of as forming “clouds”. (电子云)

对于氢原子有:

$$
\displaylines
{
E = - \frac{13.6eV}{n^2}
}
$$

对于其他原子有:

$$
\displaylines
{
E = - Z^2 \frac{13.6eV}{n^2}
}
$$

33.11 德布罗意对原子的假设

在 Bohr 的理论中, 电子是做圆周运动, de Broglie 由此假设 electron wave 是 circulaar standing wave 如:

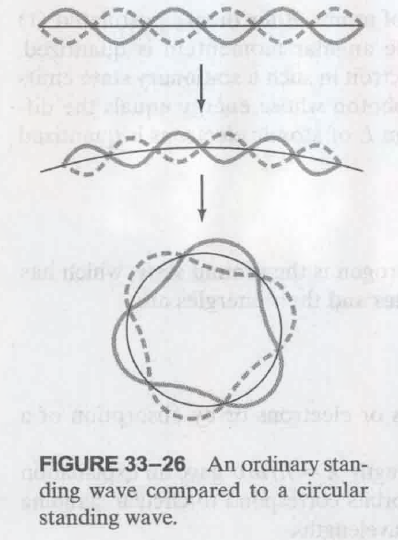
(这样波才不会因相消干涉而消失)

此时波长圆形轨道的周长:

$$
\displaylines{2 \pi r_n = n \lambda \ \ n = 1,2,3,… \newline~ \newline
(Bohr theory 中的轨道半径为 r_n) \newline~ \newline
结合: \lambda = \frac{h}{mv} \newline~ \newline
2 \pi r_n = n \frac{h}{mv} \newline~ \newline
mvr_n = \frac{nh}{2 \pi}}
$$

这也同时为 Bohr’s quantum condition.

很多东西 Bohr 的理论都无法解释, 而这些在 quantum mechanics 中得到了解决.

Bohr theory 的缺陷:

Chapter 34 量子力学 Quantum Mechanics

34.1 量子力学 – 一个新理论 Quantum Mechanics – A New Theory

量子力学 将波粒二象性统一到了一个理论中.

量子力学主要用于处理微观世界的粒子和光.

34.2 波动方程及其含义; 双缝实验 The Wave Function and Its Interpretation; the Double-Slit Experiment

波的重要性质有:

• 波长
• 频率
• 振幅

波动方程的符号为 $\psi$

薛定谔波动方程 (Schrodinger wave equation) 是描述非相对论物质粒子的基本方程.

薛定谔波动方程（Schrodinger Equation）是描述量子力学中非相对论性粒子的运动规律的基本方程。它由奥地利物理学家艾尔温·薛定谔于1925年提出，是量子力学的核心之一。

薛定谔波动方程描述了微观粒子（如电子、原子等）的波函数随时间和空间的演化。波函数是用于描述微观粒子状态的一种数学量，其绝对值的平方表示了粒子在某个位置出现的概率密度。薛定谔波动方程中的解是波函数，通过它可以计算得到粒子在不同时间和空间位置的概率分布。

对于一个粒子来说, 波动方程 $\psi$ 意味着其运动具有波粒二象性.

波粒二象性表明，微观粒子具有概率波函数（或简称波函数），其绝对值的平方表示了粒子出现在不同位置的概率分布.

在量子力学中，粒子的波函数满足薛定谔波动方程，这个方程描述了波函数随时间和空间的演化规律。通过求解薛定谔波动方程，可以得到粒子的波函数和能量本征值，从而得到粒子的运动和性质.

光线的能量密度正比于单位体积中光子的数量 n (同样正比于 $E^2$, E 为电场强度):

$$
\displaylines{n \propto E^2}
$$

这里需要理解, $E^2$ 在这里的作用就是表明在一个单位体积中光子出现的概率.

如果 $dV$ 表示无穷小的体积, $E^2 dV$ 就正比于在体积 $dV$ 中发现光子的概率.

如果 $\psi$ 描述很多电子, 那么 $\left\vert \psi \right\vert^2 dV$ 与期待出现在 $dV$ 中的电子的个数成正比.

如果 $\psi$ 描述一个电子, 那么$\left\vert \psi \right\vert^2$ 的解释为: $\left\vert \psi \right\vert^2 dV$ 表示在给定时间和空间下, 体积 $dV$ 中找到电子的概率.

因此, $\left\vert \psi \right\vert^2$ 被视为概率密度或概率分布.

将光线改为电子的双缝干涉实验, 用荧光屏反应电子的撞击 (在电子碰撞后会发光)

发射的电子流, 一次发射一个. 每次记录一个快照, 将快照叠加在一起, 结果如:

不能预测电子会撞击那里, 可以预测概率, 其与 $\left\vert \psi \right\vert^2$ 成正比.

就好像电子同时穿过光栅并和自己发生了干涉. 这时需要把电子视为波, 这样它就可以同时穿过两个光栅.

主要观点:

• 如果将电子视为波, $\psi$ 代表波的振幅
• 如果将电子视为粒子, 则 $\psi$ 代表概率

$\left\vert \psi \right\vert^2$ 同样代表在给定位置, 单位体积中发现电子的概率.

34.3 海森堡测不准原理 The Heisenberg Uncertainty Principle

不管测量工具有多精确, 都会有误差. 但是根据量子力学, 精确的测量都有一个限制. 其并不是来自器材. 取决于两个因素:

• 波粒二象性
• 被观察物体和观察器材不可避免的接触

在没有任何干扰的情况下测量一个物体是不可能的. 比如:

在光照下观察一个乒乓球, 为了能看到球, 至少一个光子会从乒乓球上散射, 反射的光子会进入你的眼睛或其他器材.

光子若落在电子上, 就会极大改变其运动.

观察物体的精确度, 最高为所用辐射的波长, 波长越小, 精确度越高, 但这意味着波的动量越大 ( $p = \frac{h}{\lambda}$), 也就是说物体受到的撞击就更强烈, 但使用波长长的波, 精确度又会下降.

因此, 观察物体的行为在电子的位置和动量上创造出了重要的误差, 这就是 测不准原理的本质, 且由 Heisenberg 首次阐述.

使用波长为 $\lambda$ 的波进行测量的最大误差为波长本身, 即:

$$
\displaylines{\Delta x \approx \lambda}
$$

假设用一个光子就能观察物体, 光子的动量为 $p = \frac{h}{\lambda}$, 且碰撞时传递全部动量, 则:

$$
\displaylines{\Delta p \approx \frac{h}{\lambda}}
$$

因此有:
$$
\displaylines{(\Delta x) (\Delta p) \approx h}
$$

由于误差可能更大 (更多的光子), 因此, 经过 Heisenberg 的计算, 最佳的为:
$$
\displaylines{(\Delta x) (\Delta p_x) \ge \frac{h}{2 \pi}}
$$
( $\Delta p_x$ 是x轴方向上的误差)

这个表达式也是 海森堡测不准原理的数学表达, 或者叫不确定原理.

其说明不能同时精确的测量物体的位置和动量. 如果要精确测量位置, $\Delta x$ 会很小, 但是 $\Delta p_x$ 会变得很大, 反之. (在动量改变后物体的下一个位置就未知了)

(这里的解题一般为, 已知一个量的误差, 求另一个量的误差, 这里的 $\Delta x$ 和 $\Delta p$ 表示的都是误差的量)

海森堡测不准原理关于时间和能量的形式:

用于测量物体的光子需要一段时间才能抵达物体, 而这段时间产生的误差就是之前的 $\Delta x$, 有 $\Delta t \approx \Delta x / c \approx \lambda / c$, 因此:

$$
\displaylines{\Delta t \approx \frac{\lambda}{c}}
$$

光子将全部能量传递给物体:

$$
\displaylines{E = hf = h \frac{c}{\lambda}}
$$

因此有:

$$
\displaylines{(\Delta E) (\Delta t) \approx h}
$$

最终关系式, 经海森堡仔细计算为:
$$
\displaylines{(\Delta E) (\Delta t) \ge \frac{h}{2 \pi}}
$$

由于 $\frac{h}{2 \pi}$ 这个量经常使用, 其被分配一个符号 $\hbar$ (“h-bar”):

$\hbar = \frac{h}{2 \pi} = \frac{6.626 \times 10^{-34} J \cdot s}{2 \pi} = 1.055 \times 10^{-34} J \cdot s$

34.4 哲学意义; 概率 VS 确定性 Philosophic Implications; Probability Versus Determinism

经典牛顿学说认为世界是确定的. 基本观点为, 一个物体在特定时间的位置和速度是已知的. 如果施加在其上的作用力已知, 其未来的位置可以预测.

而量子力学认为, 物体的速度和位置不能同时精确得知.

由于物质都是由原子构成, 正常的物体也可以用概率表示, 而不是严格的确定. 量子力学预测中, 很大概率普通物体会表现得像经典定律的预测, 因为此时 包含了大量的分子, 此时平均下来, 发生偏差的数量趋近于0.

量子力学中的概率是自然界中固有的.

接受量子力学对自然界的观点被称为 量子力学的哥本哈根解释 (Copenhagen interpretation)

Bohr 认为, 在时间-空间上描述原子和电子的实际运动是不可能的.

34-5 一阶薛定谔方程 – 时间无关形式 The Schrodinger Equation in One Dimension – Time Independent Form

描述 $\psi$ (波函数) 的基本方程就是 Schrodinger equation .

记住一个事实, 这里并没有推导出薛定谔公式, 其只是一种量子力学的解析方法. 这里的式子不过是符合大量的实验情况. 且强加了很多物理意义.

薛定谔方程能写成两种形式:

• 时间相关版本
• 时间无关版本

时间无关版本

其为稳定状态. 此时的波动函数只包括空间依赖. 其用小写的 Ψ (psi) 表示为: $\psi (x)$

经典力学中, 解决问题的两个方法:

• 力的概念和牛顿公式
• 能量的概念和守恒公式

薛定谔方程是基于能量的方法.

描述一个粒子的波 (如, 电子), 其微分方程和经典的波的方程类似, 机械波和电磁波的波的方程如 $A \sin (kx - \omega t)$, $\sin\ 和\ \cos$ 叠加的形式为: $A\sin (kx - \omega t) + B\cos (kx - \omega t)$, 由于这里只与空间相关, 则有 $t=0$, 有:
$$
\displaylines{\psi (x) = A\sin kx + B\cos kx}
$$

(这里 A 和 B 是常量, $k = \frac{2 \pi}{\lambda}$)

对于一个质量为 $m$, 速度为 $v$ 的粒子应用德布罗意波长公式:
$$
\displaylines{k = \frac{2 \pi}{\lambda}, \ \lambda = \frac{h}{p} \newline~ \newline
k = \frac{2 \pi p}{h} = \frac{p}{\hbar}}
$$

利用能量守恒定律:
$$
\displaylines{ \frac{p^2}{2m} + U = E \newline~ \newline
(这里就是动能加势能等于总能量) \newline~ \newline
\frac{\hbar^2 k^2 }{2m} + U = E \newline~ \newline
(用上述公式将 p 替换掉)}
$$

求 $\psi(x)$ 的两次微分:
$$
\displaylines{ \frac{d\psi (x)}{dx} = \frac{d}{dx}(A\sin kx + B\cos kx) = k(A\cos kx - B\sin kx) \newline~ \newline
\frac{d^2 \psi (x)}{dx^2} = k \frac{d}{dx}(A\cos kx - B\sin kx) = -k^2 (A\sin kx + B\cos kx) = -k^2 \psi(x) \newline~ \newline
两边同时乘以\ \frac{-\hbar^2}{2m} \newline~ \newline
-\frac{\hbar^2}{2m} \frac{d^2\psi (x)}{dx^2} = \frac{\hbar^2 k^2}{2m} \psi (x) \newline~ \newline
结合:\ \frac{p^2}{2m} + U = E \newline~ \newline
-\frac{\hbar^2}{2m} \frac{d^2 \psi (x)}{dx^2} + U(x) \psi (x) = E \psi (x)}
$$
这就是 one dimensional time-independent Schrodinger equation. (这里的一维, 就是指这里只考虑了 x 轴的情况)

这里同样有:
$$
\displaylines{ \left\vert \psi \right\vert^2 dV}
$$
表示在体积 $dV$ 中找到一个粒子的概率, 这里由于是一维, 因此 $dV = dx$, 概率之和为:

$$
\displaylines{\int_{all\ spaces} \left\vert \psi \right\vert^2 dV = \int \left\vert \psi \right\vert^2 dx = 1}
$$

这被叫做 normalization condition .

34.6 时间相关的薛定谔方程 Time-Dependent Schrodinger Eequation

time-dependent Schrodinger equation, 公式为:

$$
\displaylines{- \frac{\hbar^2}{2m} \frac{\partial^2 \Psi (x,t)}{\partial x^2} + U(x) \Psi(x,t) = i\hbar \frac{\partial \Psi (x,t)}{\partial t}}
$$
(这里的 $i=\sqrt{-1}$, 为复数, 且此处同样是一维的, 同时注意这里既有对时间的微分, 也有对空间的微分)

用时间相关薛定谔方程得到时间不相关薛定谔方程

$$
\displaylines{\Psi (x,t) = \psi (x) f(t) \newline~ \newline
将其带入上式得: \newline~ \newline
\frac{\hbar^2}{2m} f(t) \frac{\partial^2 \psi (x)}{\partial x^2} + U(x) \psi(x) f(t) = i\hbar \psi (x) \frac{\partial f(t)}{\partial t} \newline~ \newline
两边同时除以 \psi (x) f(t) 得: \newline~ \newline
\frac{\hbar^2}{2m} \frac{1}{\psi (x)} \frac{\partial^2 \psi (x)}{\partial x^2} + U(x) = i\hbar \frac{1}{f(t)} \frac{\partial f(t)}{\partial t}}
$$
此时, 方程的左边只有 x, 方程的右边只有 t. 当左右两边都等于一个常量时, 两边相等, 即:

$$
\displaylines{\frac{\hbar^2}{2m} \frac{1}{\psi (x)} \frac{\partial^2 \psi (x)}{\partial x^2} + U(x) = C \newline~ \newline
i\hbar \frac{1}{f(t)} \frac{\partial f(t)}{\partial t} = C}
$$

上式两边同时乘以 $\psi (x)$ 就变成了薛定谔的时间无关形式 (此时的 C 的值等于 E):
$$
\displaylines{\frac{\hbar^2}{2m} \frac{d^2 \psi (x)}{dx^2} + U(x) \psi (x) = C \psi (x)}
$$

因此下式中的 $C = E$, 有:

$$
\displaylines{ \frac{df(t)}{dt} = -i \frac{E}{\hbar} dt \newline~ \newline
\frac{df(t)}{f(t)} = -i \frac{E}{\hbar}dt \newline~ \newline
\ln f(t) = -i \frac{E}{\hbar} t \newline~ \newline
f(t) = e^{-i ( \frac{E}{\hbar})t}}
$$

因此:
$$
\displaylines{\Psi (x,t) = \psi (x) f(t) \newline~ \newline
= \psi (x) e^{-i ( \frac{E}{\hbar})t}}
$$

由于 $\Psi$ 中包含 $i = \sqrt{-1}$, 其无法直接物理测量, 但 $i^2 = 1$, 因此 $ \left\vert \Psi \right\vert^2$ 可以物理测量,

由于:

$$
\displaylines{ \left\vert f(t) \right\vert = \left\vert e^{-i (\frac{E}{\hbar}) t} \right\vert \newline~ \newline
e^{-i \theta = \cos \theta - i\sin \theta} \newline~ \newline
\left\vert f(t) \right\vert = 1 \newline~ \newline
\therefore \left\vert \Psi (x,t) \right\vert^2 = \left\vert \psi (x) \right\vert^2}
$$

34.7 自由粒子; 平面波和波包 Free Particles; Plane Waves and Wave Packets

34.8 无限深方势阵中的粒子 (一个刚性盒子) Particle in an Infinitely Deep Square Well Potential (a Rigid Box)

之所以建立这个模型, 是因为它可以用来解释许多量子力学的基本概念，如波函数、能级、量子态等.

无限深方势阱（Infinite Square Well）是量子力学中最简单的模型之一，它是由两个无限高的势垒所夹成的一段区域，内部势能为零.
( 关于为什么内部势能为零, 粒子在其中的运动不受势能限制, 势能是一个物体或系统由于其位置、状态或形状而具有的能量, 其与作用于系统的力或场有关, 而这个井内部相当于没有场的作用, 如重力场, 电场, 因此势能为零 )

薛定谔方程只有在几种形式的势能 $U$ 下才能被解出.

考虑两个简单的情况.

第一种情况

质量为 m 的粒子位于一个刚性盒子中:

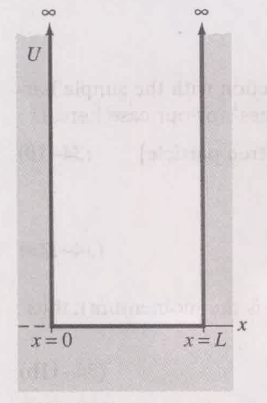
两壁为完全弹性. 且无限深. 势能 $U(x)$ 可以写为:

$$
\displaylines{U(x) = 0,\ 0 < x < L \newline~ \newline
U(x) = \infty,\ x \le 0\ and\ x \ge L \newline~ \newline
(L 为盒子的高度)}
$$
(也就是说, 盒子内势能为0, 盒子外势能为 $\infty$)

在内部, 势能为 0 时, 薛定谔方程的解为:

$$
\displaylines{\psi (x) = A\sin kx + B\cos kx \newline~ \newline
k = \sqrt{ \frac{2m E}{\hbar^2}} \newline~ \newline
(由 \frac{\hbar^2 k^2 }{2m} + U = E, 当 U = 0 时得到 )
}
$$

而外部, 势能为 $U(x) = \infty$ 时, 此时薛定谔方程的解 $\psi (x)$ 一定为零. (不然薛定谔方程中的 $U(x)\psi(x)$ 就不是一个有限值, 也就解不出来了)

求解 A, B 的值以及 k 的限制条件

临界值为, $x=0,\ x=L$, 此时 $\psi = 0$, 有:

$$
\displaylines{\psi (0) = 0\ \ and\ \ \psi (L) = 0 \newline~ \newline
0 = \psi (x) = A\sin 0 + B\cos 0 = 0 + B \newline~ \newline
B = 0 \newline~ \newline
\psi (x) = A\sin kx \newline~ \newline
\because 0 = \psi (L) = A\sin kL \newline~ \newline
A \ne 0 \newline~ \newline
\therefore \sin kL = 0 \newline~ \newline
kL = n \pi, \ \ n = 1,2,3… \newline~ \newline
k = \frac{n \pi}{L} \newline~ \newline
\because k = \sqrt{ \frac{2m E}{\hbar^2}} \newline~ \newline
\therefore E = n^2 \frac{h^2}{8m L^2},\ \ n=1,2,3,…}
$$

这里的 n 被称为 量子数. (其似乎还代表井中的 peak 数量, $n=1$ 时井内为半个周期)

此时可以知道, 刚性盒中的粒子有可以量化的能量. 最低的能量为 (即, $n= 1$):

$$
\displaylines{E_1 = \frac{h^2}{8m L^2}}
$$

由于最低能量不为零, 因此刚性盒中的粒子永远不会静止. 此时 $E_1$ 也被称为 零点能量 (zero-point energy).

在这里, 能量 $E_1$ 和 动量 $p_1 = \hbar k = \frac{\hbar \pi}{L}$ 与刚性盒的边长 $L$ 成反比.

如:

每一个能量状态的波动方程可以写为:

$$
\displaylines{\psi_n = A\sin( \frac{n \pi}{L} x)}
$$

同时有:
$$
\displaylines{1 = \int_{-\infty}^{+\infty} \left\vert \psi \right\vert^2 = \int_0^L A^2 \sin^2 ( \frac{n \pi}{L} x) dx \newline~ \newline
A = \sqrt{ \frac{2}{L}}\ and\ \psi_n = \sqrt{ \frac{2}{L}}\sin ( \frac{n \pi}{L}x)}
$$

这里常有求一段 $x$ 的概率问题, 如 $x \in (0, \frac{L}{3})$, 因此, 这里以 normalization constant 为例:

$$
\displaylines
{
\psi = A \sin \frac{n \pi x}{L} \newline~ \newline
1 = \int_0^L \left\vert \psi \right\vert^2 dx = \int_0^L A^2 \sin^2 \frac{n \pi x}{L} dx \newline~ \newline
let\ \ \theta = \frac{n \pi x}{L} \newline~ \newline
dx = \frac{L}{n \pi} d \theta \newline~ \newline
\therefore 1 = A^2 \int_0^{n \pi} \sin^2 \theta ( \frac{L}{n \pi} ) d \theta = \frac{A^2 L}{2 n \pi} \int_0^{n \pi } (1 - \cos 2 \theta) d \theta \newline~ \newline
= \frac{A^2 L}{2 n \pi} (\theta - \frac{1}{2} \sin 2 \theta ) \vert_0^{n \pi} \newline~ \newline
= \frac{A^2 L}{2}
}
$$

34.9 有限势井 Finite Potential Well

此时的井外的势能是有限的 $U_0$, 不再是无穷大, 但井内的势能仍是 $0$ 这被称为 有限势井 (finite Potential well) .

如下:

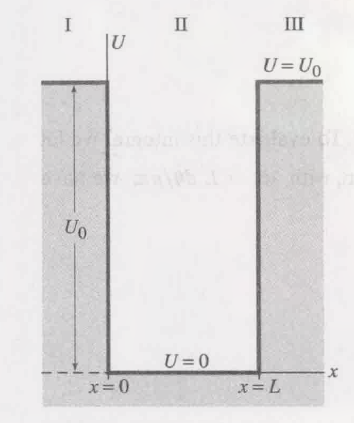
这里分为了三个区域, 在区域二中, 薛定谔方程的解为:

$$
\displaylines
{
\psi_{II} = A\sin kx + B\cos kx\ \ \ (0<x<L)
}
$$

在区域 $I$ 和 $III$ 中, 薛定谔方程中的 $U(x) = U_o$, 则有:

$$
\displaylines
{
\frac{\hbar^2}{2m} \frac{d^2 \psi}{dx^2} + U_0 \psi = E \psi \newline~ \newline
\frac{d^2 \psi}{dx^2} - [ \frac{2m (U_0 - E)}{\hbar^2} ] \psi = 0
}
$$

需要分情况讨论:

先假设 $E < U_0$.

定义一个常量 $G$:

$$
\displaylines
{
G^2 = \frac{2m (U_0 - E)}{\hbar^2}
}
$$

则薛定谔方程可以写为:

$$
\displaylines
{
\frac{d^2 \psi}{dx^2} - G^2 \psi = 0
}
$$

这个方程的通用解为:

$$
\displaylines
{
\psi_{I,III} = C e^{Gx} + D e^{-Gx}
}
$$

当讨论区域 $I$ 时, 由于 $x<0$, 因此 $D=0$, 即 $D$ 一定为零 (不然当 $\psi \rightarrow \infty$ 时, $x \rightarrow -\infty$), 同理, 讨论区域 $III$ 时, 由于 $x0>$, $C$ 一定为零, 最终:

$$
\displaylines
{
\psi_I = C e^{Gx} \ \ (x<0) \newline~ \newline
\psi_{III} = D e^{-Gx} \ \ (x>L)
}
$$

尽管各区域的方程不同, 仍认为波函数是连续的, 其斜率也是连续的.

(曲线表示波函数的值)

此时边界条件 (bound state)的 为:

$$
\displaylines
{
\psi_I = \psi_{II}\ \ and\ \ \frac{d \psi_I}{dx} = \frac{\psi_{II}}{dx}\ \ at x = 0 \newline~ \newline
\psi_{II} = \psi_{III}\ \ and\ \ \frac{d \psi_{II}}{dx} = \frac{\psi_{III}}{dx}\ \ at x = L \newline~ \newline
(从图里面可以看出来)
}
$$

当 $x = 0$ 时, 有:

$$
\displaylines
{
C e^0 = A\sin 0 B\cos 0 \newline~ \newline
\therefore C = B \newline~ \newline
以及 \newline~ \newline
GC e^0 = kA \cos 0 - kB \sin0 \newline~ \newline
\therefore GC = kA
}
$$

对于 infinite well, where the ground-state wave functino is exactly a half wavelength, 有 $\lambda = 2L$, 而对于 finite well, $\lambda > 2L$.

因此, 当 well 有相同宽度 $L$ 时, finite well 中的粒子的动量和基态能量都要小于 infinite well 中的粒子.

在井外 $\psi$ 不为零, 意味着可能能在井外找到粒子. 但是这违背了经典观念, 因为粒子到井外后, 其势能大于总能量 $U_0 > E$, 不符合能量守恒定理.

一个粒子渗透到经典禁止的区域是量子力学的重要结论.

但从测不准原理中:

$$
\displaylines
{
\Delta E \Delta t \ge \hbar
}
$$
可得知能量是不确定的, 因此这里能够不守恒, by an amount $\Delta E$ for very short times $\Delta t \sim \hbar/\Delta E$

又假设 $U_0 < E$

此时能量可以是任何值, 而不是 quantized, 每个区域内的波函数的值都是正弦函数, 但波长不同.

在区域 $II$ 中有:

$$
\displaylines
{
K = \frac{1}{2}m v^2 = \frac{p^2}{2m} \newline~ \newline
\lambda = \frac{h}{p} = \frac{h}{2mE} \ \ 0 < x < L
}
$$

在区域 $I$ 和 $III$ 中有:

$$
\displaylines
{
\frac{p^2}{2m} = K = E-U_0 \newline~ \newline
\lambda = \frac{h}{p} = \frac{h}{\sqrt{2m (E-U_0)}} \ \ x<0\ \ and\ \ x>L
}
$$

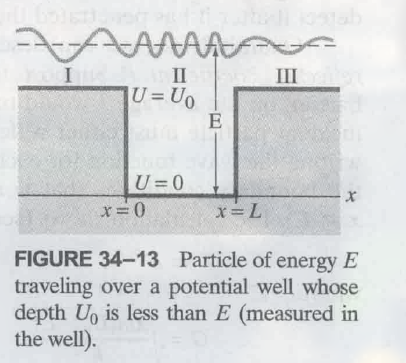
34.10 穿过障碍隧道 Tunneling through a Barrier

在量子力学中, 一个粒子如电子可以穿透障碍渗透到经典力学禁止的区域

考虑一个粒子, 质量为 $m$, 能量为 $E$, 沿着 x 轴在 free space (没有介质, 势能为 0) 中运动, 此时能量等于动能 (E=K), 粒子遇到一个 narrow potential barrier, 高为 $U_0$, 且 $U_0 > E$, 厚度为 $L$.

在经典力学中, 由于 $E < U_0$, 粒子会直接反弹 (因为这个 barrier 是一个经典力学禁止的区域), 但是在量子力学中, 有可能在 barrier 的另一侧发现粒子. 如:

这个过程叫做 穿越障碍 (tunneling through the barrier or barrier penetration)

可以用 传输系数 T(transmission coefficient) 和 反射系数 R (reflection coefficient) 来描述这个过程:

$$
\displaylines
{
T + R = 1 \newline~ \newline
T \approx e^{-2GL} \newline~ \newline
G = \sqrt{ \frac{2m (U_0 - E)}{\hbar^2} }
}
$$

例子, 假设 $T=0.03 \ \ and\ \ R=0.97$, 那么 100 个粒子撞击 barrier, 平均会有 3 个会穿过, 97 个会反弹.

Tunneling 的出现是物质粒子 wave properties 的结果, 也出现在经典波中. 如光穿过玻璃 (?):

Tunneling 的应用

Chapter 35 原子的量子力学 Quantum Mechanics of Atoms

霓虹灯, 就是装气体的管子, 两侧加上高压, 电场会激发稀有气体中的电子，使其跃升到更高的能级。当电子返回原来的能级时，会放出能量以光子的形式发射出光线

35.1 原子的量子力学视角 Quantum-Mechanical View of Atoms

在量子力学的观点下, 电子并不是在特定的轨道上 (do not exist in well-defined circular orbits).

电子由于波的性质, 可以被视为 a “cloud”, 散布在空间中.

电子云也可以看作是概率分布.

给定一个状态的原子, 可以计算其电子云的大小和形状.

电子云也有密度. 其值为 $\left\vert \psi \right\vert^2$.

由于电子云, 原子并没有准确的边界.

电子云是由电子的波的性质的结果.

35.2 氢原子; 薛定谔方程和量子数 Hydrogen Atom; Schrodinger Equation and Quantum Numbers

对于氢原子而言, 其势能可以用电子和质子的库仑力计算:

$$
\displaylines{U = - \frac{1}{4 \pi \epsilon_0} \frac{e^2}{r}}
$$
(毕竟一个氢原子只有一个电子和一个质子, 这里的 r 为质子和电子的距离)

其距离和势能大小的关系图为:

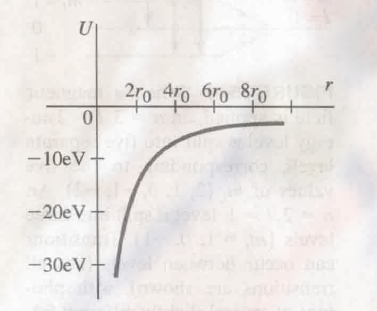
三维的薛定谔方程:

$$
\displaylines{- \frac{\hbar^2}{2m} ( \frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2}) - \frac{1}{4 \pi \epsilon_0} \frac{e^2}{r} \psi = E \psi}
$$

一个量子是对应一个边界条件.

四个量子数

principal quantum number (主量子数), 为:

$$
\displaylines{E_n = -\frac{13.6}{n^2},\ \ n=1,2,3,…}
$$
中的 n. 氢原子在某一状态下的总能量取决于 n.

此时也可以推断出 主量子数确定时不同状态的电子数量为 $2n^2$.

$$
\displaylines
{
N = 2 \sum_{l=0}^{n-1} (2l+1) = 4 \sum_{l=0}^{n-1} l + 2 \sum_{l=0}^{n-1} 1 = 4\frac{(n-1)n}{2} + 2n = 2n^2
}
$$
(毕竟主量子数确定后, 轨道量子数需要取掉所有可以取的值, 然后相加)

orbital quantum number (轨道量子数) 为:

$$
\displaylines{L = \sqrt{l(l+1)\hbar} \newline~ \newline
(L 为轨道角动量)}
$$
中的 $l$, 和电子的轨道角动量的大小相关, 其取值为 $0 \sim (n-1)$ 中的整数, 在氢原子中其不决定总能量, 但当电子数大于等于 2 时, 其和 n 一样影响能量.

此时可知道, 一个 subshell 可容纳的电子数为 $2(2l+1)$ 即 轨道量子数确定时, 不同状态的电子数 .

magnetic quantum number (磁量子数) 为:

$$
\displaylines{L_z = m_l \hbar}
$$
(量子力学中, 角动量的方向通常通过给出其 z 轴的分量来指定, $L_x$ 和 $L_y$ 未定义)
中的 $m_l$, 和电子轨道角动量的方向相关, 其取值为 $-l \sim +l$ 中的整数, $L$ 方向的限制称为 space quantization (空间量化) (可能为, 由于 $m_l$ 为整数, 两个值之间的角度不能取)

注意: $L_z < L$

如:

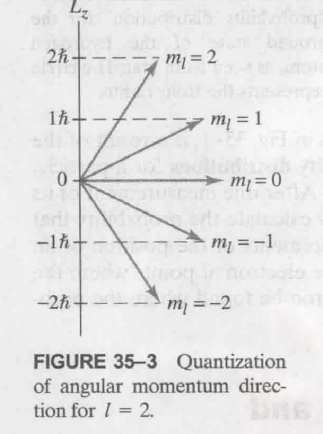
当原子被施加磁场时, 其能量状态不仅取决于 n, 还有 $m_l$. (这也是名字的由来)

如:

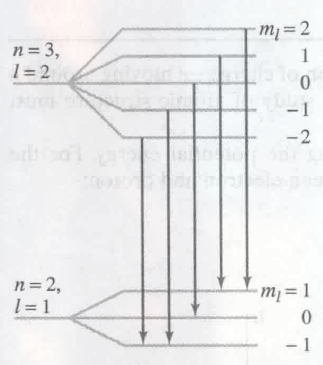
(也就是说, 能量先分为 n 层, 每一层又被 $m_l$ 的取值来划分)

spin quantum number (自旋量子数) 为 $m_s$, 对于一个电子, 其有两个值, $m_s = + \frac{1}{2}\ and\ m_s = -\frac{1}{2}$. (似乎也是代表方向)

电子会绕其轴旋转 (自转).

$$
\displaylines
{
s = \frac{1}{2} \newline~ \newline
S = \sqrt{s(s+1)} \cdot \hbar = \frac{\sqrt{3}}{2} \hbar \newline~ \newline
m_s = \pm \frac{1}{2}
}
$$

35.3 氢原子的波动方程 Hydrogen Atom Wave Function

氢原子基态的波动方程只和 $r$ 相关, 因此其电子云为球对称的. 方程形式为:

$$
\displaylines{\psi_{100} = \frac{1}{\sqrt{\pi r_0^3}} e^{- \frac{r}{r_0}}}
$$
( $r_0$ 是波尔半径, $r_0 = h^2 \epsilon_0/\prime^2 = 0.0529nm$, 下标实际为三个数, $n,l,m_l$ 即 $\psi_{nlm_l}$, 对于基态而言, $n=1,\ l=0,\ m_l=0$)

此时的概率密度为:

$$
\displaylines{ \left\vert \psi_{100} \right\vert^2 = \frac{1}{\pi r_0^3} e^{- \frac{2r}{r_0}}}
$$

能够被标准化 (normalized) 为:

$$
\displaylines{\int_{all\ space} \left\vert \psi_{100} \right\vert^2 dV = 1}
$$

径向概率分布 $P_r$ (radial probability distribution) 表示在 $r \sim r + dr$ 的径向距离内找到电子的概率. (不是某一根线, 而是一个面) 如:

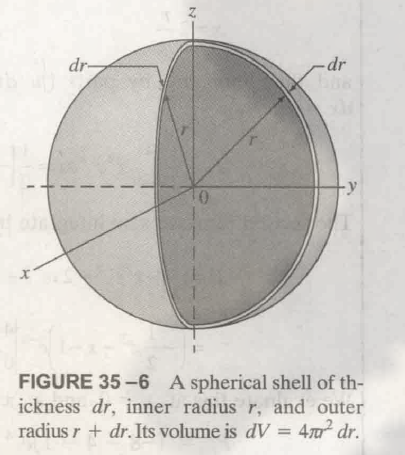
$P_r dr$ 就表示在厚度为 $dr$ 的细壳中找到电子的概率.

细壳的体积为:

$$
\displaylines{dV = 4 \pi r^2 dr}
$$

所以有:

$$
\displaylines{ \left\vert \psi \right\vert^2 dV = \left\vert \psi \right\vert^2 4 \pi r^2 dr}
$$

径向概率分布的值就为:

$$
\displaylines{P_r = 4 \pi r^2 \left\vert \psi \right\vert^2}
$$

对于基态的氢原子, 这个值变为:

$$
\displaylines{P_r = 4 \frac{r^2}{r_0^3} e^{- \frac{2r}{r_0}}}
$$

35.4 复杂的原子; 排他原则 Complex Atoms; the Exclusion Principle

其能级和氢原子不同, 因为电子之间会相互影响, 电子和原子核之间也有相互作用. 此时电子不仅会被原子核吸引, 而且会被其他电子排斥.

对于有多于 1 个电子的原子, 其能级由 $n\ 和\ l$ 一起决定.

中性原子中的电子数被称为 原子序数 $Z$ (atomic number) (由于是中性原子, 电子数等于质子数, 因此此时的质子数也等同于原子序数)

原子序数决定了原子的大部分性质. 其也用来区分各类原子.

泡利不相容原理 (Pauli exclusion principle) : 一个原子中的两个电子不会占据同一个量子态 (No two electrons in an atom can occupy the same quantum state)

电子在原子中占据的量子态由 $n,l,m_l\ and\ m_s$ 决定. (这就是高中讲的轨道) 也就是说, 没有电子有完全相同的一组 $n,l,m_l\ and\ m_s$.

( $m_s = +\frac{1}{2}$ 和 $m_s = - \frac{1}{2}$ 可能就是所谓的上旋和下旋)

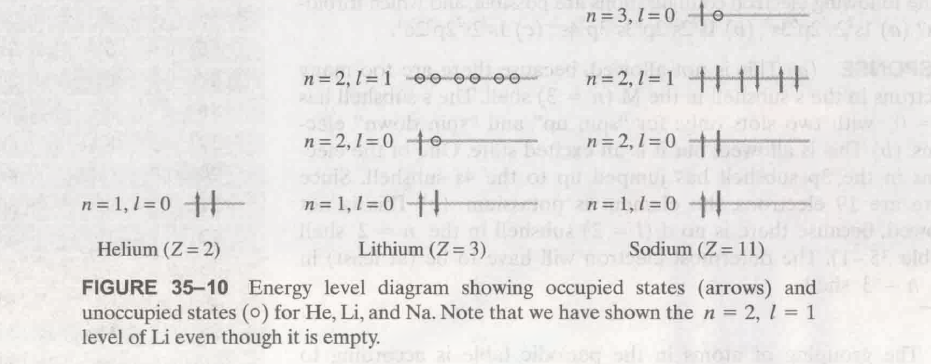
(从这张图看, $n$ 似乎就是轨道号, 能级号)

35.5 元素周期表 The Periodic Table of Elements

如:

具有类似化学性质的元素位于元素周期表的同一列.

每一个格子内包括:

• 原子序数 Z
• 元素符号
• 原子质量

电子的 $n$ 相同表明其位于同一个 Shell, Shell 可以分为 (也就是说 $n$ 的值决定位于哪个 Shell):

1. K Shell (or 1s Shell)
2. L Shell (or 2s, 2p Shell)
3. M Shell (or 3s, 3p, 3d Shell)
4. N Shell (or 4s, 4p, 4d, 4f Shell)

(一共是K,L,M,N,O,P,Q. $n=1$ 在 K Shell, $n=2$ 在 L Shell, $n=3$ 在 M Shell, 以此类推)

电子的 $l$ 的值表明位于哪一个 subshell, 如图:

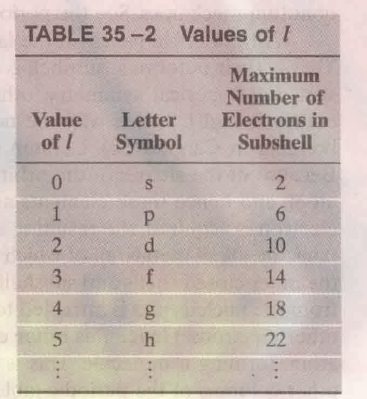
泡利不相容定理, 限制了在同一个 Shell 和 subshell 中的电子数.

在第 $l$ subshell 中, 最多能容纳的电子数为 $2(2l+1)$ (因为 $m_l$ 的可能值有 2l + 1, $m_s$ 的可能值有 2). 如, $l=2$, 那么 $m_l$ 可以取 (2,1,0,-1,-2), $m_s$ 可以取 $+ \frac{1}{2}\ or\ - \frac{1}{2}$.

这个图也告知了每一个 subshell 所能承受的电子个数.

Shell 指的就是: K, L, M, N, O, P…

Subshell 指的就是: s, p, d, f, g

在一个 subshell 中的电子数会以上标的形式写在 subshell 符号上. 如 $1s^2 2s^2 2p^6 3s^1$

一般好像只写出最外层的 subshell 形式, 如:

一个规律, 所有惰性气体 (noble gases) 的 shells 和 subshells 都是装满的状态. 其最外层 subshell 是满的, 电子分布为球对称. 导致外层电子不容易失去, 且不容易吸引电子.

卤素 (halogens), 指 shell 差一个电子装满的元素 (which lack one electron from a filled shell) 容易得到一个电子变为 $-1e$

元素周期表的第一列为碱金属元素 (alkali metals). 容易丢失一个电子成为 $+1e$

subshell 的填装不是一个填满就填下一个.

35.6 X 射线光谱和原子序号 X-Ray Spectra and Atomic Number

原子的线谱是可见的, UV (Ultraviolet, 紫外的) 和 IR (Infrared, 红外的) 部分的 EM (Electromagnetic, 电磁的) 图谱大部分由外层电子状态的迁移导致.

X 射线由, 电子被高压加速后撞击金属靶, 产生.

如图:

$K_{\beta}\ 和\ K_{\alpha}$ 为 peak, 取决于所用的材料. (可以理解为, 加速的电子具有足够的能量使撞击后的电子脱离金属, 不同的金属这样的能量值不同) 因此又被称为 特征 X 射线 (characteristic X-rays)