CAD-考试
考试工具
- 计算器
- 直尺铅笔
电路
两个英语词:
- open circuit 开路
- short circuit 短路
一道题:

其中的:
- $V_{OC}$ 应该指 open circuit 即断路电压
- $V_SC$ 应该指 short circuit 即短路电压
- 同理电流
而戴维南电路求的就是 $\frac{开路电压}{短路电流}$
二阶电路
对于三种阻尼的理解
以弹簧和小球为例解释, 假设有一个弹簧, 上面连着一个小球, 最初弹簧被拉长, 然后回缩:
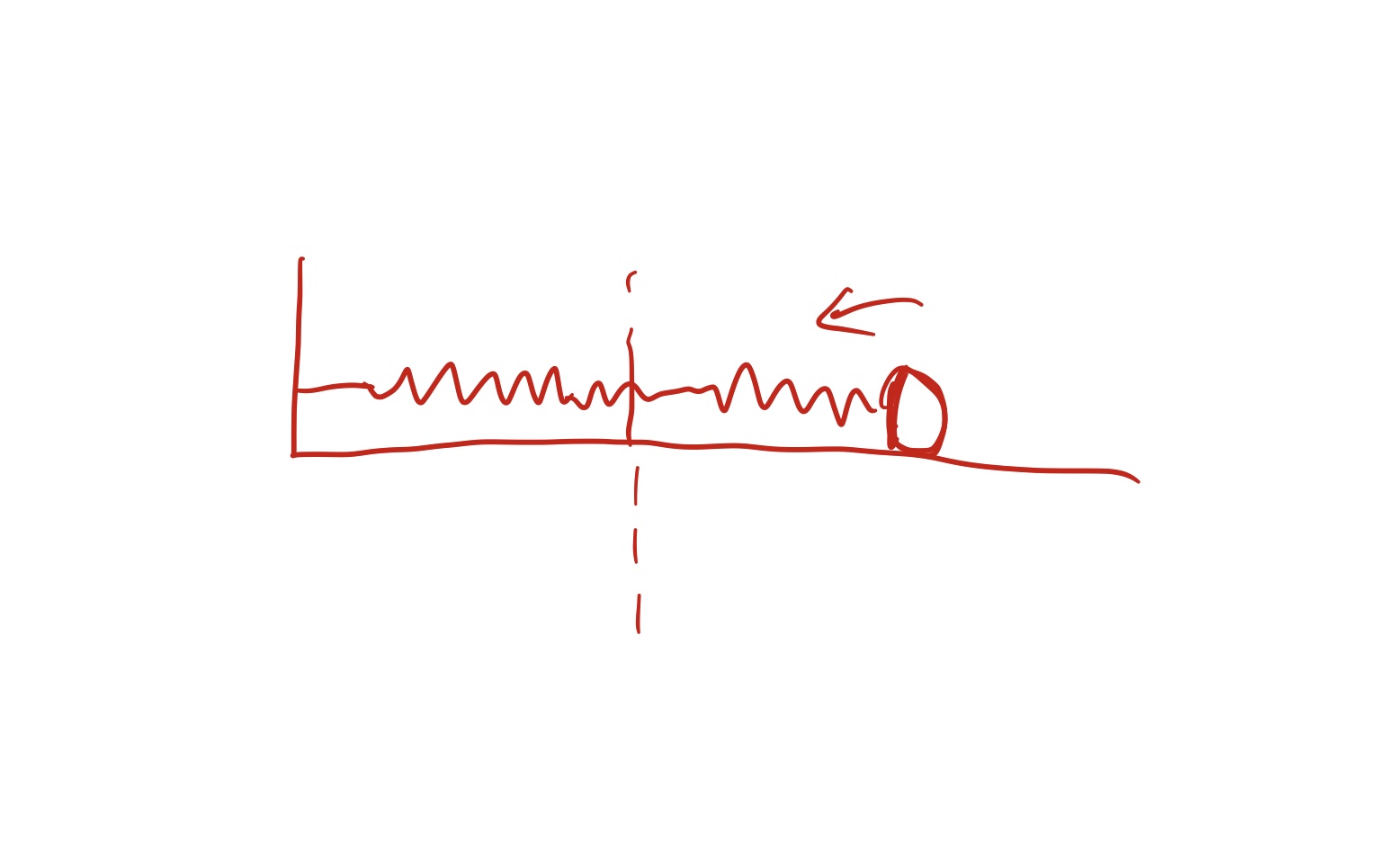
过阻尼 (overdamping) , 即阻力巨大, 以至于还没回到平衡点就停止了:
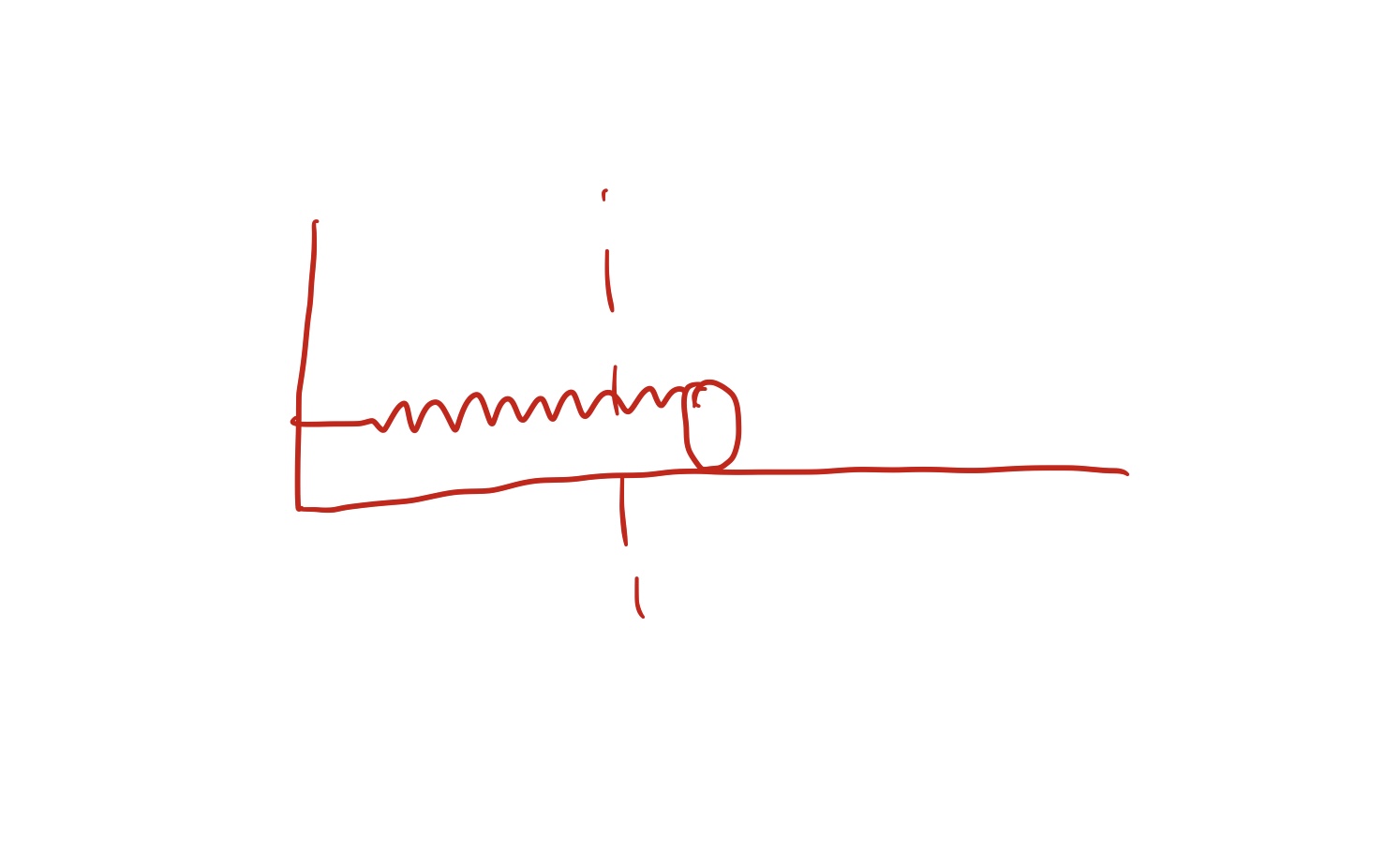
欠阻尼 (underdamped) , 即阻力太小, 过了平衡点还在运动:

临界阻尼 (critical damping) , 指刚好停在平衡点:
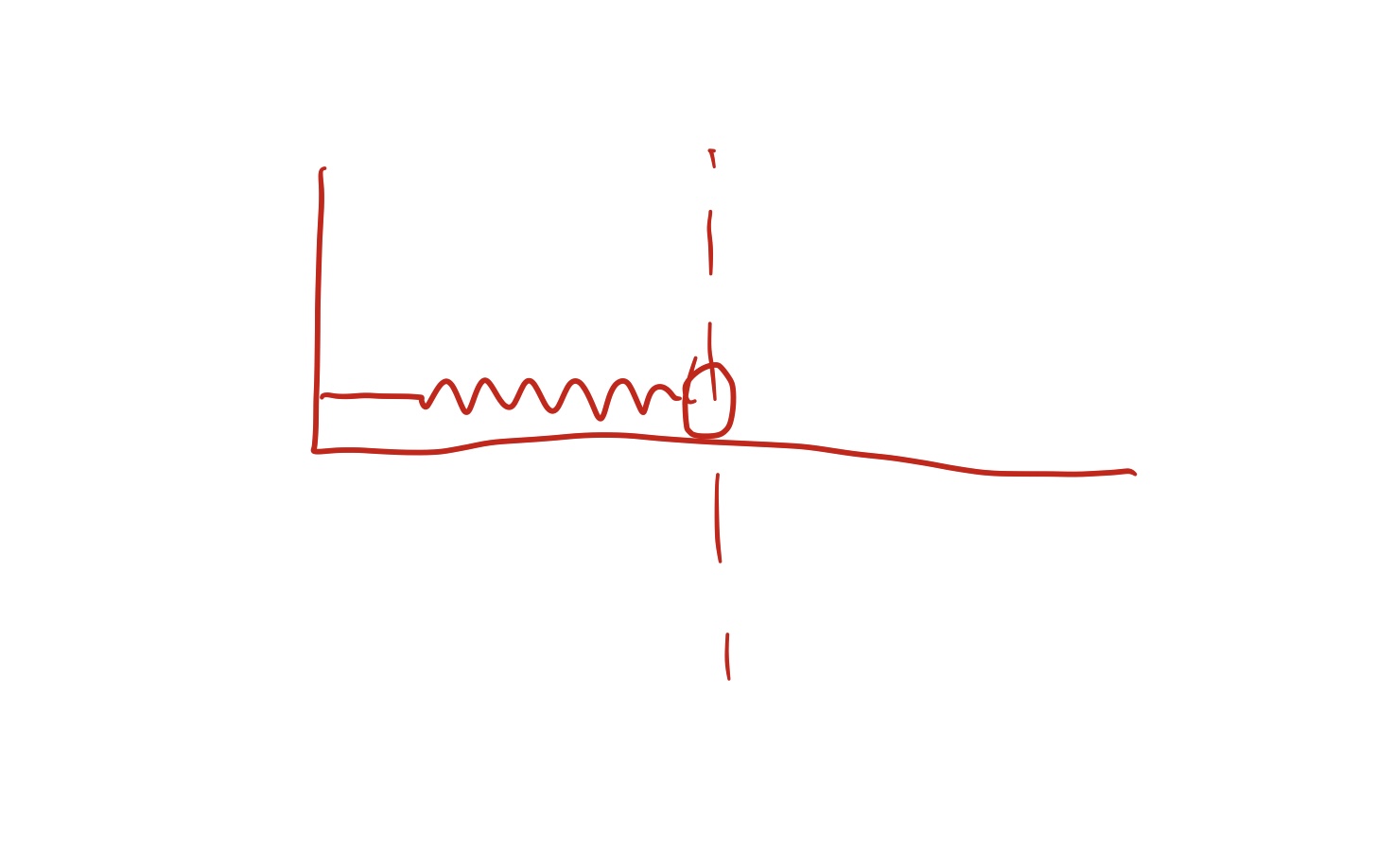
从阻尼这里可以得到振荡的概念, 即能量没有耗散完.
专业一点的解释为:
- overdamping (过阻尼), 永远衰减, 只能无限接近, 永远无法达到真正稳定
- Critical Damped (临界阻尼), 上下两种的临界点, 在稳定状态刚好停住
- underdamped (欠阻尼), 刹不住车, 会出现过冲震荡
储能元件会造成电路阶数的提升, 毕竟能量无法突变, 即功率不会无限大, 需要一定时间传输, 因此获取总的能量就是一个积分.
二阶电路响应
二阶线性微分方程的形式为:
$$
\displaylines
{
v’’ (t) + Av’(t) + Bv(t) = C
}
$$
为什么会觉得困难:
- 微分方程的是函数而不是值
- 微分脱离了基本运算范畴
简化运算, 就使用了 拉普拉斯变换 , 为了将微分, 积分化简为更为基础的运算.
经过拉普拉斯变换有:
$$
\displaylines
{
y’’(t) \rightarrow s^2 y(s) \newline~ \newline
y’(t) \rightarrow sy(s)
}
$$
( 拉普拉斯变换原本并不是为了解微分方程而发明的, 而是恰好发现其用来解微分方程很容易, 而拿过来用 )
傅里叶变换 Fourier Transform
原理: 满足一定条件的信号可以由许许多多个不同频率和相位的 $\cos$ 函数叠加而成.
功能和目的 : 将随横坐标时间 $t$ 变化的时域信号转化为横坐标为 $\cos$ 频率 $\omega$ 的频域信号
条件 : 需满足狄利克雷条件
- 有限个间断点
- 有限个极值点
- 绝对可积, 即 $\int_{-\infty}^{+\infty} \left\vert y(t) \right\vert dt < \infty$
时域到频域转换的示意图:
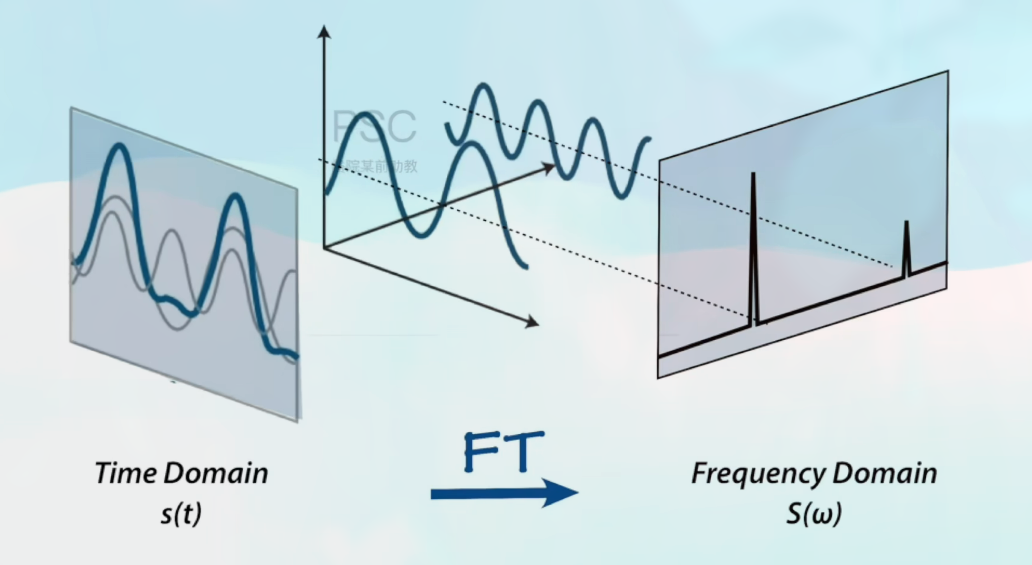
理解如下:
首先左边的图, 灰色的两个波表示两个正弦波, 虽然其频率和振幅都不同, 但加起来等于目标信号, 即蓝色的正弦图.
三维坐标的 $x,y$ 轴用来表示正弦波的频率和振幅(时域), 而 $y,z$ 轴也用来表示正弦波的频率和振幅. (频域)
右边的图, 这个轴, 往左边表示频率低, 往右边表示频率高, 尖端高表示振幅大, 尖端低表示振幅小. 通过尖端来反应其原来是那一个正弦函数. 将这两个尖端和位置相加就相当于将原来的正弦函数相加 (同样有了频率和振幅的信息).
傅里叶变换的好处就在于, 如下:
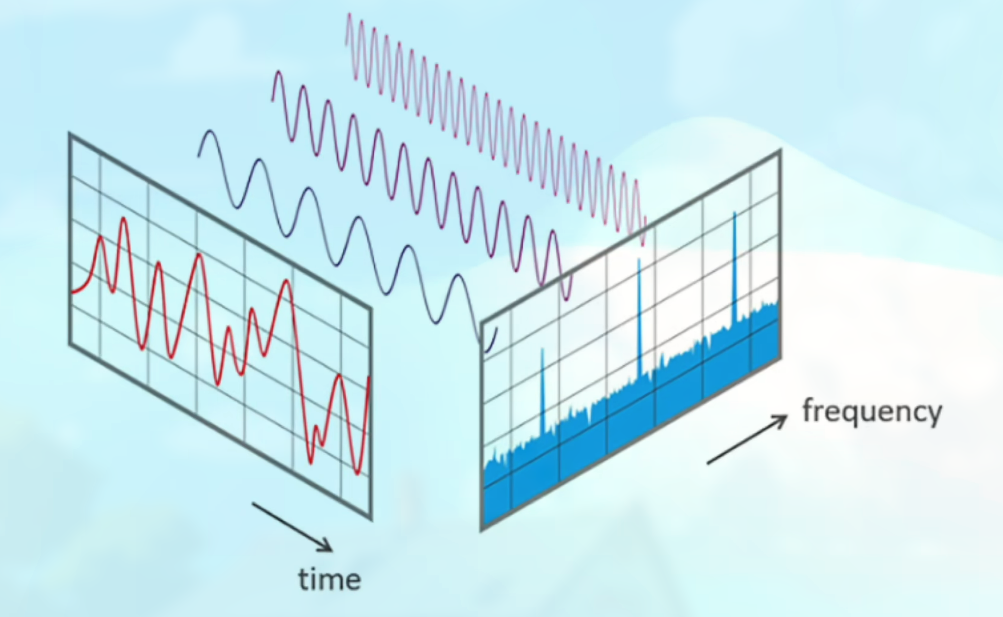
将左边复杂的信号变为右侧三个尖峰. (很直观感觉到变简单了)
转换到频域的好处
如图:
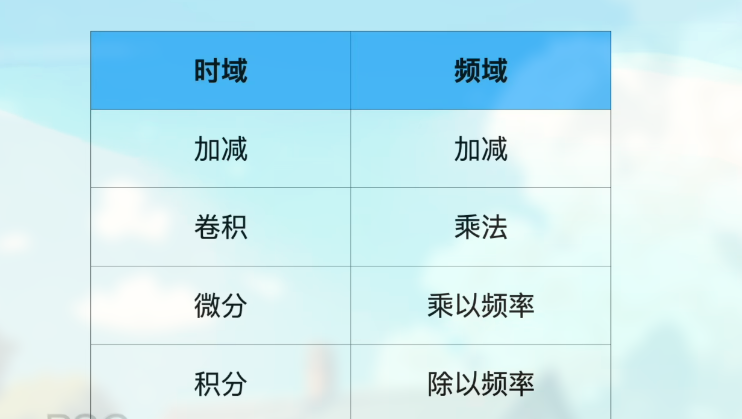
为了将一个函数可以变得可积, 使其可以满足傅里叶变换的条件, 如指数, 增长速度很快:
$$
\displaylines
{
e^{kt}
}
$$
为了使其增长变慢:
$$
\displaylines
{
e^{kt} \overset{\times e^{-\sigma t}}{\rightarrow} e^{(k-\sigma)t} \newline~ \newline
\sigma > k
}
$$
此时这个函数就是一个减函数, 就变为可积了.
这里的 $e^{-\sigma t}$ 就被称为 衰减因子 ( $e^{kt}$ 这样大的函数都能够由这个衰减因子变为减函数, 其他比 $e^{kx}$ 小的函数都可以由其变为减函数 )
此时这些函数就都可以进行傅里叶变换了.
而这个乘以衰减因子再进行傅里叶变换的过程就称为拉普拉斯变换.
拉普拉斯变换表, 如:
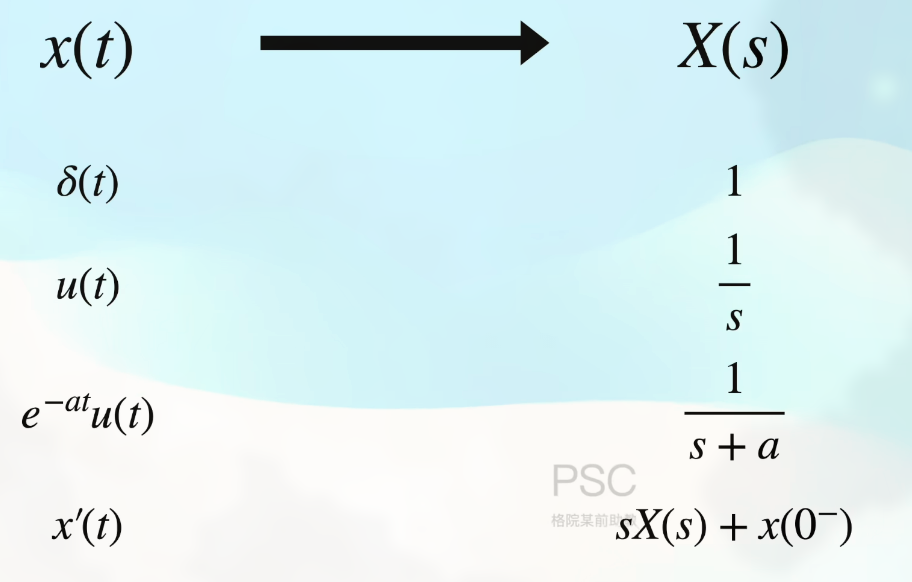
方便记忆 , 求导就是乘以 $s$.
利用拉普拉斯变换求二阶微分方程
方程如:
$$
\displaylines
{
y’’(t) + ay’(t) + by(t) = cu(t)
}
$$
利用拉普拉斯变换转换为频域得:
$$
\displaylines
{
s^2 Y(s) + asY(s) + bY(s) = \frac{c}{s}
}
$$
可以直接解出 $Y(s)$:
$$
\displaylines
{
Y(s) = \frac{c}{s(s^2 + as + b)}
}
$$
利用列项等方法, 得到:
$$
\displaylines
{
Y(s) = \frac{A}{s} + \frac{B}{s + s_1} + \frac{C}{s+ s_2}
}
$$
此时这个函数就容易利用拉普拉斯反变换进行变换 (查表):
$$
\displaylines
{
y(t) = Au(t) + Be^{s_1 t} u(t) + C e^{-s_2 t} u(t)
}
$$
正弦响应
稳态分量记忆方法: 由于是 RL 电路, 因此分母中既有 R 也有 L, 有根号就有平方, 当然, 分子还需要有 $V_m$
Sample 试卷
下图中:
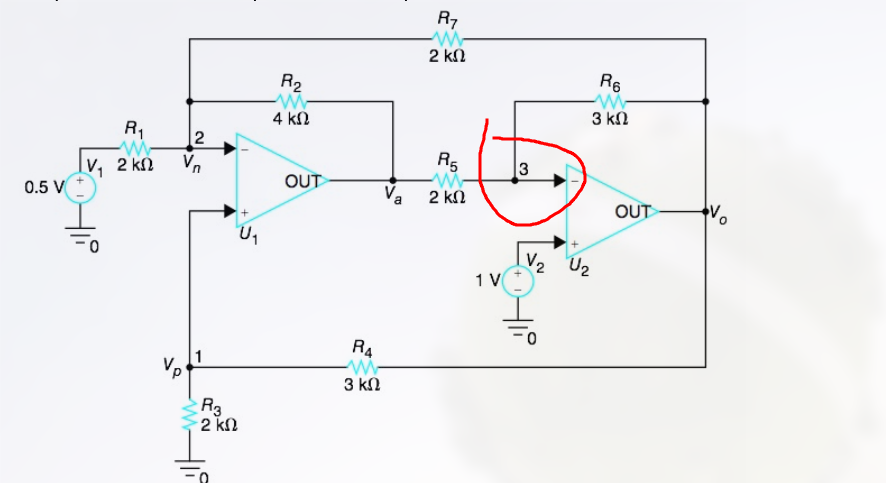
节点 3 处的电势并不为 0, 而是等于 $V_2$.
大题有三个: 普通电路利用节点电压法和网孔电流法分析, 选聘电路, 放大电路.
2022 Dec 试卷
impedance 指阻抗.
transient event 指瞬态事件.
inductor 指电感.
generic circuit 指通用电路.
resonant frequency 谐振频率. 也就是中心频率.
会考带通和帶阻滤波器, RLC 电路.
2022 Jan 试卷
注意 angular frequency 的单位为 $rad/s$
Plot the magnitude response and phase response in linear scale 的意思就是画:
- $\left\vert H(j \omega) \right\vert$
2020 Dec 试卷
illustrating 为 “说明”.
考点:
- 冲激函数
- 电阻串并联
- Kirchhoff
- 电路结构
- 电容电感
- 相量
- Lenz’s law
- 电容电感
充电和放电时, 电容和电感两端的电流和电压都不是瞬间变化的.
instantaneous power 指瞬时功率.
invering configuration 指反相放大器.
noninverting configuration 指正相放大器.
选频电路
stopband 应该指阻带.
corner frequency (null frequency) 似乎也是中心频率 $\omega_o$ 的意思.
RLC 电路的中心频率似乎都是
$$
\displaylines
{
\omega_o = \frac{1}{\sqrt{LC}}
}
$$
关于 phase response 的求法:
如:
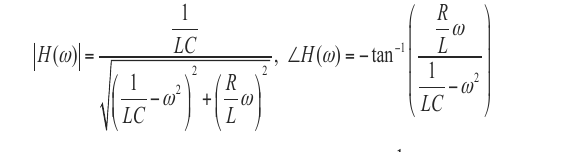
求反 tan, 参数为, 幅值分母的, 频域部分除以时域部分. 另外的规律, phase response 的第一个系数.
对于串联 RLC 来说, 顺序为:
- $C \rightarrow 0$
- $R \rightarrow \frac{\pi}{2}$
- $L \rightarrow \pi$
对于并联 RLC 来说:
- $C \rightarrow -\frac{\pi}{4}$
- $R \rightarrow \frac{\pi}{4}$
- $L \rightarrow \frac{3\pi}{4}$
求 3-dB cutoff frequency 的意思就是求截止频率.
大致规律, 已知转移函数后可用, 如:
$$
\displaylines
{
H( \omega ) = \frac{- \omega^2}{- \omega^2 + \frac{1}{RC} j \omega + \frac{1}{LC}}
}
$$
将分母传统的一元二次方程, 如:
$$
\displaylines
{
a s^2 + b s + c
}
$$
那么截止频率为:
$$
\displaylines
{
\omega_{c1} = -\frac{b}{2} + \frac{b}{2} \sqrt{ \frac{4c}{b^2} + 1} \newline~ \newline
\omega_{c2} = \frac{b}{2} + \frac{b}{2} \sqrt{ \frac{4c}{b^2} + 1}
}
$$
求 3-dB bandwidth 就是求带宽.
串联 求3-dB bandwidth 的公式为:
$$
\displaylines
{
\omega_{3dB} = \omega_2 - \omega_1 = \frac{R}{L}
}
$$
(也就是幅值分母的虚部)
并联为:
$$
\displaylines
{
\omega_{3dB} = \omega_2 - \omega_1 = \frac{1}{RC}
}
$$
响应曲线的大致画法
形状都为 z/倒z 型.
幅值响应曲线, 纵轴范围为 $0 \sim 1$, 横轴为频率. 如:
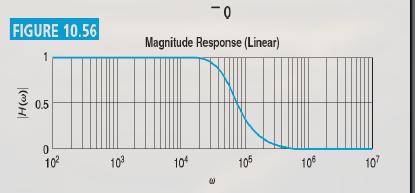
相位响应曲线 , 横轴范围看情况, 一共 $180^\circ$, 最大值由第一个参数决定, 如:

三种阻尼响应
解法都是取 $v(0+)$ 以及 $\frac{dv(0+)}{dt}$, 但方程的形式不同.
过阻尼
$$
\displaylines
{
v(t) = A_1 e^{s_1 t} + A_2 e^{s_2 t} \newline~ \newline
s_1 = - \alpha + \sqrt{ \alpha^2 - \omega^2 } \newline~ \newline
s_2 = - \alpha - \sqrt{ \alpha^2 - \omega^2 } \newline~ \newline
\alpha = \frac{1}{2 RC} \newline~ \newline
\omega_0^2 = \frac{1}{LC}
}
$$
欠阻尼
$$
\displaylines
{
v(t) = B_1 e^{ - \alpha t } \cos \omega_d t + B_2 e^{ - \alpha t } \sin \omega_d t \newline~ \newline
\omega_d = \sqrt{\omega_0^2 - \alpha^2
} }
$$
临界阻尼
$$
\displaylines
{
v(t) = D_1 t e^{- \alpha t} + D_2 e^{- \alpha t}
}
$$