大物考试
19 章
A line of charge
如: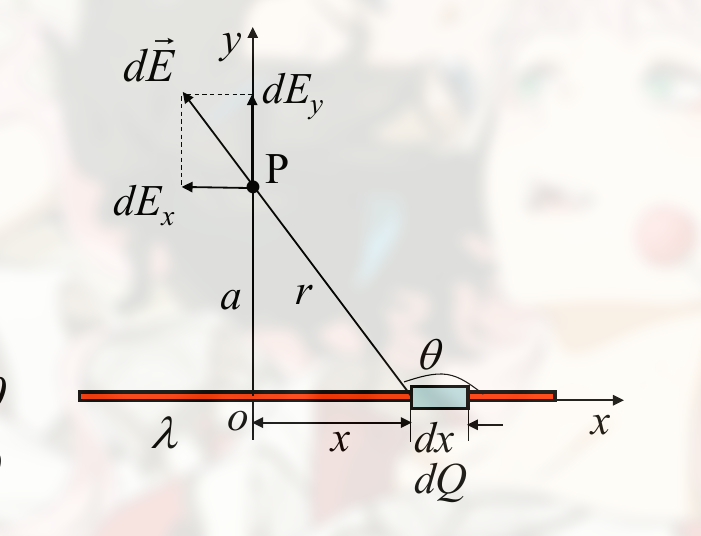
解法
对线段的一小段积分. 算 $dQ$
结论
$$
\displaylines
{
E_y = \frac{\lambda}{4 \pi \epsilon_0 \alpha} ( \cos \theta_1 - \cos \theta_2 )
}
$$
如果无限长, 那么 $\theta_1 = 0$, $\theta_2 = \pi$, 则有:
$$
\displaylines
{
E_x = 0 \newline~ \newline
E_y = \frac{\lambda}{2 \pi \epsilon_0 a}
}
$$
A plane of charge
如:
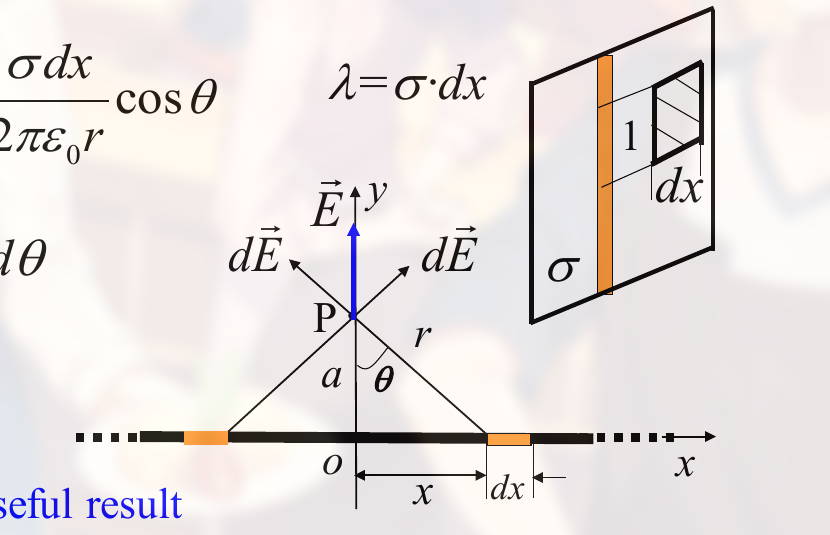
解法
先算环, 再算平面.
有:
$$
\displaylines
{
E = \frac{\sigma}{2 \epsilon_0}
}
$$
Uniformly charged ring
如:
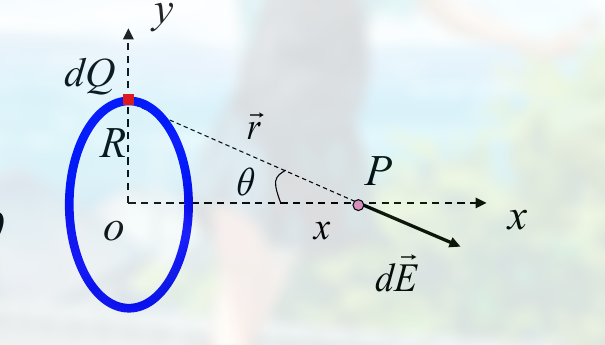
解法
算环的一段的电荷, $dQ$
有:
$$
\displaylines
{
E = \frac{Q \cdot x}{4 \pi \epsilon_0 ( x^2 + R^2 )^{3/2}}
}
$$
Uniformly charged disk
如:
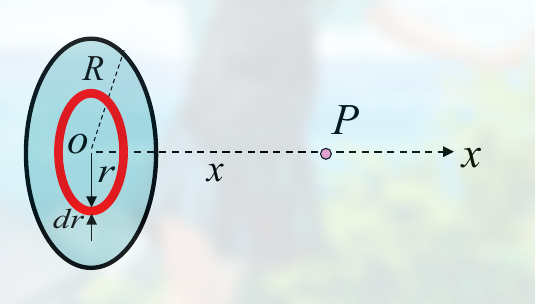
解法
同样是先求环, 再求面
有:
$$
\displaylines
{
E = \frac{\sigma}{2 \epsilon_0} [ 1 - \frac{x}{\sqrt{ x^2 + R^2 }} ]
}
$$
Parallel-plane capacitor
如:
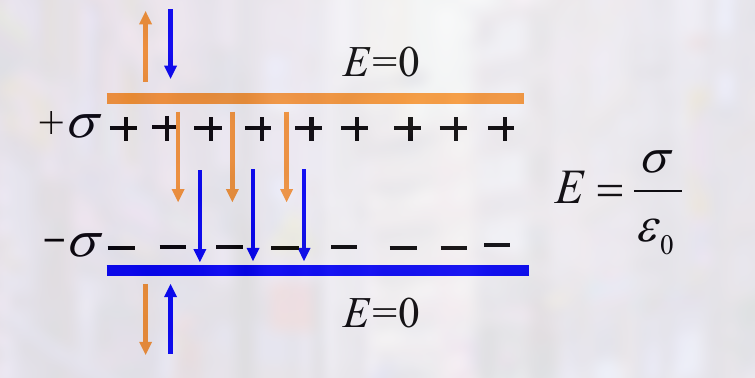
解法
先求一个面, 在将两个面整合
有:
$$
\displaylines
{
E = \frac{\sigma}{\epsilon_0}
}
$$
33 章
Hydrogen atom in $3^{rd}$ excited state, how many types of photon can it emit?
4 种.

34 章
注意:
$$
\displaylines
{
P_1 = \left\vert \Psi_1 \right\vert^2 \newline~ \newline
P_2 = \left\vert \Psi_2 \right\vert^2 \newline~ \newline
P_{12} = \left\vert \Psi_1 + \Psi_2 \right\vert^2 \newline~ \newline
\ne P_1 + P_2
}
$$
干涉和衍射
下面的题大概可以用这张图解释:
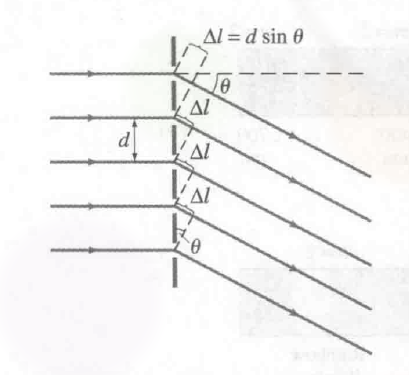
光栅到屏幕的距离应该就是 $L$, 而 $y$ 应该就是虚线之下的距离.
The peaks of the interference pattern are given by :
$$
\displaylines
{
d \sin \theta = m \lambda,\ \ m=1,2,… \newline~ \newline
(d \sin \theta 表示的是光程差, 这里就相当于是 \newline~ \newline
光程差的整数倍, 这样才会发生 \newline~ \newline
constructive interference )
}
$$
在屏幕上的位置为:
$$
\displaylines
{
y = L tan \theta
}
$$
对于小角度, 有:
$$
\displaylines
{
\sin \theta \approx \tan \theta
}
$$
因此有:
$$
\displaylines
{
y = m L \frac{\lambda}{d}
}
$$
测不准
Calculate the uncertainty in position. 指的是测量位置的 uncertainty.
题中出现 “measured to an accuracy of 0.065 persent” 的含义, 如下题:
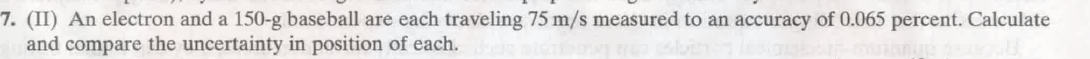
其意思就是:
$$
\displaylines
{
\frac{\Delta v}{v} = \frac{0.065}{100}
}
$$
问如 what fraction of the transition energy is this
就是求:
$$
\displaylines
{
\frac{\Delta E}{E}
}
$$
两个最重要例题

主要有这样的思路, 比如, 由于 $\Delta p$ 变化太小, 可以将其视作做了一个微分, 也就是 $d$, 就如
这种题就是已知了如 $\frac{\Delta p}{p}$, $\frac{\Delta \lambda}{\lambda}$ 的解法
$$
\displaylines
{
p = (2mK)^{1/2} \newline~ \newline
(接下来两边同时取微分) \newline~ \newline
\Delta p = \frac{1}{2} (2m/K)^{1/2} \Delta K \newline~ \newline
\Delta p / p = \frac{1}{2} \frac{\Delta K}{K}
}
$$
疑惑
薛定谔方程记忆方法
时间无关: 有波函数, 其二阶导.
通过能量守恒得来的, 因此有势能和总能量.
时间相关: 既有时间的微分, 也有位移的微分, 既有一阶导, 也有二阶导, 还有复数
波函数
有一道题让你求波函数, 利用:
$$
\displaylines
{
\psi (x) = A \sin kx + B \sin kx
}
$$
最终结果中, 可以不用求出 $A$ 和 $B$.
无限深
IDSWP 指的就是 Infinite Deep Square Well P
the energy of ground state 指 $n = 1$
the energy of first exited state 指 $n = 2$
在井中的概率, where does the particle have maximum probability densities.
注意概率是求平方, 因此正弦函数为 $\pm 1$ 时最大.
what is the probability to find the particle in reginon?
这个就是利用:
$$
\displaylines
{
\int \left\vert \psi \right\vert dV
}
$$
来求, 在一维上, $dV = dx$
注意, 虽然井中的粒子的最大波长满足:
$$
\displaylines
{
\lambda_{max} = 2L
}
$$
但是, 井中的粒子能发射的波的最大波长应该为从:
$$
\displaylines
{
n_2 = 2 \ \ to\ \ n_1 = 1
}
$$
的时候.
within $\frac{1}{4}L$ of either wall 的意思是离墙的距离为 $\frac{1}{4}L$ 的区域
classical prediction, 表示
电子在井中的任何位置出现的概率相同. 即如果 $0 \sim \frac{1}{2}L$ 出现的概率为 $50%$ 那么在 $\frac{1}{2}L \sim L$ 处出现的概率也是 $50%$
有限深
35
状态数
若给定了 $n = 2$, 那么可以得出:
$$
\displaylines
{
l = 0,1 \newline~ \newline
m_l = -1,0,1 \newline~ \newline
m_s = \pm \frac{1}{2}
}
$$
共有的情况为:
$$
\displaylines
{
1 \times 2 + 3 \times 2 = 8
}
$$
题中若为 write down the quantum numbers for each state, 写法为:
$$
\displaylines
{
(n, l, m_l, m_s)
}
$$
注意 , $l = 0$ 时, 位于的 subshell 为 $s$
通过 $6g$ 可以推断出 $n = 6$, 且 $l = 4$.
氢原子的波函数
对于基态而言, 有波函数:
$$
\displaylines
{
\psi_{100} = \frac{1}{\sqrt{\pi r_0^3}} e^{ - \frac{r}{r_0} }
}
$$
其中 $r_0$ 为波尔半径:
$$
\displaylines
{
r_0 = \frac{h^2 \epsilon_0 }{\pi m e^2} = 0.0529nm
}
$$
概率密度计算为:
$$
\displaylines
{
\left\vert \psi_{100} \right\vert^2
}
$$
Radial probability distribution 计算为:
$$
\displaylines
{
\left\vert \psi \right\vert^2 \cdot 4 \pi r^2 dr = P_r dr \newline~ \newline
P_r = 4 \pi r^2 \left\vert \psi \right\vert^2 = \frac{4 r^2}{r_0^3} e^{- \frac{2r}{r_0}}
}
$$
(似乎这就是计算出现在某个体积内的概率)
往年试卷
选择题
必有 RLC 电路.
必有一道洛伦兹变换.
Q_2 (a) (b)
必有无限深井.
注意一些题虽然没有明确的给出物理量的值, 但还是都可以用.
大题构成:
- 两道电磁
- 一道量子力学