概率论考试

排列和组合

$A^c$ 表示 A 的补集.

已知并集和各个概率, 可以求交集 :

如:

条件概率

条件概率的英文为 Conditional Probability.

需理清思路的例题:

易错题:

有两种解法.

我们要求的往往是交集的概率而不是条件概率, 往往已知的条件就是条件概率的值.

做错的题:

equally likely 的意思就是等可能.

做错例题:

条件概率通常和 partion 一起使用.

独立事件

证明两个事件 independent 就是证明:

$$
\displaylines
{
Pr(AB) = Pr(A) Pr(B)
}
$$

如何证明: A 和 $B^C$ 也是独立的.

相互独立和两两独立

defective item 指有次品.

下题的答案如何推导:

做错的例题:

注意这道题:

由于最后一个位置已经是确定的.

注意 , 互斥并不等价于 mutually independent.

Bayes’ Theorem

下题要求求的量是啥:

随机变量

注意概率密度函数的积分才为 1, 这也意味这:

$$
\displaylines
{
f(x) \le 1
}
$$

同时注意:

$$
\displaylines
{
P(X=3) = \int_1^3 f(x)dx = f(1) + f(2) + f(3)
}
$$

写法上的不同, the binomial distribution with parameters n and p for which the p.f is 写为:

$$
\displaylines
{
f(x|n,p) = \begin{cases}
\binom{n}{x} p^x (1-p)^{n-x},\ \ for x = 0,1,2,…,n \newline~ \newline
0, \ \ otherwise
\end{cases}
}
$$

对于伯努利试验, 常见的提法为: with parameter $p$ if the p.f. of X is $f(x) = p^x (1-p)^{1-x}$ for $x=0,1\ and\ 0$ otherwise.

关于什么是 i.i.d. , 即 independent and identically distributed

累加分布函数

即 cumulative distribution function. 也可以直接称为 分布函数. 也指 c.d.f.

即 $F(x) = Pr(X \le x)$

随机变量函数的分布

离散型

如:

连续型

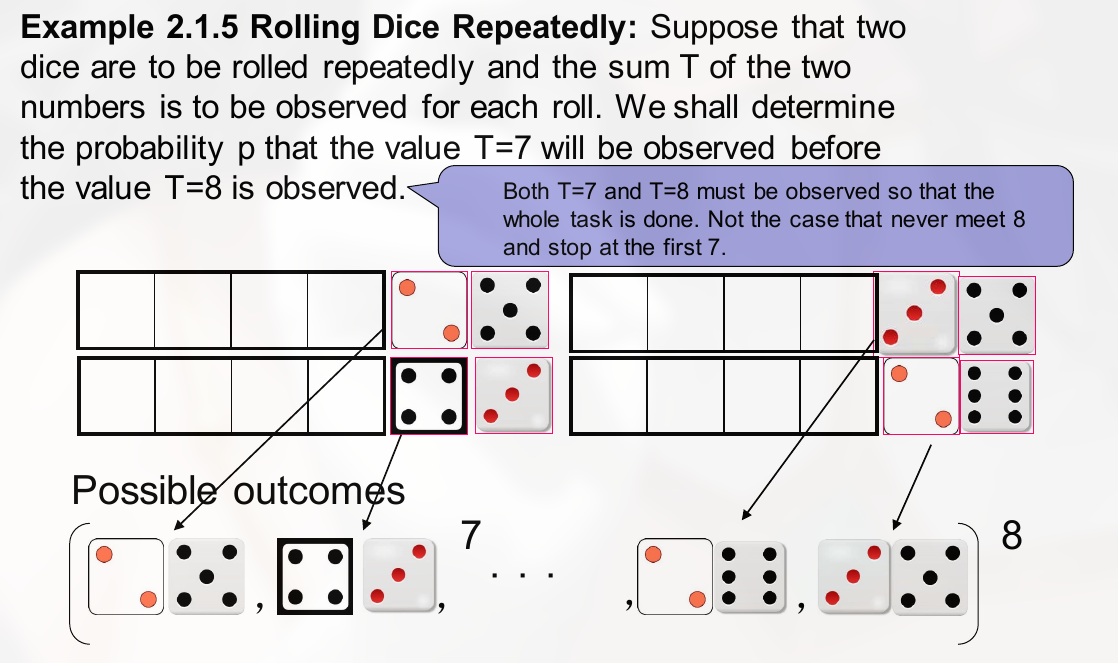
例, x 的密度函数为 $f_x(x)$, 且 $Y = 3X + 2$, 求 Y 的密度函数.

思路:

1. 先写出两者的分布函数, $F_X(x) = P\{X \le x\}$ 和 $F_Y(x) = P\{Y \le x\}$
2. 求导, 注意复合函数

如, 这里以均匀分布为例:

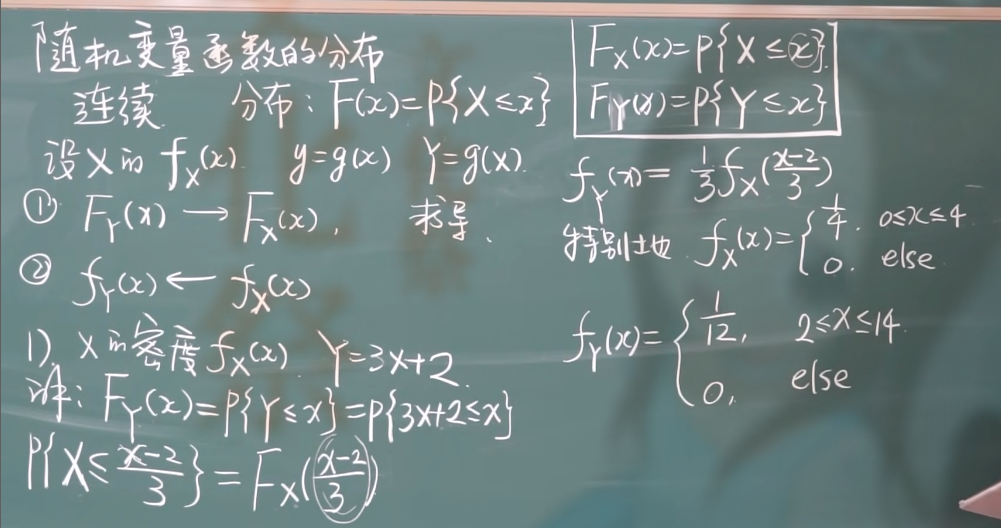
注意将 $X$ 单独弄出来.

注意参数范围的变化。

注意一个坑:

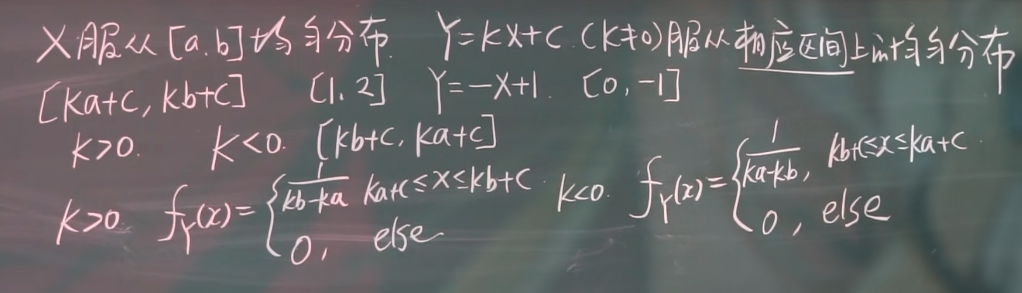
也就是写取值是的坑.

以正态分布为例:

注意 $a$ 的正负.

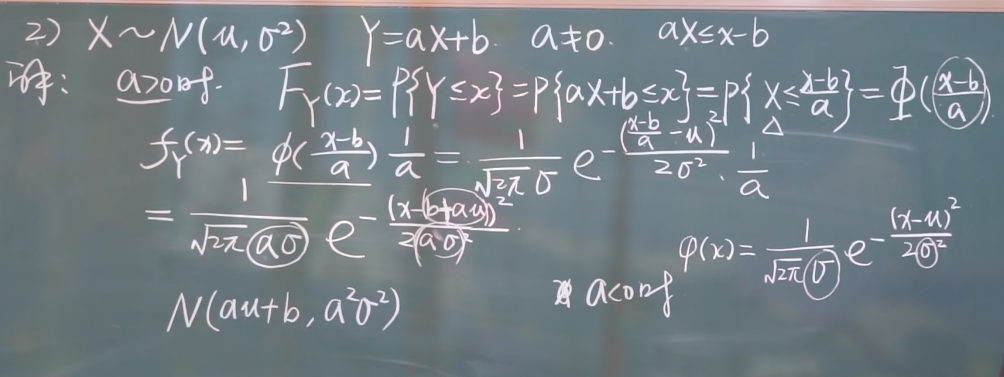
注意新的对称轴和新的方差的求法.

什么是 线性 , 如 $2x + 3y$, $x_1 + x_2 + x_3$ 等

线性式中都要分 $k$ 的正负.

多维随机变量及其分布

联合分布

联合分布指共同.

边缘分布指一个.

一维的分布函数为面积, 二维的分布函数为体积.

性质:

• $F(x,y)$ 不减, y 固定, $x_1 < x_2$, 则 $F(x,y) \le F(x_2,y)$
• $F(-\infty, y) = 0,\ F(x, -\infty)=0,\ F(-\infty,-\infty)=0,\ F(+\infty,+\infty)=1$

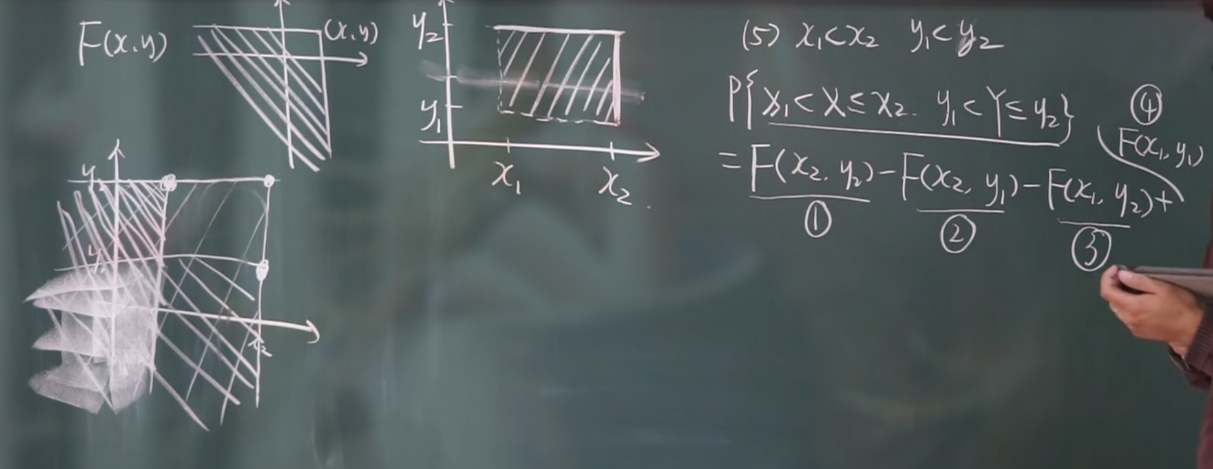
注意画图理解. 注意这里的实线和虚线.

边缘分布

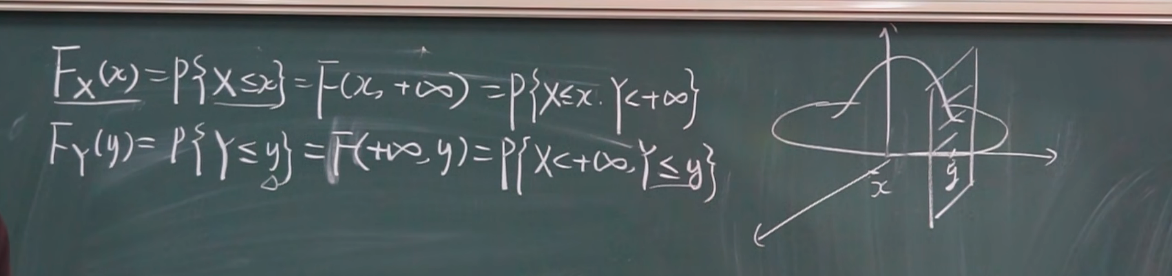
二维随机变量的边缘密度函数

密度函数都用分布函数求导来得到.

如:

$$
\displaylines
{
F_X(x) = F(x, +\infty) = \int_{-\infty}^{x} [\int_{-\infty}^{+\infty} f(s,t)dt] ds
}
$$

则 x 的密度函数为:

$$
\displaylines
{
f_x(x) = \int_{-\infty}^{+\infty} f(x,t)dt = \int_{-\infty}^{+\infty} f(x,y)dy
}
$$

y 的密度函数同理.

理解, 求切面的面积:

上限是函数的积分求导方法:

1. 上限求导
2. 上限带入 t

$$
\displaylines
{
\int_{a}^{f(x)} g(t) dt = f’(x) g(f(x))
}
$$

二元分布

Theater Patrons 指剧院顾客.

discrete joint distribution 指离散联合分布. 这个的求法似乎不能积分, 只能加减.

continuous joint distribution. 用积分.

$$
\displaylines
{
Pr[(X,Y) \in C] = \int \int_C f(x,y) dx dy
}
$$
f 称为 joint probability density function (p.d.f.) of X and Y , The closure of the set $\{(x,y):f(x,y)>0\}$ is called the support of (the distribution of ) (X,Y)

(可以看出, support 似乎就是基本条件)

一个 joint p.d.f. 必须满足的条件:

$$
\displaylines
{
f(x,y) \ge 0\ for\ -\infty < x < +\infty\ and\ -\infty < y < +\infty \newline~ \newline
\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x,y) dxdy = 1
}
$$
(也就是, 密度函数值永远大于等于零, 全部积分结果为1)

做错的题:

注意 , $Pr(X \ge Y)$ 的隐含条件就是 $y$ 的积分的上限为 $x$

当要求的某一个度量是 均匀的 时, 则有, 如:

Mixed Bivariate Distributions:

$$
\displaylines
{
Pr(X \in A\ and\ Y \in B) = \int_B \sum_{x \in A} f(x,y)dy
}
$$

Joint (Cumulative) Distribution Function/c.d.f.

$$
\displaylines
{
F(x,y) = Pr(X \le x\ and\ Y \le y) \newline~ \newline
= \int_{-\infty}^{y} \int_{-\infty}^{x} f(r,s) drds \newline~ \newline
f(x,y) = \frac{\partial^2 F(x,y)}{\partial x \partial y}
}
$$
求偏导的方法, 例:

如下:

$$
\displaylines
{
固定 y 然后求导\newline~ \newline
= \frac{1}{16}y[2x + y] \newline~ \newline
固定 x 然后求导\newline~ \newline
= \frac{1}{16}[2y + 2x] \newline~ \newline
= \frac{1}{8} (x+y)
}
$$

Marginal Distributions

这里的几个叫法:

• $F_1,\ F_2$ are called the marginal c.d.f. of X, and Y, respectively
• marginal p.f. or marginal p.d.f. of X

注意:

$$
\displaylines
{
f_1(x) = \int_{-\infty}^{+\infty} f(x,y)dy\ for\ -\infty < x < \infty \newline~ \newline
f_2(y) = \int_{-\infty}^{+\infty} f(x,y)dx\ for -\infty < y < \infty
}
$$
可以看出, 如第一个式子, 我们一般选中一个 x 的值, 然后将其所有 y 的值积分, 如:
$$
\displaylines
{
f(1) = \int_{-\infty}^{+\infty} f(1,y) dy
}
$$

做错题:

Mixed Bivariate Distributions

指的是, 一个变量连续, 另一个不连续.

如:

独立随机变量 independent random variables

如果说两个随机变量是独立的, 那么有:

$$
\displaylines
{
Pr(X \in A\ and\ Y \in B) = Pr(X \in A) Pr(Y \in B) \newline~ \newline
即: F(x,y) = F_1(x) F_2(y)
}
$$

例题:

注意 , 这里为随便取一组数据来验证.

做错例题:

利用 independent 随机变量的 p.d.f. 来求 c.d.f.

不会的题:

条件分布 Conditional Distributions

形式:

$$
\displaylines
{
g_1 (x|y) = \frac{f(x,y)}{f_2(y)}
}
$$

$g_1$ 被称为 the conditional p.f. of X given Y

而 $g_1(.|y)$ 被称为 the conditional distribution of X given that $Y = y$

例题:

连续的条件分布 (continuous conditional distribution) , 例题:

随机变量的全概率公式 , 注意连续和不连续的写法:

不连续:

$$
\displaylines
{
f_1(x) = \sum_y g_1(x|y)f_2(y)
}
$$

连续:

$$
\displaylines
{
f_1(x) = \int_{-\infty}^{+\infty} g_1 (x|y) f_2(y) dy
}
$$

随机变量的 Bayes’ Theorem :

对于 Y given $X = x$ is:

$$
\displaylines
{
g_2(y|x) = \frac{g_1(x|y) f_2(y)}{f_1(x)} \newline~ \newline
}
$$

对于 X given $Y=y$ is:
$$
\displaylines
{
g_1(x|y) = \frac{g_2(y|x) f_1(x)}{f_2(y)} \newline~ \newline
}
$$

多元变量分布

即 Multivariate Distribution

$$
\displaylines
{
F(x_1,…,x_n) = Pr(X_1 = x_1,…,X_n=x_n) \newline~ \newline
Pr[(X_1,…,X_n) \in C] = \int … \int f(x_1,…,x_n) dx_1…dx_n \newline~ \newline
}
$$

边际分布的示例:

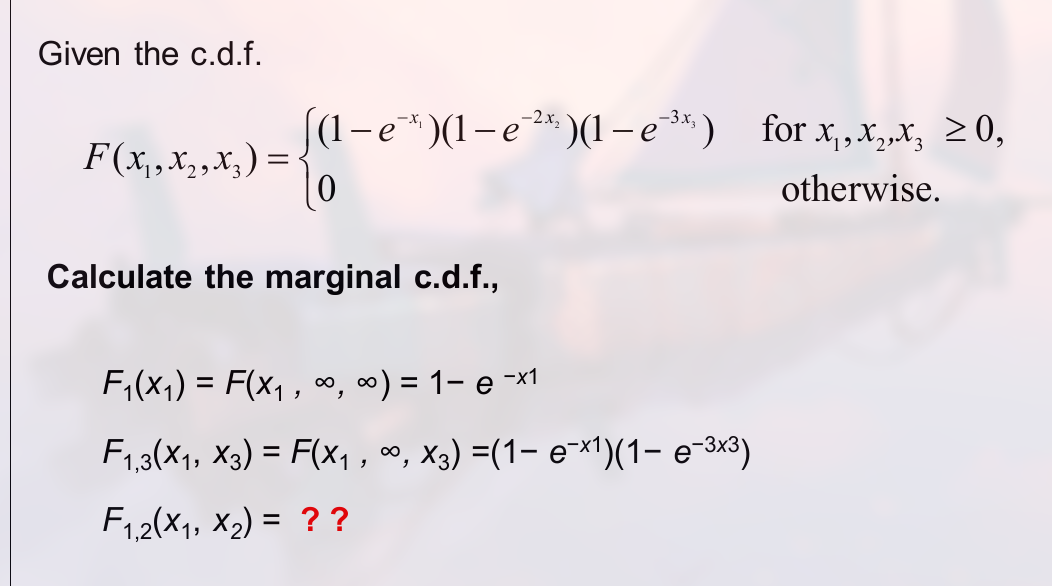
如:

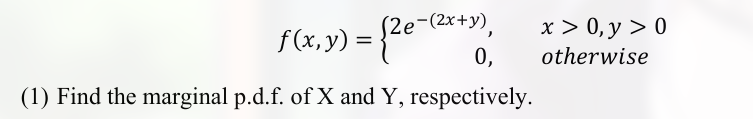
这种题就是直接加一个微分.

随机变量的函数

指一个随机变量是另一个随机变量的函数.

做错的例题:

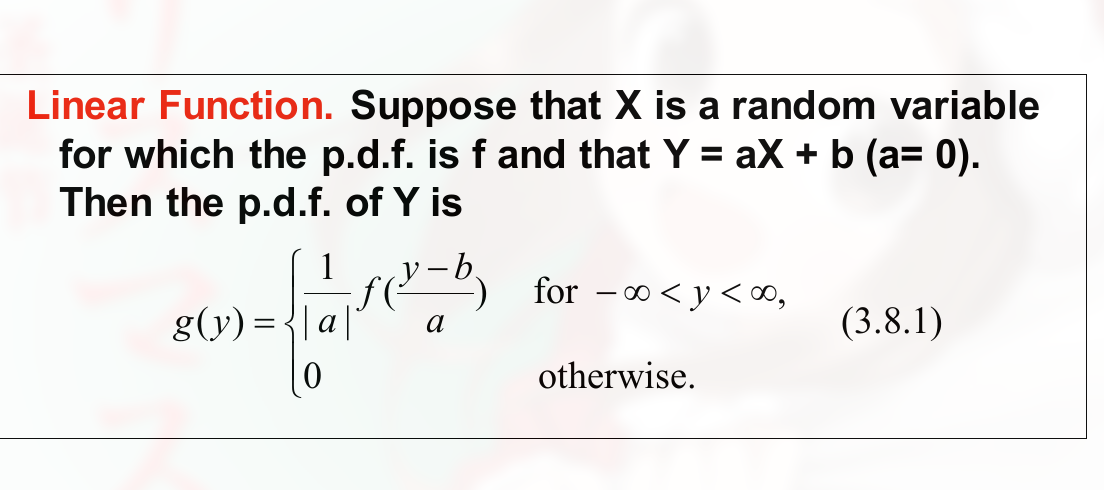
疑惑, 为什么没变方向:

这一章差不多最后 20 页 PPT 不太懂.

卷积公式

只记住一种类型, $X_1$ 和 $X_2$ 独立, $Y = X_1 + X_2$, 此时, Y 的分布就称为 $X_1$ 和 $X_2$ 的分布的卷积 .

联合 p.d.f. (X,Y) 写为 $f(x,y)$, 则有:

$$
\displaylines
{
f_z(Z) = \int_{-\infty}^{+\infty} f_X(x)f_Y(z-x)dx
}
$$

推导

$$
\displaylines
{
F_z(Z) = P\{X + Y \le z\} \newline~ \newline
= \int \int\limits_{x+y \le z} f(x,y)dx dy \newline~ \newline
= \int_{-\infty}^{z-y} [ \int_{-\infty}^{+\infty} f(x,y)dx ]dy
}
$$
化简到这一步后, 再令 $x = \mu - y$, 则

因此, 卷积公式是用来得到一个概率密度函数.

注意这里的例题.

辛普生分布 :

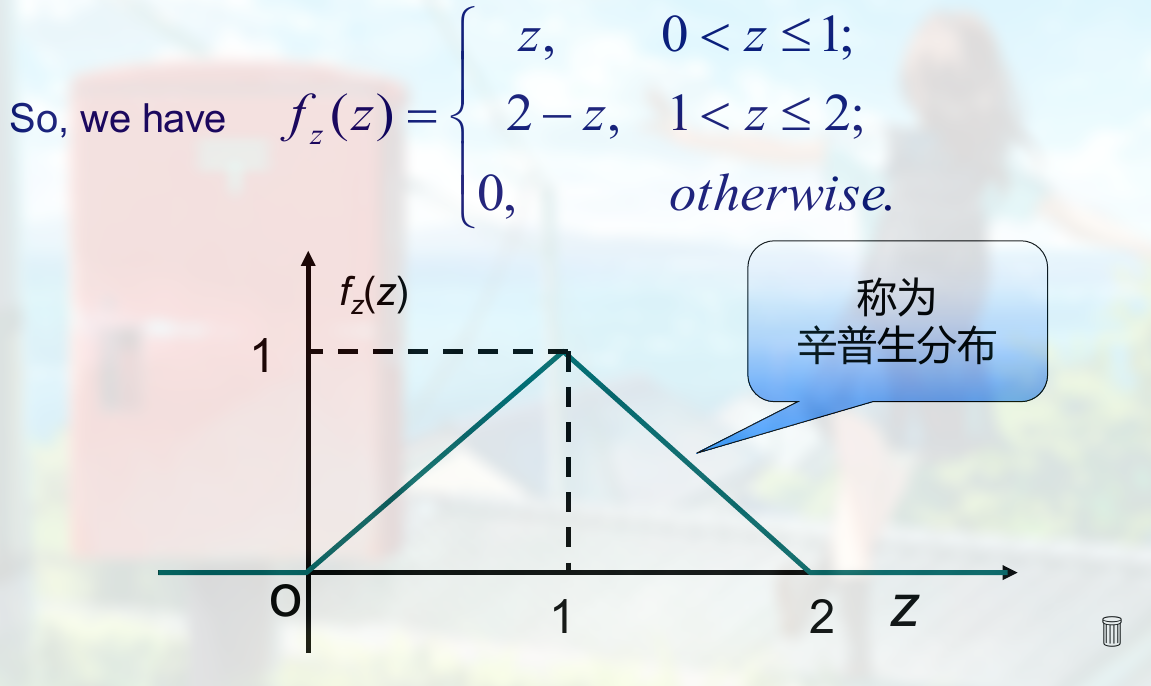
重要的是通过题意来得到 $x,z$ 的范围和线性式.

做题步骤:

1. 写出概率密度表达式
2. 写出 domain G, 进而写出 x 和 z 的范围
3. 画出 x-z 坐标图
4. 根据 z 的范围分别积分

正态分布

一般来说, $\phi$ 来表示其密度函数(小写), $\Phi$ 来表示分布函数 (大写).

正态分布的密度函数:

$$
\displaylines
{
\phi(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{ - \frac{(x-\mu)^2}{2 \sigma^2} } \newline~ \newline
-\infty < x < +\infty
}
$$
表示为 $X \sim N(\mu, \sigma^2)$

其图像大概为:

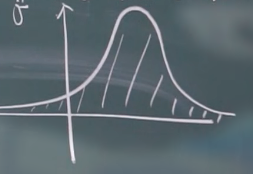
一个积分的结论:

$$
\displaylines
{
\int_{-\infty}^{+\infty} e^{-x^2}dx = \sqrt{\pi}
}
$$

这个密度函数的积分结果为 1 (过程就不写了):

$$
\displaylines
{
\int_{-\infty}^{+\infty} \phi(x)dx
}
$$
( $\phi(x)$ 中的 $\sqrt{2\pi}$ 就是为了将积分结果配为 1 而加上去的 )

分布函数:

$$
\displaylines
{
\Phi(x) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^{x} e^{- \frac{(t-\mu)^2}{2 \sigma^2}} dt
}
$$
( $\int e^{-x^2}dx$ 除了上面那个结论外, 积不出来 )

结论:

• $y = \phi(x)$ 以 $x = \mu$ 为对称轴.
• $x = \mu$ 时, $\phi(x)$ 的最大值为 $\frac{1}{\sqrt{2\pi} \sigma}$
• $\sigma$ 固定, $\mu$ 改变, 图像左右移动
• $\mu$ 固定, $\sigma$ 变化, $\sigma$ 变小, 最高点上移 (但面积不变)

画图技巧:

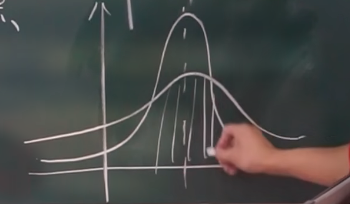
做题时一般都会转化为 标准正态分布 , 即 $\mu = 0$, $\sigma = 1$. 即:

$$
\displaylines
{
\phi_0(x) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}},\ \ -\infty < x < +\infty \newline~ \newline
\Phi_0(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{- \frac{t^2}{2}} dt
}
$$

其图像大概为:

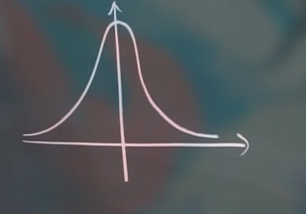
性质:

• $\Phi_0(x) = \Phi_0 (-x)$ 和 $\Phi_0(-x) = 1 - \Phi_0(x)$

查表:

• $x \ge 5,\ \ \phi_0(x) = 0, \ \ \Phi_0(x) = 1$
• $x \ge -5,\ \ \phi_0(x) = 0, \ \ \Phi_0(x) = 1$

等.

将一般的正态分布化为标准正态分布

密度函数的转化
$$
\displaylines
{
\phi(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{ - \frac{(x-\mu)^2}{2 \sigma^2} } \newline~ \newline
-\infty < x < +\infty \newline~ \newline
将 ( \frac{x-\mu}{\sigma} ) 看作一个变量, 得: \newline~ \newline
\phi(x) = \frac{1}{\sigma}[ \frac{1}{\sqrt{2\pi}} e^{- \frac{( \frac{x-\mu}{\sigma} )^2}{2}}] \newline~ \newline
( 后者是标准正态分布的形式了 ) \newline~ \newline
= \frac{1}{\sigma} \phi_0( \frac{x-\mu}{\sigma} )
}
$$

分布函数的转化:

同样吧 $\sigma^2$ 从分母移到分子, 构成一个参数:

$$
\displaylines
{
\Phi(x) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^{x} e^{- \frac{(t-\mu)^2}{2 \sigma^2}} dt \newline~ \newline
\Phi(x) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^{x} e^{- \frac{( \frac{t-\mu}{\sigma} )^2}{2 }} dt \newline~ \newline
(对微分做个调整, 加一个 -\mu 以及将 \frac{1}{\sigma} 移过来) \newline~ \newline
= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{- \frac{( \frac{t-\mu}{\sigma} )^2}{2 }} d( \frac{t - \mu}{\sigma} ) \newline~ \newline
因此: \newline~ \newline
\Phi(x) = \Phi_0( \frac{x- \mu}{\sigma} )
}
$$
不是标准的一般都要化成标准的.

概率的计算:
$$
\displaylines
{
P\{ 0<x<1.6\} = \Phi(1.6) - \Phi(0) \newline~ \newline
= \Phi_0( \frac{1,6 - \mu}{\sigma} ) - \Phi_0( \frac{0-\mu}{\sigma} )
}
$$

也可以直接在范围里转换成标准正态分布:

$$
\displaylines
{
P\{ \left\vert X \right\vert \le 2\} = P \{-2 \le x \le 2 \} = P \{ \frac{-2 - \mu}{\sigma} \le \frac{x-\mu}{\sigma} \le \frac{2-\mu}{\sigma} \} \newline~ \newline
(此时已经是标准正态分布了)
}
$$

$3\sigma$ 准则.

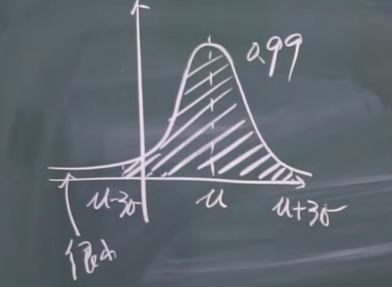
上 $\alpha$ 分位数, 即 $\mu_{\alpha}$ , 如:
$$
\displaylines
{
\mu_{0.05} = 1.645 \newline~ \newline
等价于: P \{X > 1.645 \} = 0.05
}
$$
(上, 指的就是右侧的面积, $\alpha$ 就是面积, 也就是概率)

期望

对于不连续的数来说:

$$
\displaylines
{
E(X) = \sum_{All\ x} xf(x)
}
$$

对于连续的数来说:

$$
\displaylines
{
E(X) = \int xf(x) dx
}
$$

伯努利试验的期望为 $p$

n 重伯努利试验的期望为 $np$

其他几个重要分布的期望的推导.

一个期望不存在的例子:

为何下列期望为无限:

正态分布的期望为 $\mu$

期望的一个性质: if there exists a constant such that $Pr(X \ge a)$, then $E(X) \ge a$. If there exists a constant b such that $Pr(X \le b) = 1$ then $E(X) \le b$

还有:

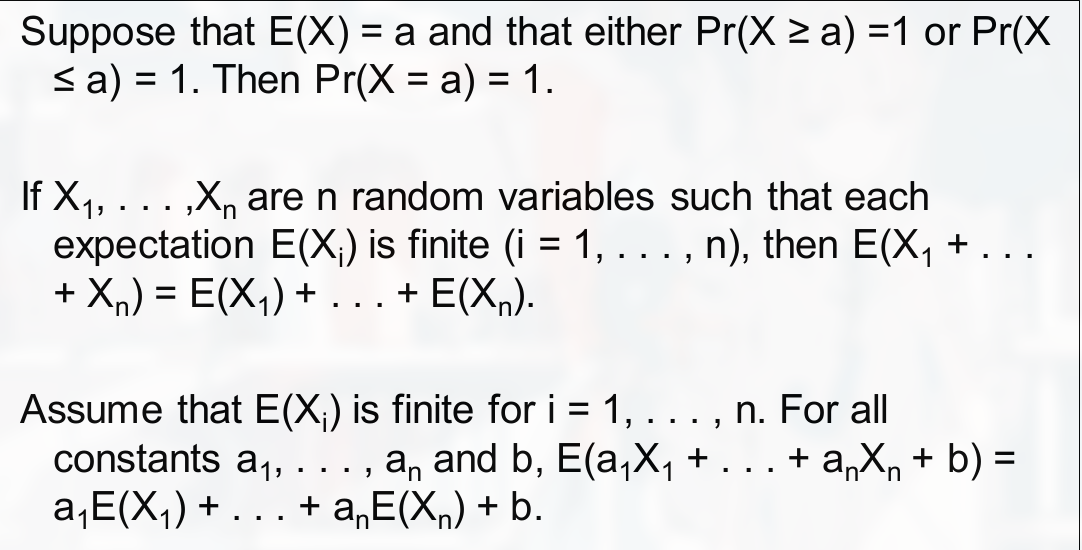
独立变量的期望

注意 mean 和 median 的区别 (平均数和中位数)

Mean $\rightarrow$ Expectation

Median $\rightarrow$ m, $X:Pr(X \le m) \ge 1/2\ and\ Pr(X \ge m) \ge 1/2$

中位数的一个示例:

One-to-One Function 指一对一函数, 作用是啥不清楚.

条件期望 Conditional Expectation

离散, 如:
$$
\displaylines
{
E(Y|x) = \sum_{ALL\ y} y g_2(y|x)
}
$$

连续, 如:

$$
\displaylines
{
E(Y|x) = \int_{-\infty}^{+\infty} y g_2(y|x)dy
}
$$

方差

$$
\displaylines
{
\mu = E(X) \newline~ \newline
Var(X) = E[(X-\mu)^2]
}
$$

方差的简便计算:
$$
\displaylines
{
Var(X) = E(X^2) - [E(X)]^2
}
$$

正态分布的方差为:

$$
\displaylines
{
Var(X) = \sigma^2
}
$$

将正态分布转化为标准形式:

样本平均值 (Sample Mean) 指:

$$
\displaylines
{
\frac{1}{n} \sum_{i=1}^n X_i
}
$$

常常写作 $\overline{X_n}$

Cauchy Distribution 指柯西分布. 其均值和方差都不存在.

四分位间距 (Interquartile Range):

$$
\displaylines
{
F^{-1} (p)\ for\ 0<p<1 \newline~ \newline
此时, 四分位间距为: \newline~ \newline
F^{-1}(0.75) - F^{-1}(0.25)
}
$$

不会积分的题:

矩 Moments

随机变量的幂的期望, 即 $X^k\ for\ k>2$ 的期望, 有重要的理论性质.

$E(X^k)$ 被称为 kth moment of X.

一个性质:

中心矩 (Central Moments) , 若 $E(X) = \mu$, 那么 $E[(X-\mu)^k]$ 被称为 the kth central moment of X or the kth moment of X about the mean

矩生成函数 (Moment Generating Function) , $X$ 为随机变量, $t$ 为实数, 定义:

$$
\displaylines
{
\psi(t) = E(e^{tX})
}
$$
这个 $\psi(t)$ 就称为 the moment generating function. (简写为 m.g.f.)

一个性质:

X 是一个随机变量, 如果 $m.g.f.$ 对于 all values of t in some open interval around point $t=0$有限, 那么有:

$$
\displaylines
{
E(X^n) = \psi^{(n)}(0),\ \ n=1,2,…
}
$$
(后者指 n 阶导)

这个式子可以方便矩,方差和期望的计算

$$
\displaylines
{
E(X) = \psi’(0) \newline~ \newline
E(X^2) = \psi’’(0) = 2 \newline~ \newline
Var(X) = \psi’’(0) - [\psi’(0)]^2
}
$$

注意 各个分布的 m.g.f. 的计算.

协方差和相关性 Covariance and Correlation

协方差是衡量两个随机变量之间的线性关系的一种统计量。它表示两个变量的变化趋势是否一致。如果两个变量的变化趋势一致，那么它们之间的协方差就是正值；如果两个变量的变化趋势相反，那么它们之间的协方差就是负值；如果两个变量之间没有相关性，那么它们之间的协方差就是0。

$$
\displaylines
{
E(X) = \mu_X,\ \ E(Y) = \mu_Y \newline~ \newline
Cov(X,Y) = E[(X-\mu_X)(Y-\mu_Y)]
}
$$

感觉和方差类似, 毕竟 $Var(X) = E[(X-\mu)^2]$, 这里就相当于将一个 $(X-\mu)$ 换成了 $(Y-\mu_Y)$

协方差的简便算法, 如果对于所有随机变量 $X$ 和 $Y$ 有 $\sigma_X^2 < \infty$ 以及 $\sigma_Y^2 < \infty$, 则有:
$$
\displaylines
{
Cov(X,Y) = E(XY) - E(X)E(Y)
}
$$

相关性

X 和 Y 是随机变量且有有限的 variances $\sigma_X^2$ 和 $\sigma_Y^2$, 因此 X 和 Y 的 correlation 记为 $\rho (X,Y)$:
$$
\displaylines
{
\rho(X,Y) = \frac{Cov(X,Y)}{\sigma_X \sigma_Y}
}
$$

施瓦兹不等式 (Schwarz Inequality) , 对于所有随机变量 $U$ 和 $V$, 有：

$$
\displaylines
{
[E(UV)]^2 \le E(U^2)E(V^2)
}
$$
如果方程右边有限, 那么相等条件为非零常数:

$$
\displaylines
{
aU + bV = 0
}
$$
(U 与 V 成线性比例)

柯西-施瓦兹不等式 (Cauchy-Schwarz Inequality)

$$
\displaylines
{
[Cov(X,Y)]^2 \le \sigma_X^2 \sigma_Y^2 \newline~ \newline
and \newline~ \newline
-1 \le \rho (X,Y) \le 1
}
$$
相等条件为, 非零常数:

$$
\displaylines
{
aX + bY = c
}
$$

正相关 (positively correlated) 指 $\rho(X,Y) > 0$

负相关 (negatively correlated) 指 $\rho(X,Y) < 0$

如果 $\rho (X,Y) = 0$ 则是不相关 (uncorrelated)

协方差和相关性的性质:

• X, Y 独立, 则 $Cov(X,Y) = \rho(X,Y) = 0$

线性相关时:

大量随机样本

这一章说明样本均值与构成样本的各个随机变量的期望之间的联系.

对于大量随机样本, 不太可能精确地计算 sample average 的概率是靠近 $0.5$ 的.

大数定律 (The law of large numbers), 在数量很大时可以用下列的不等关系.

马尔可夫不等式 (Markov Inequality) , $Pr(X \ge 0) = 1$, t 是实数且 $t > 0$:

$$
\displaylines
{
Pr(X \ge t) \le \frac{E(X)}{t}
}
$$
( 可以看出, 这是期望和总概率之间的联系, 证明过程 PPT 有, 这里暂时不了解 )

切比雪夫不等式 (Chebyshev Inequality) , $Var(X)$ 存在, 对于任意 $t > 0$:

$$
\displaylines
{
Pr( \left\vert X - E(X) \right\vert \ge t) \le \frac{Var(X)}{t^2}
}
$$
(可以看出是概率和方差的关系, 其由马尔可夫不等式得来, 当 $Y = X - E(X)$ 时可转化得到)

一个分布的简单随机样本 (simple random sample of a distribution) , X with a given distribution, 序列 $\{X_i\}$ 中每个元素每选中的概率相同.

样本均值 (sample mean) :
$$
\displaylines
{
\overline{X_n} = \frac{1}{n}(X_1 + … + X_n)
}
$$

样本若来自一个 distribution with mean $\mu$ and variance $\sigma^2$, 则 $\overline{X_n}$ 的 mean 和 variance 为:
$$
\displaylines
{
E(\overline{X_n}) = \mu \newline~ \newline
Var(\overline{X_n}) = \frac{\sigma^2}{n}
}
$$

一个切比雪夫不等式的例题:

注意观察题目中, 出现了 mean $\mu$, variance $\sigma$, 总数 $n$ 这些关键信息.

另一道例题:

需要注意, 解这类题, 由于需要的是期望和方差, 因此需要先判断 sample 是来自那一个 distribution, 进而能够得到. 由于这里是二项分布 (binomial distribution), 因此可以得到 $E(X) = \frac{n}{2}$, 以及 $Var(T) = \frac{n}{4}$

合理利用不等式的 $\le$ 和 $\ge$

变换为绝对值形式:

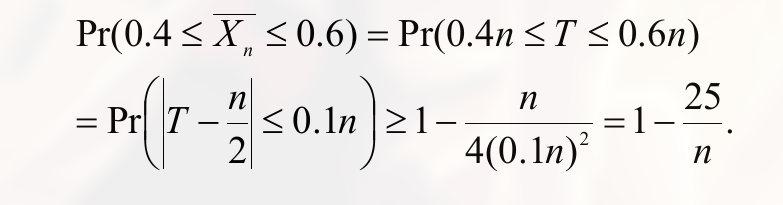
概率收敛 (Convergence in Probability)

$Z_n$ converges to $b$ in probability:

$$
\displaylines
{
Z_n \overset{a}{\rightarrow} b
}
$$

即:

$$
\displaylines
{
\lim_{n \rightarrow \infty} Pr( \left\vert Z_n - b \right\vert < \epsilon ) = 1
}
$$

弱大数定理 (Weak law of large numbers)

(也就是收敛于 期望 )

强大数定理 (the strong law of large numbers)

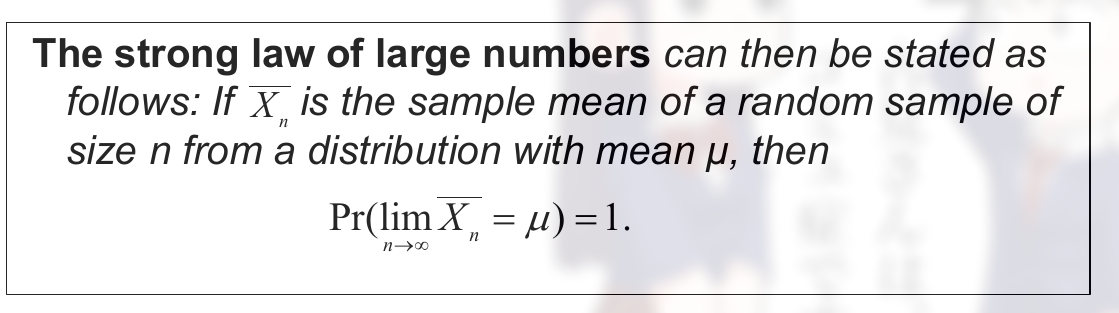
这一章的定理和例题没怎么看.

中心极限定理

如果一个随机现象是由大量的, 相互独立的因素所影响的, 如大炮射击, 受温度, 湿度, 材料… 这里的因素必须是大量的, 独立的, 且这些因素每一个起的作用都不是特别大.

(当题中出现, 将所有样本相加时就可以想到这个定理)

定义: 大量, 独立, 同分布的随机变量(也就是因素)之和的极限分布是正态分布.

对中心极限定理的名字的解释,中心 两个字无实质意义, 极限 就是指上述提到的和的极限.

定理: $x_1,…,x_n$ 独立同分布 (不管什么分布), $E(x_i) = \mu,\ Var(x_i) = \sigma^2,\ \ 0< \sigma^2 < +\infty$, 则有:

$$
\displaylines
{
\lim_{n \rightarrow \infty} P( \frac{\sum_{i=1}^n x_i - n \mu}{\sqrt{n} \sigma} \le X) = \Phi_0(x)
}
$$
( $\sum_{i=1}^n x_i$ 代表所有量的和, $\Phi_0(x)$ 指标准正态分布 )

若:
$$
\displaylines
{
Y = \sum_{i=1}^n x_i \newline~ \newline
\therefore E(Y) = E(\sum_{i=1}^n x_i) = n \mu \newline~ \newline
(毕竟都独立, 可以都提出来相加) \newline~ \newline
Var(Y) = Var(\sum_{i=1}^n x_i) = \sum_{i=1}^n Var(x_i) = n \sigma^2
}
$$

这里相当于就是标准化的过程, 将一般的正态分布化为标准的正态分布为:

$$
\displaylines
{
\phi(x) = \phi_0( \frac{x - \mu}{\sigma} )
}
$$

而这里则将:

$$
\displaylines
{
\frac{x - \mu}{\sigma} \rightarrow \frac{\sum_{i=1}^n x_i - n \mu}{\sqrt{n} \sigma}
}
$$

因此有:
$$
\displaylines
{
将: \newline~ \newline
\frac{\sum_{i=1}^n x_i - n \mu}{\sqrt{n} \sigma} 视为标准正态分布 \rightarrow N(0,1) \newline~ \newline
将: \newline~ \newline
\sum_{i=1}^n x_i 视为一般正态分布 \rightarrow N(n\mu,n\sigma^2)
}
$$

使用例题:

中心极限定理的特例 – 棣莫弗–拉普拉斯中心极限定理, $Y_n$ 是参数为 $n,p$ 的二项分布, 则有:

$$
\displaylines
{
\lim_{n \rightarrow \infty} P( \frac{Y_n - nP}{\sqrt{np(1-p)}} \le x ) = \Phi_0(x)
}
$$
($Y_n$ 指发生的次数)

$Y_n$ 和 $\sum_{i=1}^n x_i$ 的关系:
$$
\displaylines
{
Y_n = \sum_{i=1}^n x_i, \ \ x_i = \begin{cases}
1,\ \ 发生 \newline~ \newline
0,\ \ 未发生
\end{cases}
}
$$

因此:

$$
\displaylines
{
E(x_i) = p \newline~ \newline
Var(x_i) = p(1-p)
}
$$

这个特例就是用正态分布来近似二项分布.

参数估计

7.1 点估计 , 区间估计

总体分布	总体的参数
$N(\mu,\sigma^2)$	$\mu,\sigma^2$
$p(\lambda)$	$\lambda$
$[a,b]$	$a,b$

然后通过取一些样本, 来估计这些参数.

参数空间, 就是参数的取值范围.

点估计 , 就是用一个数来估计. 如 $185$

区间估计 , 取一个区间来估计. 如 $182 \sim 188$

估计的写法为:
$$
\displaylines
{
\hat{\theta} = \hat{\theta}(x_1,…,x_n)
}
$$
(前者是我们要估计的参数, 后者是用取得样本构造的函数, 带 $\hat{ }$ 的原因是表示估计值 )

矩估计法

思想为, 用样本的矩代替总体的矩:

$$
\displaylines
{
总体的矩 \leftarrow 样本的矩 \newline~ \newline
一阶 E(X) \leftarrow 一阶 \overline{x} = \frac{1}{n} \sum x_i \newline~ \newline
二阶 E(X^2) \leftarrow 二阶 A_2 = \frac{1}{n} \sum (x_i-\mu)^2
}
$$

例题:

一阶矩用来求期望, 二阶矩用来求方差.

泊松分布的期望和方差都为 $\lambda$

两个参数, 矩估计就需要两阶.

均匀分布的期望就是其中点 $\frac{a+b}{2}$

极大似然估计法

古典概型中, 参数是已知的, 而这里的总体是未知的:

概率大的事件比概率小的事件更容易发生.

将, 使事件 A 发生的概率, 最大, 的参数值做为估计值.

(极大, 就是最大, 似然, 就是可能性)

解题步骤:

1. 写出概率/密度函数 (离散或连续型)
2. 写似然函数 $L(\theta)$ (这里的参数会变), 似然函数都是连乘
3. 两边取 $\ln$
4. 两边对参数求导, 令导数等于 0

样本都是确定数, 求导时会为 0.

示例:

泊松分布的 $\lambda$ 估计出来就是样本均值.

抽样

抽样: 从总体中抽取一部分. 取 n 次的样本变量 $(X_1,…,X_n)$, 样本观测值 $(x_1,…,x_n)$ (具体值)

注意 统计量的定义 , 不含任何未知参数的样本的函数. (用样本构造一个函数), 如:

是统计量的例子:
$$
\displaylines
{
x_1 + x_2 + … + x_n\ (直接将样本相加, 不含未知参数) \newline~ \newline
x_1^2 + … + x_n^2 \newline~ \newline
max{ \left\vert x_1 \right\vert … \left\vert x_n \right\vert }
}
$$

不是统计量的例子:
$$
\displaylines
{
若题中明确给出 \mu 未知,\ 则(x - \mu)^2 + … + (x_n - \mu)^2
}
$$

常见统计量有:

抽样分布

统计量的分布就称为抽样分布.

几个分布:

1. 正态分布
2. $X^2$ 分布 (不用看密度函数)

对于 $X^2$ 分布, 有 $X^2(n)$ 这里的 n 为自由度, 注意自由度不同时的图像:

1. $X^2(2)$ , 此时为 $\lambda = \frac{1}{2}$ 的指数分布
2. $n \ge 3$, 为单峰曲线, 在 $n-2$ 时取最大, 且 n 增大时, 峰向右, 且越来越对称, 当 n 很大时, 可用正态分布来近似.
   (上面这些用处不大)

一个定理: $x_1,…x_n$ 独立, 且属于标准正态分布, 此时 $\sum_{i=1}^n x_i^2 \sim X^2(n)$, 也就是此时分布求和就是自由度为 n 的 $X^2$ 分布. (可以看出, 自由度取决于样本数量)

$X^2$ 分布的 $E(X) = n, Var(X)=2n$

有中心极限定理可知, 若 x 是 $X^2$ 分布 (即 X \sim X^2(n)), 当 n 充分大时, 有: $\frac{x-n}{\sqrt{2n}} \overset{近似}{\sim} N(0,1)$

两个 $X^2$ 分布相加, 结果也是 $X^2$ 分布, 并且自由度为原来自由度相加, 即 $X \sim X^2(n),\ Y \sim X^2(m),\ \ X,Y独立, \ X+Y \sim X^2(m+n)$

上 $\alpha$ 分位数:

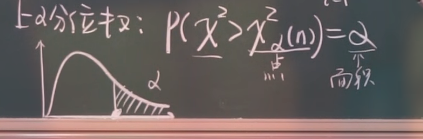
如: $X^2_{0.05}(10)=18.3$, 这里, 平方表明满足的是 $X^2$ 分布, $(10)$ 表示的是自由度. $18,3$ 表示点. 这个点右边的概率就是 $0.05$

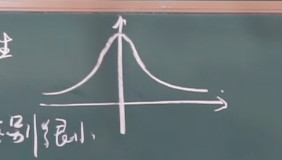
t 分布 (名字没什么意义, 只是因为作者用 student 发表的), 其和正态分布比较相似 (不用记忆密度函数)

图像为:

$$
\displaylines
{
X \sim t(n)
}
$$
这里同样有自由度的概念, $n$ 的值越大, 其和正态分布越相似. ( $n \ge 30$ 时区别很小 )

定理: 若 $X \sim N(0,1),\ Y \sim X^2(n)$, 且 X, Y 独立, 那么 $\frac{x}{\sqrt{Y/n}} \sim t(n)$ (也就是说, 一个标准正态分布和一个 $X^2$ 分布可以构造一个 t 分布), 这里 $X^2$ 分布的自由度为多少, $t$ 分布的自由度就为多少.

参数估计的例题

注意矩估计量和矩估计值的写法, 一个为大写, 表示变量, 一个是小写, 表示观测值:

矩估计法, 的结果中, 包含期望和方差, 也就是用期望和方差来估计.

求最大似然估计值和估计量

似然函数的写法, 是累乘:

步骤:

1. 写出似然函数
2. 取对数 $\ln$
3. 对未知参数求导, 并取导数为零
4. 化简

同样注意最大似然估计值和最大似然估计量的区别.

习题册做到第 4 题了.

假设检验

三个结论:

第一个结论

如果
$$
\displaylines
{
\overline{X} \sim N(\mu, \frac{\sigma^2}{n})
}
$$
(如果一个量满足这个式子)
那么:
$$
\displaylines
{
\frac{\overline{X} - \mu}{\sigma / \sqrt{n}} \sim N(0,1)
}
$$
(其标准化的写法)

第二个结论

如果:
$$
\displaylines
{
\frac{(n-1)s^2}{\sigma^2} \sim X^2 (n-1)
}
$$
(前面的形式服从卡方分布, $s$ 表明未知的 $\sigma$, 已知的为抽样测出来的)

第三个结论

$$
\displaylines
{
\frac{\overline{x} - \mu}{s/\sqrt{n}} \sim t(n-1)
}
$$
(这个形式则服从 t 分布)

t 分布和标准正态分布的区别就是将 $\sigma$ 换成了 $s$.

置信水平

两个概念:

• $\alpha$: 表明稀有事件发生的概率. (似乎也就是拒绝域)
• $1-\alpha$: 表明大概率事件

设置信水平为 $1-\alpha$ 就是 把事件限制在大概率范围内

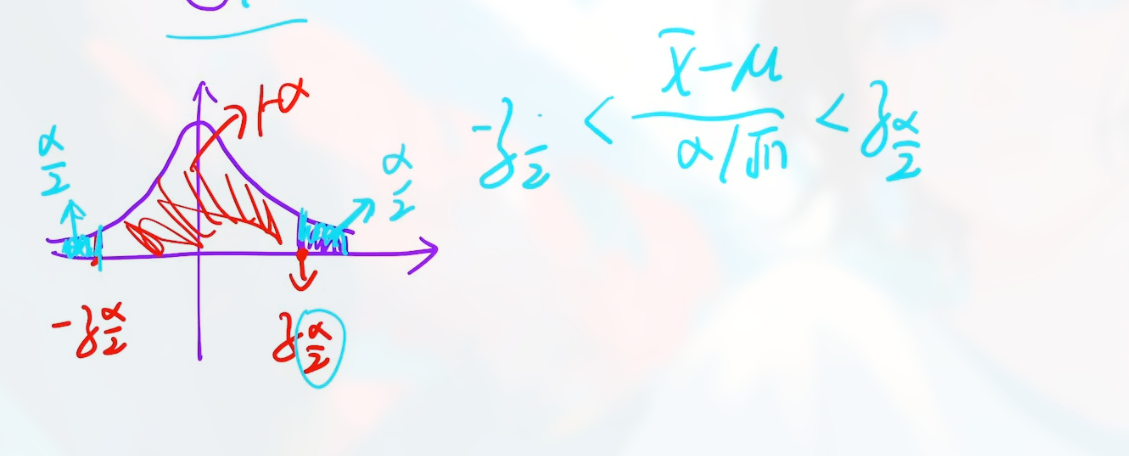
这里要用到 上 $\alpha$ 分位数 , 此时两侧的概率相加就是 $\alpha$.

求置信区间似乎就是求某个参数的范围.

哪一个未知就不能用哪一个.

题型 1 如题干中说了 $\mu$ 未知, 求 $\mu$ 的置信区间

解题就如:

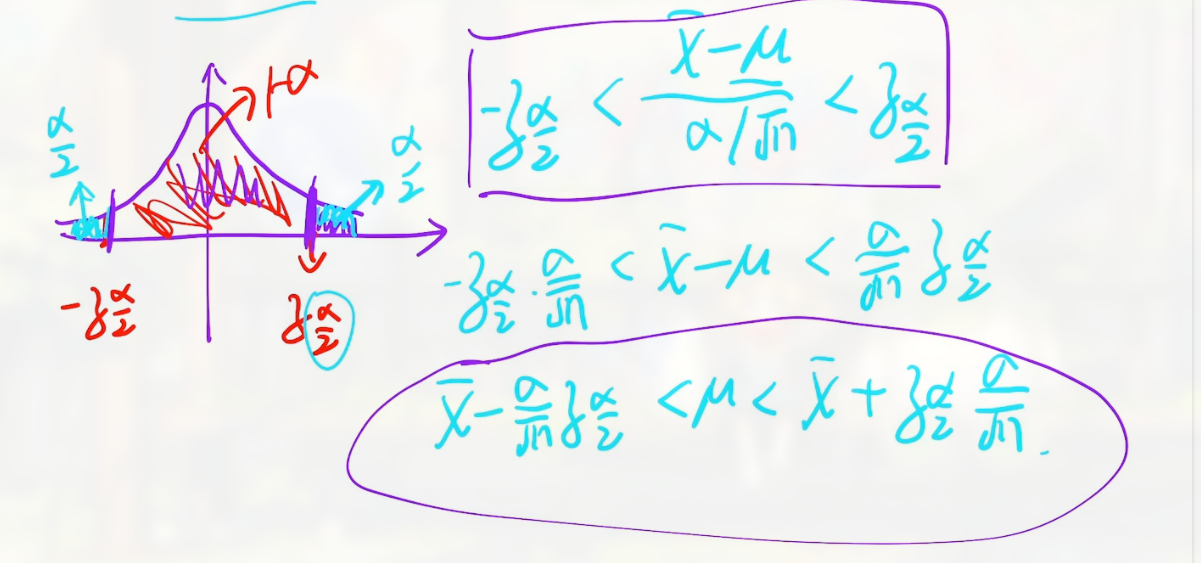
题型 2 , 题干说 $\sigma$ 未知, 那么默认会有 $s$ 已知, 求 $\mu$ 的置信区间

给出的 $t_{ \frac{\alpha}{2}}(n-1)$ 就是一个点

同样是利用 上 $\alpha$ 分位数 的概念.

解题如:

题型 3, $\mu$ 未知, $\sigma$ 未知, 求 $\sigma^2$ 的 $1-\alpha$ 置信区间

假设检验做题

做完题后要给出结论.

步骤:

1. 下假设结论
2. 计算统计量
3. 计算拒绝域
4. 比较, 下结论

假设检验就是把假设带进去.

假设检验步骤

假设检验包括:

1. 参数假设检验

如: 已知 $X \sim N(\mu, \sigma^2)$, $\mu,\sigma$ 未知. 假设 $\mu = \mu_0$, 利用给出的样本 $x_1,…,x_n$ 来判断, $\mu$ 是否真的等于 $\mu_0$ (即假设是否成立)

2. 非参数假设检验

如: 分布未知

几个概念:

1. 原假设, $H_0: \mu = \mu_0$ (概率比较大)
2. 被择假设, $H_1: \mu \ne \mu_0$

若我们得到 $\mu \ne \mu_0$, 则假设是错误的, 此时取的样本就属于拒绝域 $x_1,…,x_n \in K_0$, 称为拒绝原假设.

成立的话称为 接受原假设 .

在拒绝域中的样本, 才能判断假设不成立.

若样本不在拒绝域中, 那么可以判断假设成立.

will you incline to which of the above two choices? 的意思是, 你会倾向于…

罕见事件原理 (the principle of rare event) 表明, a rare event will not occur in a single observation.

有两个参数空间 (也就是参数可能的范围):

• $\Omega_0$
• $\Omega_1$

且:
$$
\displaylines
{
在 H_0 中:\ \theta \in \Omega_0 \newline~ \newline
在 H_1 中:\ \theta \in \Omega_1 \newline~ \newline
\Omega_0 \sqcap \Omega_1(两者 disjoint) \newline~ \newline
\Omega_0 \cup \Omega_1 = \Omega
}
$$

像这样的一个问题, 哪一个猜测是正确的, 这种问题就称为假设检验 (a problem of testing hypotheses)

决定哪一个是正确的的过程称为测试步骤 (test procedure)

如果我们认为 $\theta$ 在 $\Omega_1$ 中, 则称为 reject $H_0$

如果认为在 $\Omega_0$ 中, 则称为 not to reject $H_0$

$\theta$ 似乎都写为向量的形式, 如两个参数未知, 写成: $\theta = (\mu, \sigma^2)$.

简单和复合假设 (simple and composite hypotheses)

• 如果 $\Omega_i$ 中包含一个值, 那么就是简单假设
• 如果 $\Omega_i$ 中包含多个值, 那么就是复合假设

如, 一个简单假设可能为: $H_0: \theta = \theta_0$

单边假设和双边假设 (one-sided and two-sided hypotheses)

• 单边假设如: $H_0: \theta \le \theta_0,\ \ H_1: \theta > \theta_0$
• 双边假设如: $H_1: \theta \ne \theta_0$

临界区和测试统计 (the critical region and test statistics)

• 临界区, 常常写为 $T = r(X)$ (似乎和拒绝域作用相同)
• 如果有 reject $H_0$ if $T \in R$, 则称 T 是一个 test statistic, $R$ 是这个测试的拒绝域 (rejection region)

幂函数和错误类型 (The Power Function and Types of Error)
若 $\delta$ 为 test procedure, 那么 $\pi (\theta|\delta)$ 则为 power function of the test $\delta$, 如果 $S_1$ 表示 $\delta$ 的 critical region, 那么有:

$$
\displaylines
{
\pi (\theta|\delta) = Pr(X \in S_1|\theta)\ \ for\ \ \theta \in \Omega
}
$$

如果 $\delta$ 是一个 test statistic T, 且拒绝域为 $R$, 那么有:

$$
\displaylines
{
\pi (\theta|\delta) = Pr(T \in R|\theta)\ \ for \ \ \theta \in \Omega
}
$$

有两类错误:

• 弃真错误 , 当 $H_0$ 成立, 但拒绝 $H_0$ 时
• 取伪错误, 当 $H_0$ 不成立, 但接受 $H_0$ 时

显著性 ( $\alpha$ ) 水平

显著水平，也称为α水平或显著性水平，是用于衡量在假设检验中拒绝原假设的临界值。通常情况下，显著水平的取值为0.05或0.01，代表了在一次实验中，我们允许犯错误的概率大小。

p-值

一般的，p值是最小的显著性水平$\alpha_0$

假设检验的步骤

1. 确定原假设和备择假设：原假设（null hypothesis）是我们想要检验的陈述，通常是指样本数据与总体相同。备择假设（alternative hypothesis）则是与原假设相反的假设，通常是指样本数据与总体不同。

2. 确定显著水平：显著水平（significance level）是判断是否拒绝原假设的临界值，通常设定为0.05或0.01。

3. 选择合适的假设检验方法：根据样本数据类型和实验设计等因素，选择合适的假设检验方法，如t检验、F检验、卡方检验等。

4. 计算统计量：根据假设检验方法的要求，计算相应的统计量，如t值、F值、卡方值等。

5. 确定拒绝域：拒绝域是指统计量达到或超过一定临界值时，我们会拒绝原假设的范围。

6. 计算p值：p值是指在原假设成立的情况下，出现观察值或更极端观察值的概率。通过计算p值，我们可以判断观察值是否落在了拒绝域内。

7. 做出结论：根据p值或统计量是否达到拒绝域，来判断是否拒绝原假设。如果拒绝原假设，则说明样本数据与总体存在显著差异；反之，则说明样本数据与总体相同。

t 检验适用的情况

t检验适用于总体标准差未知或样本容量较小的情况，或者总体分布近似正态分布的情况.

t 统计量的计算式:

假设检验习题

概念, 显著水平, 什么时候采用 t 检验.

可能的考试重点

• 全概率公式, 贝叶斯公式
• 中心极限定理
• 大数定理结论
• 标准正态分布
• 各分布的结论
• 方差, 标准差, 期望
• 假设检验一定有一道大题
• 指数分布无记忆
• 均匀分布
• 标准分布的标准化

往年卷

第一题

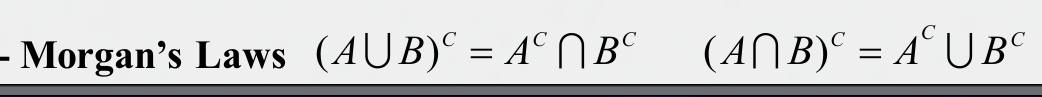
泊松分布平方的期望为原期望的平方.

求 quantile function 就是把 x 表示成 p 的表达式.