Digital-Logic-Design-and-Application-课程笔记
Lecturer: 卢有亮
Number: 19934306528
需安装的工具: Vivado
课程构成:
- foundation of digital system
- analysis and design a digital circuit
- CPU tech
- use HDL to design a simple CPU
Topic1 Introduction
数字信号很抗干扰.
数的位置多项式表示法, 如:
$$
\displaylines
{
N = 251.41_{10} \ \ \ Decimal \newline~ \newline
N = 1100.11_{2} \ \ \ Binary\newline~ \newline
N = 127.4_{8} \ \ \ Octal\newline~ \newline
N = B65F_{16} \ \ \ Hexadecimal\newline~ \newline
}
$$
尾缀表示 base, 基数.
以十进制和二进制的举例:
$$
\displaylines
{
N = 251.41_{10} = 2 \times 10^{2} + 5 \times 10^{1} + 1 \times 10^{0} + 4 \times 10^{-1} + 1 \times 10^{-2} \newline~ \newline
N = 251.41_{2} = 2 \times 2^{2} + 5 \times 2^{1} + 1 \times 2^{0} + 4 \times 2^{-1} + 1 \times 2^{-2} \newline~ \newline
}
$$
(八进制和十六进制同理)
一个十进制转二进制的示例:
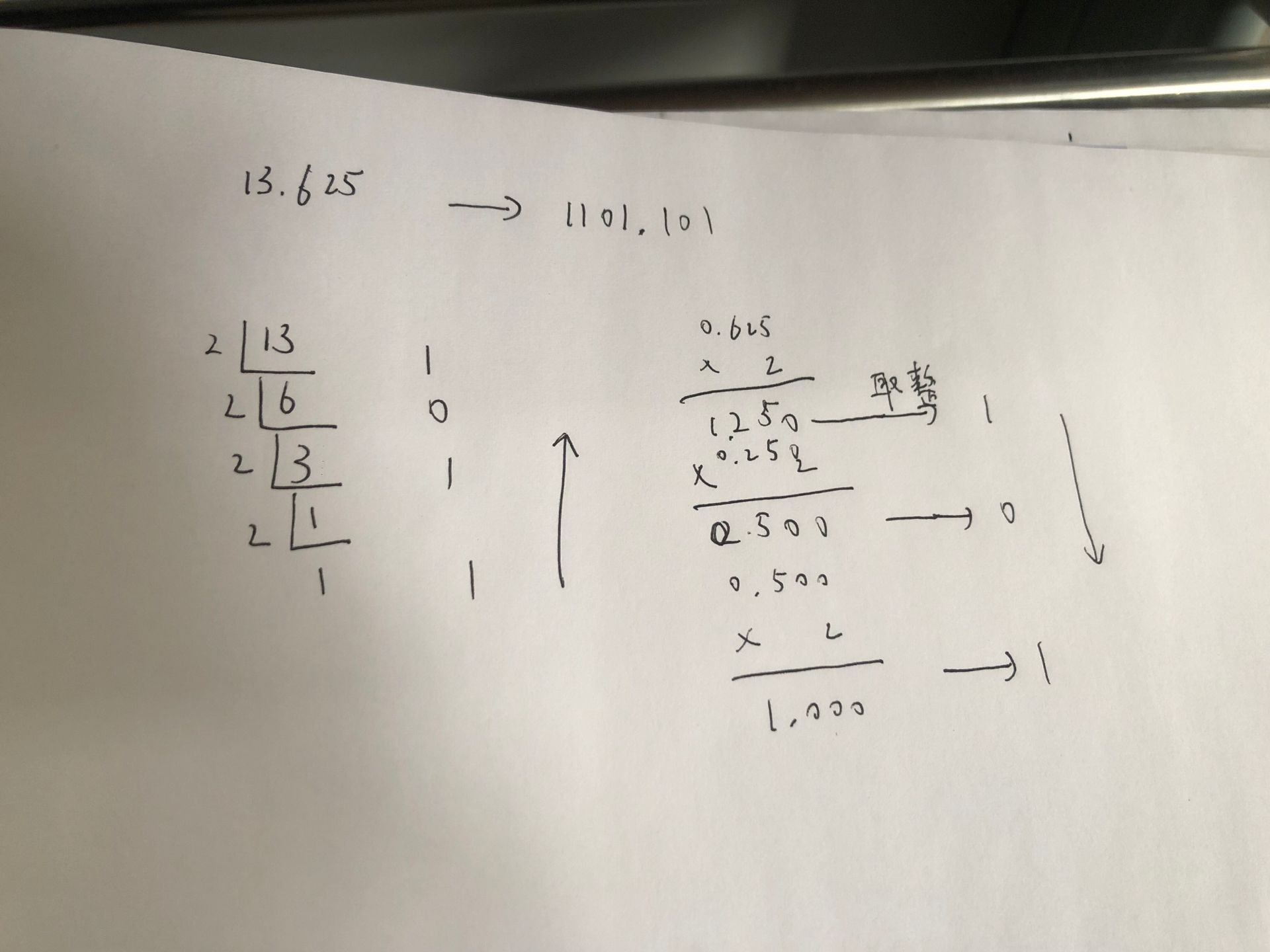
八进制和十六进制转二进制都可以直接拆开, 不管是整数部分还是小数部分, 一个八进制对应三个二进制数, 一个十六进制数对应四个二进制数, 如:


按位计数制 Positional Number Systems
即, 按每个数码的位置规定其所具有的数值, 如:
$$
\displaylines
{
1985_{10} = 1 \times 10^3 + 9 \times 10^{2} + 8 \times 10^1 + 5 \times 10^0 \newline~ \newline
= 1000 + 900 + 80 + 5
}
$$
这里的 10 称为 记数制的基数
MSB (Most Significant Bit), 指最高有效位.
LSD (Least Significant Bit), 指最高有效位.
如果有 n 位二进制位, 那么其表示的范围为:
$$
\displaylines
{
0 \sim 2^n -1
}
$$
如, 有 10 个二进制位, 则其能表示的范围为:
$$
\displaylines
{
0 \sim 2^10 - 1
}
$$
推导:
$$
\displaylines
{
最小数: 0000000000 = 0 \newline~ \newline
最大数: 1111111111 = 2^9 + 2^8 + … + 2^0 \newline~ \newline
= 2^{10} - 1
}
$$
一个和精度相关的例题:

符号表示
最高位用来表示正负:
- 最高位为 0 表示正 (+)
- 最高位为 1 表示负 (-)
如:

原码, 补码和反码.
原码
如:

表示的就是原码.
反码 1’s complement
原码按位取反就得到反码.
补码 Complement
有 r’s complement = $r^n - D$
(n 为总的位数, D 为原来的数字)
可以写为:
$$
\displaylines
{
r^n - D = [(r^n - 1) - D] + 1
}
$$
对于 2’s complement 来说, $[(r^n - 1) - D]$ 等价于取反. 因此 2’s complement 也就是取反加一的操作.
2’s complement 可表示的范围为:
$$
\displaylines
{
-(2^{n-1}) \sim +(2^{n-1} - 1)
}
$$
2’s complement 在计算机中用来表示负数.
(补码的作用是用于表示负数,它是在原码的基础上取反再加1,以此来表示负数,可以使用补码来表示负数,从而可以减少计算机运算的复杂度。)
因此, 在计算机中, 认为 正数的原码、反码、补码都相同
原本, 对于十进制数 100 来说, 10 的补码是 90, 毕竟:
$$
\displaylines
{
100 - 10 = 90
}
$$
对于二进制数 10000 来说, 0011 的补码为:
$$
\displaylines
{
10000 - 0011 = 1101
}
$$
(也就是直接用减法算就行)
示例, 原本, -119 的表示为:
1 | |
但是计算机只能处理加法, 因此变为:
1 | |
( 11111111 + 1 就是 100000000)
而
1 | |
相当于是 01110111 取反.
因此最终为:
1 | |
^ 表示取反.
(计算机不能直接表示负数, 计算机存储负数是用其补码的形式来存储, 若要得到原本的负数, 就可以通过减一取反, 如果看到一个二进制的首位为 1, 说明其为负数的补码)
正数的原码和补码相同.
负数和正数同样通过第一位的正负判断.
$X$ 的补记为 $[X]$, 有:
$$
\displaylines
{
[x + y] = [x] + [y] \newline~ \newline
[x - y] = [x] + [-y]
}
$$
补码的加减法
用 $[x]$ 表示求 x 的补码, 则有:
$$
\displaylines
{
[x + y] = [x] + [y] \newline~ \newline
[x - y] = [x] + [-y]
}
$$
溢出
两个不同符号的数相加永远不会溢出.
两个相同符号的相加溢出, 会导致, 加数符号相同, 但和的符号不同
如, 对于四位二进制而言:
$$
\displaylines
{
(+7) + (+3) = 0111 + 0011 = 1010
}
$$
最高位为1, 表示负数.
符号位扩展
扩展以防止溢出.
将一个 n 位的 2’s complement 数扩展到 m 位.
- 如果 $m > n$, 则在左边添加 $m-n$ 位最高位
如:

- 如果 $m < n$,
编码
BCD 码
BCD (Binary Codes for Decimal Numbers), 即十进制数的二进制编码.
其又称为 8421 码 , 因为其加权规则:
- [8,4,2,1] 其实就是 $2^3, 2^2, 2^1, 2^0$
BCD码使用4位二进制数来编码一个十进制数的每个十进制位数,因此每个十进制数位上的值都可以用4位二进制数来表示,最高位的4位二进制码不表示数值,仅仅表示位值.
如十进制数23在BCD码中的表示为0010 0011。其中,左边的4位二进制码0010表示十位数值2,右边的4位二进制码0011表示个位数值3.
又如:
$$
\displaylines
{
5621_{10} = [ 0101 0110 0010 0001 ]_{BCD}
}
$$
负的 BCD 码 , 和二进制求补码方式相同, 取反加一, 如求 $-23$ 的 BCD 码:
$$
\displaylines
{
23 = 0010 0011 \newline~ \newline
^23 = 1101 1100 \newline~ \newline
^23 + 1 = 1101 1100 + 1 \newline~ \newline
= 1101 1101
}
$$
2421 码
其将 1 位十进制换为 4 位表示, 这 4 位的权重分别为: 2, 4, 2, 1.
如 $19$ 用 2421 码表示为:
$$
\displaylines
{
19 = 0001 1111
}
$$
余三码
就是十进制数加三之后转换为二进制数.
如:
1 | |
$23$ 用余三码表示为:
$$
\displaylines
{
23 \rightarrow 23 + 3 = 26 \newline~ \newline
26 \rightarrow 00011010
}
$$
二五混合码
二五混合码将每个十进制数位拆分为高位和低位,高位使用2位二进制码,低位使用5位二进制码来表示, 也就是说, 一个十进制用 7 位表示.
对于 $0 \sim 4$, 高位为 $01$.
对于 $5 \sim 9$, 高位为 $10$.
从 $0 \sim 9$, 低位以 $00001$ 依次加一得到. $9$ 为 $10000$
格雷码
Gray code, 也称为10中取1码, 二进制反射码 (Reflected Binary Code) .
格雷码是无权重码, 每一个位没有权重.
格雷码中的相邻码值, 只有一位改变:

这里, 看 3 和 4 的格雷码, 只有 1 位发生了改变. 而 3, 4 的二进制码改变了 3 位.
二进制码转换为格雷码 , 步骤为:
- 记录最高位
- 将最高位和 the next bit 相加, 记录结果
- 重复步骤
如:
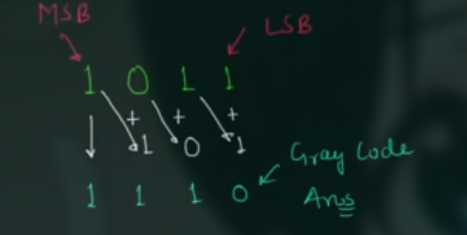
感觉就是错位相加, 如将 1110 转换为格雷码:
$$
\displaylines
{
1110 \newline~ \newline
+1110 \newline~ \newline
=001 \newline~ \newline
最终为: \newline~ \newline
1001
}
$$
布尔代数
运算和符号:
- AND ( $\cdot$ )
- OR ( $+$ )
- NOT ( $’$ )
- XOR ( $\oplus$ )
注意一个布尔方程:
$$
\displaylines
{
(x \cdot y)’ = x’ + y’ \newline~ \newline
(x+y)’ = x’ \cdot y’
}
$$
反应到电路图中, 则为: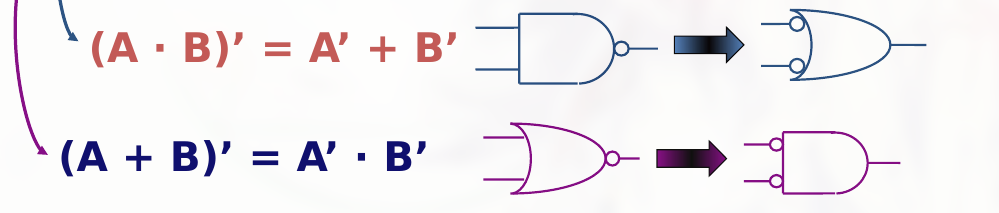
布尔代数同样满足交换律, 结合律, 分配律.
注意 同一律 , 即:
$$
\displaylines
{
X + X + … + X = X \newline~ \newline
X \cdot X \cdot … \cdot X = X \newline~ \newline
}
$$
德摩根定理
$$
\displaylines
{
(X_1 + X_2 + … + X_n)’ = X_1’ \cdot X_2’ \cdot … \cdot X_n’ \newline~ \newline
(X_1 \cdot X_2 \cdot … \cdot X_n)’ = X_1’ + X_2’ + … + X_n’ \newline~ \newline
}
$$
数学归纳法 (finite induction)
证明定理对 $n=2$ 成立, 同时证明定理对 $n = i$ 成立, 那么就可以得到定理对 $n = i + 1$ 同样成立.
反演定理 (complement of a logic expression)
反演定理又称为 广义德摩根定理
在保持计算次序不变的情况下, $+$ 变为 $\cdot$, 且变量取反.
如:
$$
\displaylines
{
(X + X \cdot Y)’ = X’ \cdot ( X’ + Y’ )
}
$$
这里的 括号 很重要. 需要保持次序不变.
对偶定理 (duality)
首先有 对偶式 的概念, 就是将 $+$ 换成 $\cdot$, $\cdot$ 换成 $+$, 然后在保持计算次序不变的情况下变量取反得到的式子.
对偶定理 : 两式逻辑式相等, 则它们的对偶式也相等.
德摩根定理其实就是对偶定理的简单推广.
应用:
若要证明两个逻辑式相等, 可以证明其对偶式相等, 如证明:
$$
\displaylines
{
A + BC = (A + B)(A + C)
}
$$
则可证明:
$$
\displaylines
{
(A + BC)’ = [(A + B)(A + C)]’ \newline~ \newline
(A + BC)’ = A’ \cdot (B’ + C’) \newline~ \newline
[(A + B)(A + C)]’ = (A’ \cdot B’) + (A’ \cdot C’) \newline~ \newline
= A’ \cdot (B’ + C’)
}
$$
正逻辑约定和负逻辑约定
正逻辑约定 (Positive-Logic) 为: $F = A \cdot B$
负逻辑约定 (Negative-Logic) 为: $F = A + B$
其互为对偶式:

逻辑函数的标准表示方法
逻辑函数 如:
$$
\displaylines
{
Y = F(A,B,C) = A \cdot (B + C)
}
$$
逻辑电路如 :
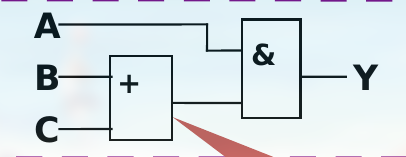
真值表 如:

波形图 如:
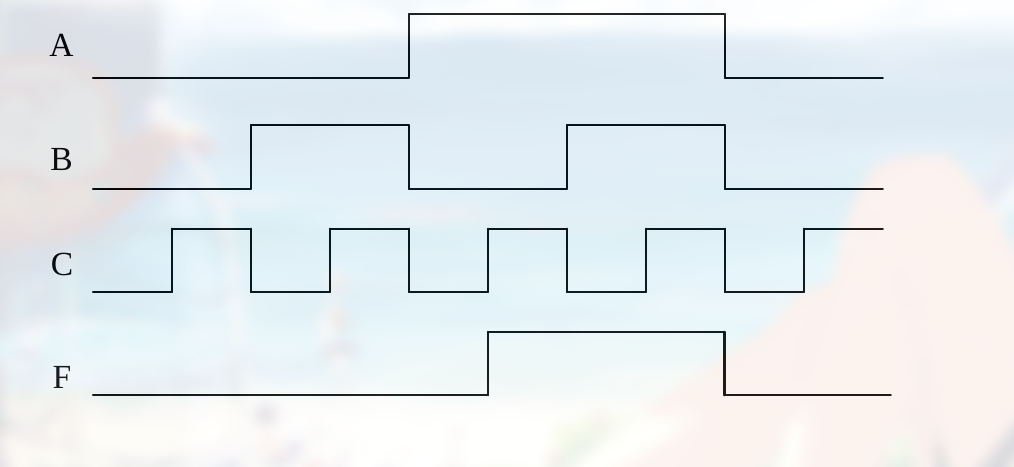
Topic2 数字设计的原则
SOP, Sum of Products.
Karnaugh map 比较重要.
几个逻辑门的符号:
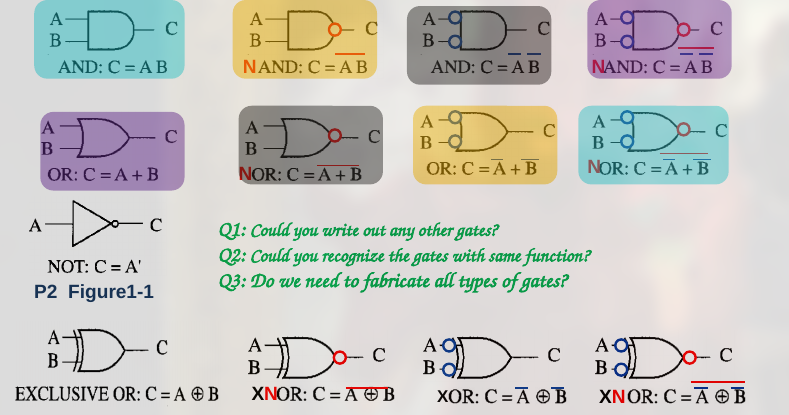
逻辑函数的基本形式 (这里是取反后的变换):
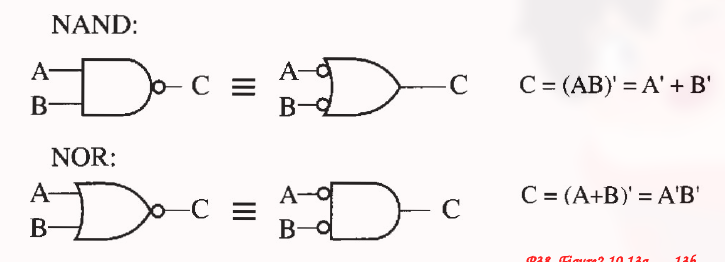
根据电路图画出真值表, 逻辑电路以及写出逻辑表达式, 如:
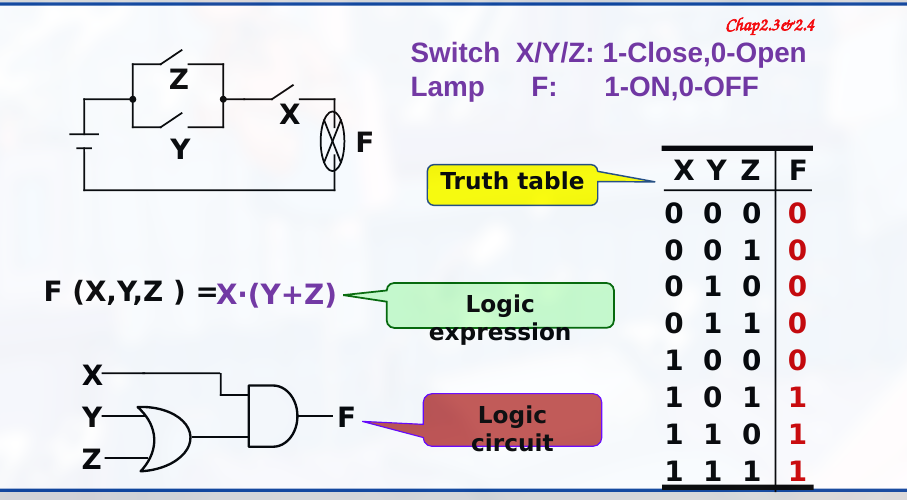
全加器
其 logic symbol 为:
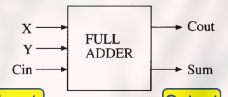
有两个二进制输入 X 和 Y, Cin 指的是 carry 位, 也就是进位.
输出为 Sum, 以及 Cout (carry out, 进位)
输出的逻辑表达式可以写为:
$$
\displaylines
{
Cout = X’YCin + XY’Cin + XYCin’ + XYCin \newline~ \newline
Sum = (X+Y+Cin)(X+Y’+Cin’)(X’+Y+Cin’)(X’+Y’+Cin)
}
$$
( 为什么这样列? )
Karnaugh map (K’ Map)
Karnaugh map(K-map)是一种在数字逻辑和电路设计中用于简化布尔表达式的工具。它是由美国数学家Maurice Karnaugh于1953年发明的。
K-map的主要作用是通过可视化的方式展示布尔函数的真值表,并提供了一种方法来优化布尔表达式。通过对相邻的1进行分组,可以将布尔表达式简化为更简单的形式,从而减少逻辑门的数量和延迟,并提高电路的性能和可靠性。
如, 用一个布尔表达式, 画出其真值表:

( 总的组合数, 这里为 8 种, 因为有 3 个变量, 每个变量有 2 个值, 因此总的有 $2^3$ 种组合 )
技巧
只要输入中有 0, 输出就为 1, 用 与非门 .
minterm 中的下标和 K’Map 中的对应关系.
异或门, 用来构建 1’bit 的比较器.
异或, 也就是相异才输出 1.
同或, 也就是相同才输出 1.
串联电路缺点, 时间延时长. 但其结构简单.
D 触发器, J-K 触发器
$Q^* = D$
圈, 多半是计数器.
没输入, 用来判断哪一个集.
上课知识点
CISC (Complex Instruction Set Computer) 是复杂指令集. 如 x86
RISC (Reduced Instruction Set Computer) 是简单指令集. 如 ARM
ADC 的精度由其位数表示.
复习课
正数的原码, 反码, 补码都是一样的.
K’Map 化简加上 Don’t Care 一定会考.
Verilog/HDL 语言一定会考.
逻辑门辨认以及画出其真值表.
注意 SOP 和 POS.
151 器件, 151 实现组合逻辑电路. 实现 4 变量.
K’Map 降维的方法.
译码器能实现 3 位组合逻辑函数.
151 比 138 高.
PPT 上的波形图, 仔细看.
Verilog 组合逻辑用存储器实现.
moore 集和 mealy 集.
时序逻辑电路分析.
计数器重点是 163.
序列发生器.
双稳态器件, 非常重要.
S-R Latch 中 S 指 “Set”, R 指 “Reset”.
D-Latch
Flip-Flops, D 触发器.
移位寄存器.
194 是什么.
拆环方法.
小知识点
Moore 和 Mealy 名称的由来
Moore和Mealy是两位著名的电子工程师,他们都对有限状态机的理论和应用做出了重要贡献,因此有限状态机中的Moore型和Mealy型得名于他们。
Moore型有限状态机是由美国电气工程师Edward F. Moore在1956年提出的。在Moore型有限状态机中,输出只取决于当前状态,与输入无关。Moore型有限状态机通常用于输出较为简单的应用,例如闪烁灯、计数器等。
Mealy型有限状态机是由美国电气工程师George H. Mealy在1955年提出的。在Mealy型有限状态机中,输出不仅取决于当前状态,还取决于输入。Mealy型有限状态机通常用于输出较为复杂的应用,例如通信协议、控制系统等。
什么是激励方程
在有限状态机(FSM)中,激励方程是指控制状态转移的输入信号的逻辑表达式。这些输入信号通常被称为“激励”或“输入变量”,它们的值决定了状态机的行为。
因此,激励方程是描述输入信号与状态转移之间关系的逻辑表达式,通常使用布尔代数或逻辑运算符来表示。激励方程的值决定了状态机在给定状态下是否转移到下一个状态,以及是否产生输出。
在Moore型有限状态机中,激励方程只取决于当前状态,因为输出只与当前状态有关。而在Mealy型有限状态机中,激励方程不仅取决于当前状态,还取决于输入信号。
需要注意的是,激励方程并不等同于输入信号的表达式。输入信号可能包括多个变量,因此激励方程通常需要对这些变量进行逻辑运算,以确定是否需要进行状态转移以及产生什么样的输出信号。
总之,激励方程是描述输入信号与状态转移之间关系的逻辑表达式,在有限状态机的设计过程中非常重要。
激励方程中的变量通常是有限状态机的输入信号,但不一定是全部的输入信号。在有限状态机的设计中,可能存在多个输入信号,但只有一部分输入信号参与状态转移和输出的逻辑运算,这些输入信号就是激励方程中的变量。
因此,可以说激励方程中的变量是输入信号的一个子集。这些变量的逻辑运算结果决定了状态机的行为,包括状态转移和输出信号的产生。
需要注意的是,有限状态机的输入信号可能包括多个变量,每个变量都可以使用逻辑表达式来表示。因此,在实际设计中,可能需要编写多个激励方程来表示不同的输入变量之间的逻辑关系。
总之,激励方程中的变量是有限状态机的输入信号的一个子集,它们的逻辑运算结果决定了状态机的行为。
什么是 Flip-Flop
Flip-flop是指一类数字电路中常用的存储元件,也可以称为触发器。不同类型的Flip-flop具有不同的特点和应用场景,但它们都能够存储一个二进制状态,并能够根据时钟信号的边沿进行触发,从而实现状态的转移或保持。因此,Flip-flop可以被视为一类数字电路中常用的器件。
什么是 DFF
D-Flip-Flop是一种特殊的flip-flop,它只有一个输入端口D,一个时钟信号端口CLK和两个输出端口Q和Q’。D-Flip-Flop的功能是在时钟信号的上升沿(或下降沿)的时候,将D端口的输入数据存储到Q端口,并将Q’端口的输出数据与Q端口的反相输出相连。
D-Flip-Flop是最常用的flip-flop之一,它的输入端口和时钟端口分离,使得设计者可以灵活地控制数据输入的时机,从而实现各种不同的功能。例如,可以将多个D-Flip-Flop级联在一起,构成移位寄存器,用于数据的移位操作;可以将D-Flip-Flop组合在一起,构成计数器,用于计数操作。
什么是 latch
“Latch”是英语单词,可以翻译为“锁定”、“锁住”等含义。在数字电路中,Latch通常指数据锁存器,是一种能够锁定输入数据并保持输出状态的电路元件。Latch的输出状态可以在时钟信号的任意时刻更新,而与时钟信号的边沿无关。
Latch的名称来源于其特性,即可以锁定输入的数据,并保持输出状态,类似于一把锁可以把门锁住,防止门被打开或关闭。Latch通常由若干个逻辑门组成,根据不同的触发方式和时钟信号的控制方式,可以分为SR Latch、D Latch、Gated Latch等多种类型,应用广泛。
需要注意的是,Latch和Flip-flop虽然都是数字电路中常用的存储元件,但它们的功能和使用方式有所区别。Flip-flop通常用于时序电路中,可以在时钟边沿触发状态转移,而Latch可以在任意时刻更新其输出状态,更加灵活。
什么是 D-latch
D Latch是一种数字电路中的存储元件,也可以称为数据锁存器。与D-Flip-Flop类似,D Latch也可以存储一个二进制状态,并且可以根据时钟信号的变化来控制状态的保持或转移。
一个D Latch通常由两个逻辑门(例如,一个反相器和一个与门)组成,其中一个门用于控制状态的保持,另一个门用于控制状态的转移。D Latch的输入端口是D,表示要存储的二进制状态;输出端口是Q,表示存储的状态值;时钟信号通常被连接到使能端口EN。
当时钟信号EN为高电平时,D Latch处于工作状态,此时输入的数据D会被存储到内部的存储单元中,并且输出端口Q的值等于D的值;当时钟信号EN为低电平时,D Latch处于锁存状态,此时输入的数据D不会影响输出端口Q的值,输出端口Q的值保持不变。
D Latch与D-Flip-Flop的不同之处在于,D Latch的输出端口Q是直接与输入端口D相连的,而不是通过时钟信号控制。因此,D Latch可以在时钟信号的任意时刻更新其输出状态,而D-Flip-Flop只能在时钟信号到达时更新其输出状态。这使得D Latch在一些特定的应用场景中更加灵活,例如用于实现时序逻辑电路或者控制电路中的数据锁存操作。
什么是主从 D-latch
主从 D-Latch是一种存储器件,用于在数字电路中存储一个比特(0或1)。它由两个逻辑门(主门和从门)组成,可以通过一个时钟信号来控制存储器的读写操作。
主从D-Latch的输入端包括数据输入(D)和时钟输入(CLK)。当时钟输入为高电平时,主门会将数据输入传输到从门,从门的输出将被锁定,并且可以被读取。当时钟输入为低电平时,主门的输出将不会传输到从门,从门的输出将被保持不变。