GATE-Solved-Problems-Notes
Youtube GATE Solved Problems 系列视频
1 数字系统
例 1, 用另一种等价的 2’s complement 来表示一个 2’s complement number
1101.
其含义其实就是利用符号位扩展来表示. 如这里的 1101 是 4 位, 另一种等价形式就可以是 6 位, 也就是 111101 ( 负数用 1 来扩展, 正数用 0 来扩展 )
例 2, 两个 2’s complement numbers 的 sign bits 为
x和y,x与y的和为z, 求表示 overflow 发生的 Boolean function
2’s complement 数的范围为 $-2^{n-1} \sim 2^{n-1} - 1$
两种情况被定义为 overflow:
- 两个正数相加, 结果为负数
- 两个负数相加, 结果为正数
有:
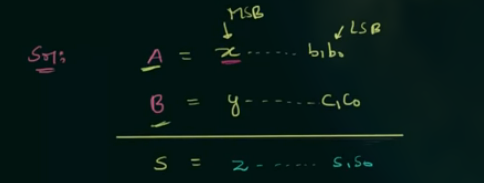
对于第一种情况 (两个正数相加, 结果为负数), 有:
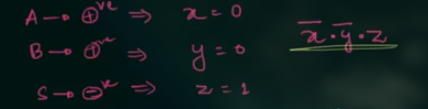
其 Boolean function 为 $\overline{x} \cdot \overline{y} \cdot z$.
对于第二种情况 (两个负数相加, 结果为正数), 有:
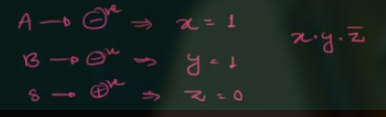
其 Boolean function 为 $x \cdot y \cdot \overline{z}$
由于两种情况其中一个发生即可, 因此为 AND, 即:
$$
\displaylines
{
\overline{x} \cdot \overline{y} \cdot z + x \cdot y \cdot \overline{z}
}
$$
例 3, 一个 4-bit 2’s complement 表示的一个 decimal number 为 1000, 求这个数是多少.
需要有这样的一个概念:
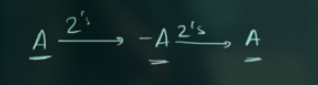
一个数, 做两次 2’s complement 可以得到其本身.
例 4, 一个 signed decimal numbers 用 1’s complement 表示的范围为多少.
对于 signed decimal numbers 来说, 其 1’s complement 的范围为:
$$
\displaylines
{
-(2^{n-1 - 1} \sim +(2^{n-1} - 1))
}
$$
因为, 最大数为: 011...11, 其值为 $2^{n-1} - 1$.
最小数为: 111...11, 其值为 $-(2{n-1} - 1)$
因为此时最高位表示符号.
关于 1’s complement 和 2’s complement 名称的由来
1’s complement 表示法是因为负数的表示是通过将其对应的正数取反得到的,即把每一位上的 0 变成 1,把 1 变成 0,所以称为 1’s complement。而 2’s complement 表示法的名字则是因为负数的表示是通过将其对应的正数取反后加 1得到的,即相当于对其进行了两次取反操作,所以称为 2’s complement。
例5
11001,1001,11101都是一组数的 2’s complement representation, 那么这组数是什么
除了重复的 MSB 以外, 其他每一位都相同, 那么这个二进制数表示同一个数.
如, 这里的:

都表示 -7.
推导如下:
$$
\displaylines
{
4 位表示 -7 为 \newline~ \newline
1001 \newline~ \newline
5 位表示 -7 为 \newline~ \newline
11001 \newline~ \newline
(将 4 位扩展到 5 位, 将符号位扩展) \newline~ \newline
6 位表示 -7 \newline~ \newline
111001 \newline~ \newline
.
.
}
$$
例7 Decimal 43 的 16 进制和 BCD 码表示
十进制转换为十六进制, 可以直接进行转换:
$$
\displaylines
{
43 \div 16 = 2 … 11 \newline~ \newline
2 \div 16 = 0 … 2 \newline~ \newline
结果就为: \newline~ \newline
2B
}
$$
十进制转换为 BCD 码, 就是将十进制的每一位, 用 4 位二进制表示, 即:
$$
\displaylines
{
4 = 0100, 3 = 0011 \newline~ \newline
43 = 0100 0011
}
$$
例8 两个 2’s complement 数 $P = 11101101$, $Q = 11100110$ 相减的 2’s complement 表示为多少
$$
\displaylines
{
P - Q = P + (-Q) \newline~ \newline
= P + ( 2’s\ complement\ of\ Q ) \newline~ \newline
= 11101101 + 00011010 \newline~ \newline
= 0000 0111
}
$$
对于 2’s complement 而言, overflow 常常被忽略.