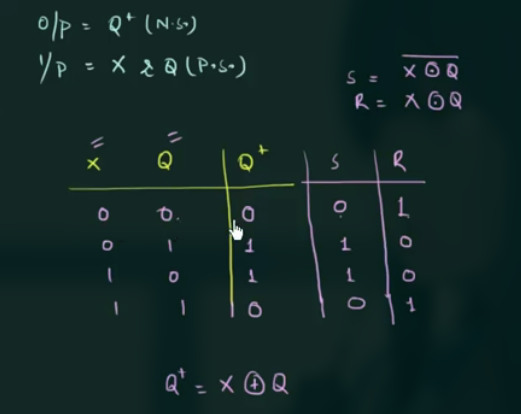Youtube-Digital-Electronics-Notes
1 什么是信号
一个信号是一个函数, 其表示物理量由其他因素 (时间, 距离等) 引起的变化.
如:
$$
\displaylines
{
F(x) = -a x^2 + bx + c
}
$$
这里, 信号就是 $F$, 而其受 $x$ 的影响.
在 electrical and electronic 中, 信号常常指 electrical quantity (一般是 I, V) 随时间的变化.
如果 I 在不同的时间保持一致, 那么其不是一个 信号, 而是 DC (direct current).
2 什么是模拟信号
一个模拟信号是连续的, 其 is defined for infinite number of points even when it is in finite interval.
模拟信号与数字信号的区别, 如下面两个 clock:

模拟信号是连续的, 而数字信号是离散的.
即, 数字 1 变为 数字 2, 其是跳跃的, 而不是连续变化的.
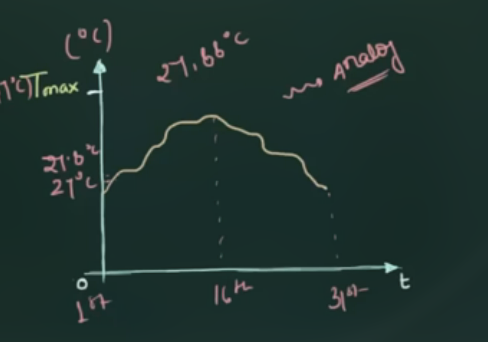
一个模拟信号的例子, 温度, 其可以取到区间内的所有值:
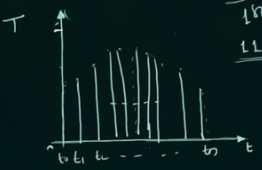
离散时间信号 (discrete time signal) 指, 信号被定义在离散的时间区间中.
一个例子为:
3 什么是数字信号
此时, 信号的值是分为一个一个的 level ( 就和量子力学中的光子一样, 一份一份的 ), 而不是连续的, 如:
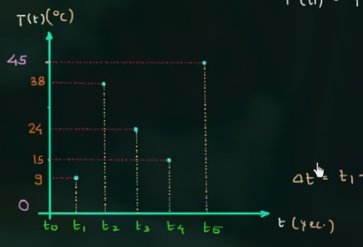
对于数字信号而言, level 越多 (越密集), 其误差越小 ( 也就是像微积分一样, 份数越多, 越能近似为模拟信号 )
4 数字信号的需要
所有生活中的信号都是 analog.
将模拟信号转换为数字信号需要 ADC (Ananog Digital Converter).
数字信号用于在 conmmunication process 中最小化 noise (也就是 unwanted signal)
这个消除 noise, 需要在 noise 很小时才会有效果, 如:
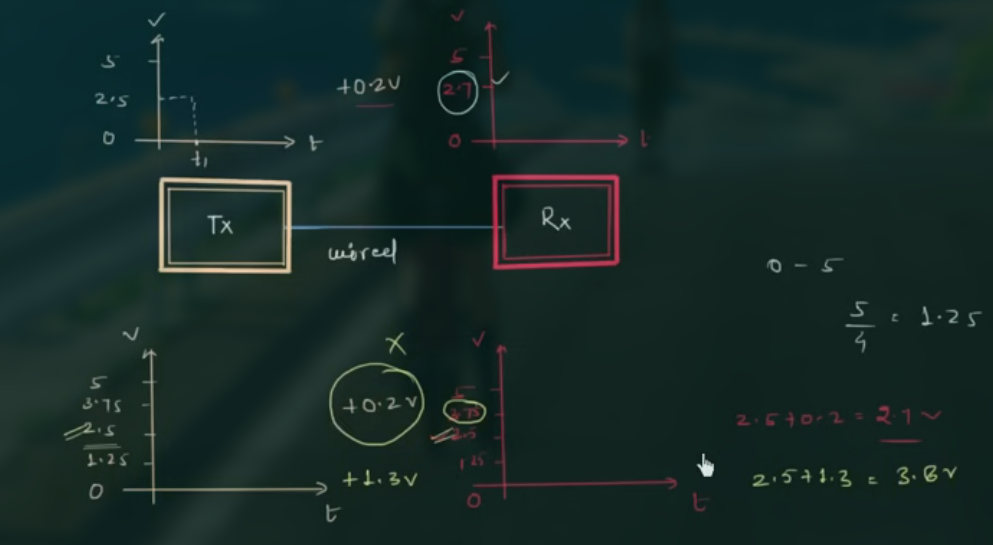
其中, Tx 指 transmiter, Rx 指 receiver, 中间为 wire.
假设要传输的信号为 $2.5V$, 但是有 $0.2V$ 的 noise, 因此实际传输的为 $2.7V$.
receiver 接受的信号有 5 个 lever, 分别为 $0, 1.25, 2.5, 3.75, 5$, 接收到的信号为 $2.7V$, 但是没有这个 level, 因此其被视为第一层的 level, 也就是 $2.5V$, 此时 noise 就被消除了. (但对于大的 noise 就不管用了, 如 $1.2V$ )
5 数电简介
结构大概为:
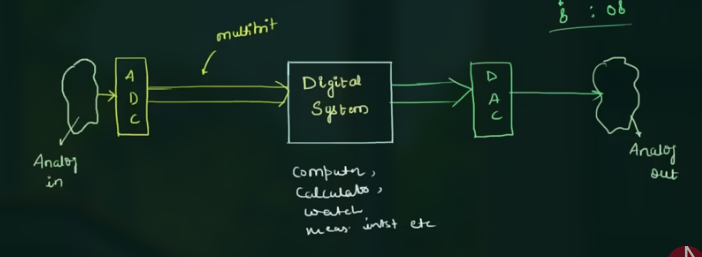
由 AnalogIn 获取外界的输入, 通过 ADC (Analog Digital Converter) 转化为数字信号 (比特流), 传递给 digital system 进行处理, 处理结果通过 DAC (Digital Analog Converter) 转化为模拟信号并传递给 AnalogOut
而一个 digital system 又有如下结构:
Digital system -> Sub system -> Module -> Basic unit (logic gate) -> circuit (transister, capaciter …)
6 Switch and Bits Intuition
数字系统 (digital system) 的优点:
- noise immunity
- use less bandwidth
- encryption
- efficiency is higher for long distance transmission
通过增加 level 数来增加精度.
可以用二进制来表示 Switch 的状态, 0 表示关闭, 1 表示开启.
若电路中有 3 个 switches, 则会有 8 中状态, 即 $2^3$ (每个开关两种状态, 3 个就是 $2^3$ 种状态 )
7 布尔代数
布尔代数是一组规则, 用于在不影响其作用的情况下简化逻辑表达式.
其一般用于变量较少时.
如, 将:
$$
\displaylines
{
F = AB + BC + ABC
}
$$
简化为:
$$
\displaylines
{
F = A’B + BC
}
$$
逻辑表达式所用的逻辑门数量减少.
什么是逻辑表达式
逻辑表达式指的是由逻辑运算符和逻辑变量组成的表达式,用来表示逻辑运算的结果。逻辑运算符包括非(NOT)、与(AND)、或(OR)三种,它们的运算结果只有真(True)和假(False)两种可能。
其可以用来描述逻辑门的组合, 如:
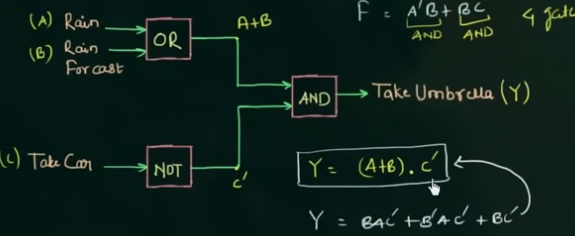
几个 rules:
complement: A 的 complement 为 $\overline{A}$ 或 $A’$ 或 $not\ A$
AND: $A \cdot B$, 有:
$$
\displaylines
{
A \cdot A = A \newline~ \newline
A \cdot A’ = 0 \newline~ \newline
A \cdot 0 = 0 \newline~ \newline
A \cdot 1 = 1
}
$$
- OR: $A + B$, 有:
$$
\displaylines
{
A + A = A \newline~ \newline
A + A’ = 1 \newline~ \newline
A + 0 = A \newline~ \newline
A + 1 = 1
}
$$
- Distributive law (分配率):
$$
\displaylines
{
A \cdot (B + C) = A \cdot B + A \cdot C \newline~ \newline
A + (B \cdot C) = (A + B) \cdot (A + C)
}
$$
上述两个式子可以推导出:
$$
\displaylines
{
A + \overline{A} B = A + B \newline~ \newline
\overline{A} + AB = \overline{A} + B
}
$$
- commutative law (交换率):
$$
\displaylines
{
(A \cdot B) \cdot C = A \cdot (B \cdot C)
}
$$
优先级:
NOT
AND
OR
De Morgans law (德摩根定理):
$$
\displaylines
{
\overline{(A + B)} = A’ \cdot B’ \newline~ \newline
\overline{A \cdot B} = A’ + B’
}
$$
一个化简逻辑表达式的例子
$$
\displaylines
{
Y = BAC’ + B’AC’ + BC’ \newline~ \newline
= AC’ (B + B’) + BC’ \newline~ \newline
= AC’ + BC’ \newline~ \newline
= (A+B) C’
}
$$
( $B + B’ = 1$ )
8 化简布尔代数的例子
化简布尔代数也称为 minimise 这个表达式.
$F = A \cdot B + A \cdot B’$
$$
\displaylines
{
F = A \cdot B + A \cdot B’ \newline~ \newline
= A \cdot (B + B’) \newline~ \newline
= A
}
$$
$F = A \cdot B + A \cdot B’ \cdot C + A \cdot B’ \cdot C’$
$$
\displaylines
{
F = A \cdot B + A \cdot B’ \cdot C + A \cdot B’ \cdot C’ \newline~ \newline
= A \cdot ( B + B’ \cdot C + B’ \cdot C’ ) \newline~ \newline
= A \cdot ( B + C + B’ \cdot C’ ) \newline~ \newline
= A \cdot ( B + C + C’ ) \newline~ \newline
= A \cdot ( B + 1 ) \newline~ \newline
= A \cdot 1 \newline~ \newline
= A
}
$$
下面两个例子, 主要利用了:
$$
\displaylines
{
A + \overline{A} B = A + B \newline~ \newline
\overline{A} + AB = \overline{A} + B
}
$$
$F = (A + B + C)(A + B’ + C)(A + B + C’)$
$$
\displaylines
{
F = (A + B + C)(A + B’ + C)(A + B + C’) \newline~ \newline
= (A + B + C)(A + B + C’)(A + B’ + C) \newline~ \newline
= [(A + B) + C \cdot C’](A + B’ + C) \newline~ \newline
= (A + B + 0)(A + B’ + C) \newline~ \newline
= (A + B)(A + B’ + C) \newline~ \newline
= [A + B \cdot (B’ + C)] \newline~ \newline
= A + B \cdot B’ + B \cdot C \newline~ \newline
= A + B \cdot C
}
$$
$F = (A + B)(A + B’)(A’ + B)(A’ + B’)$
$$
\displaylines
{
F = (A + B)(A + B’)(A’ + B)(A’ + B’) \newline~ \newline
= (A + B \cdot B’) (A’ + B \cdot B’) \newline~ \newline
= (A + 0) (A’ + 0) \newline~ \newline
= A \cdot A’ \newline~ \newline
= 0
}
$$
9 冗余定理 Redundancy Theorem
这是一个 trick 来化简逻辑表达式, 如, 将:
$$
\displaylines
{
Y = AB + A’C + BC
}
$$
化简为:
$$
\displaylines
{
Y = AB + A’C
}
$$
以及:
$$
\displaylines
{
Y = (A+B) (A’+C) (B+C) new
}
$$
化简为:
$$
\displaylines
{
Y = (A+B)(A’+C)
}
$$
需要四个条件才能使用:
- Three variable, 三个变量 (如上式中的A, B, C)
- Each variable is repeated twice, 每一个变量出现两次 (包括 complement 形式, 如 A 和 $A’$)
- One variable is complemented, 其中一个包含 complement 形式 (如这里的 A 和 $A’$)
- Take the complemented variable, 也就是化简的步骤为, 将有 complemented 的变量提出
证明
$$
\displaylines
{
Y = AB + A’C + BC \newline~ \newline
= AB + A’C + BC \cdot 1 \newline~ \newline
= AB + A’C + BC \cdot (A + A’) \newline~ \newline
= AB + A’C + ABC + A’BC \newline~ \newline
= AB[1 + C] + A’C[1 + B] \newline~ \newline
= AB + A’C
}
$$
应用 Redundancy Theorem:
例1
$$
\displaylines
{
F = AB + BC’ + AC \newline~ \newline
F = C’B + C’A
}
$$
例2
$$
\displaylines
{
F = AB’ + BC + AC \newline~ \newline
= B’A + BC
}
$$
例3
$$
\displaylines
{
F = (A + B)(A’ + C)(B + C) \newline~ \newline
= (A+B)(A’+C)
}
$$
例4
$$
\displaylines
{
F = (A+B) (B’+C) (A+C)
}
$$
例5
$$
\displaylines
{
F = A’B’ + AC’ + B’C’
}
$$
10 SOP Form
SOP 指 Sum of Product.
将一个真值表转换为 SOP From.
只写出 $Function = 1$ 的 Product, 如:
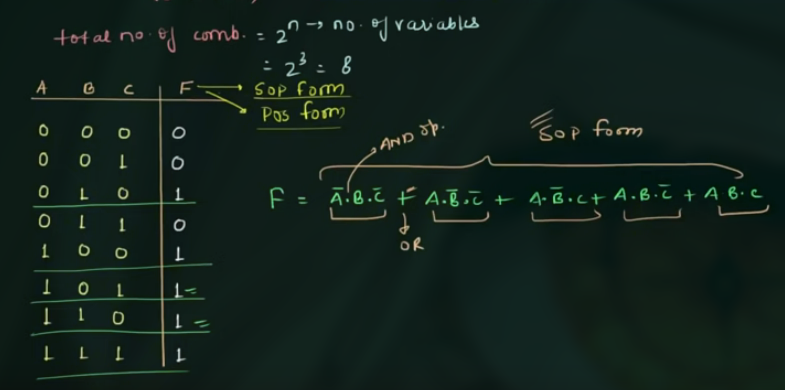
这里 $A,B,C$ 表示 1, $\overline{A},\overline{B},\overline{C}$ 表示 0.
上述形式也称为 Standard Canonical SOP-Form (即, 直接通过真值表写出的式子).
在数字电路中,一个布尔函数可以通过一组变量和它们的逻辑运算符表示。布尔函数的每一个可能的输出称为一个“项”(term)。
一个 minterm 是指在布尔函数中,使得布尔函数等于 1 的最小项。minterm 是指一个包含所有输入变量的布尔乘积。 例如,对于三个输入变量 A、B 和 C,其中 A=1,B=0 和 C=1,那么它的 minterm 是 ABC。每个布尔函数都可以表示为其所有 minterm 的和。
相反,一个 maxterm 是指在布尔函数中,使得布尔函数等于 0 的最大项。maxterm 是指一个包含所有输入变量的布尔和积。例如,对于三个输入变量 A、B 和 C,其中 A=1,B=0 和 C=1,那么它的 maxterm 是 A+B+C。每个布尔函数都可以表示为其所有 maxterm 的乘积。
因此,一个布尔函数可以有多种表示方式,包括使用它的 minterm 或 maxterm 表示。
minterm (最小项), 用 m (小m) 表示.
maxterm (最大项), 用 M (大M) 表示.
找到 minimal SOP Form, 也就是化简 SOP From.
如, 化简如下 SOP Form:
$$
\displaylines
{
F = \overline{A}B\overline{C} + A\overline{B}\overline{C} + A \overline{B} C + AB\overline{C} + ABC \newline~ \newline
= \overline{A}B\overline{C} + A\overline{B}[\overline{C} + C] + AB[\overline{C} + C] \newline~ \newline
= \overline{A} B \overline{C} + A\overline{B} + AB \newline~ \newline
= \overline{A} B \overline{C} + A[\overline{B} + B] \newline~ \newline
= \overline{A} B \overline{C} + A \newline~ \newline
= A + B\overline{C}
}
$$
可以知道, 有两种 SOP Form:
- Standard Canonical SOP-Form (每一个 minterm 包含所有的变量, normal 形式或者 complemented 形式), 如:
$$
\displaylines
{
F = \overline{A}B + AB + \overline{A} \overline{B}
}
$$
(这里有两个变量 – $A,B$)
- minimal SOP Form (每一个 minterm 不包含所有的变量, normal 形式或者 complemented 形式), 如:
$$
\displaylines
{
F = A + \overline{B} C
}
$$
(这里有三个变量 – $A,B,C$)
例题 对于下列给定的真值表, 最小化 SOP expression

同样:
$$
\displaylines
{
1 \rightarrow A,B \newline~ \newline
0 \rightarrow \overline{A},\overline{B}
}
$$
从真值表中, 找出 function 值为 1 的组合:
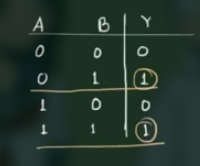
, 写为:
$$
\displaylines
{
Y = \overline{A} B + A B
}
$$
开始化简:
$$
\displaylines
{
Y = \overline{A} B + A B \newline~ \newline
= B (\overline{A} + A) \newline~ \newline
= B \cdot 1 \newline~ \newline
= B
}
$$
此时, 找到了 $Y$ 和 $A,B$ 的关系式, 即 $Y = B$, 可以带回真值表中检查.
例题 简化以下形式 $Y(A,B) = \sum m (0,2,3)$
即:
$$
\displaylines
{
Y = m_0 + m_2 + m_3 \newline~ \newline
= \overline{A} \overline{B} + A \overline{B} + AB \newline~ \newline
= (\overline{A} + A) \overline{B} + AB \newline~ \newline
= 1 \cdot \overline{B} + AB \newline~ \newline
= \overline{B} + AB \newline~ \newline
= \overline{B} + A
}
$$
11 POS Form
POS Form 指 Product of Sum.
其用于, 当 output 为 low 或者 0 时.
用一个真值表写出 POS From:

先找出 $function = 0$ 的组合.
对于 POS Form, 有:
$$
\displaylines
{
0 \rightarrow A \newline~ \newline
1 \rightarrow \overline{A}
}
$$
(和 SOP Form 相反)
从上述真值表中有:
$$
\displaylines
{
Y = (A + B + C) (A + B + \overline{C}) (A + \overline{B} + \overline{C})
}
$$
其中 $(A+B+C)$, $(A+B+\overline{C})$, $(A+\overline{B}+\overline{C})$ 这些称为 maxterm .
这里的 minterm 为:
$$
\displaylines
{
\overline{Y} = \overline{A} \overline{B} \overline{C} + \overline{A}\overline{B}C + \overline{A}BC
}
$$
( 这里同样是取得 $function=0$, 不知道为啥, 暂时理解为, 将 POS From 写为 SOP From, 就是取反 )
同样有两种 POS Form:
- Standard/Canonical SOP-Form (包含所有变量)
- minimal SOP-Form (不包含所有变量, 化简后的形式)
将上述 Standard SOP-Form 化简为 minimal SOP-Form, 如;
$$
\displaylines
{
Y = (A + B + C) (A + B + \overline{C}) (A + \overline{B} + \overline{C}) \newline~ \newline
= (A+B+C\overline{C}) (A+\overline{B}+\overline{C}) \newline~ \newline
= (A+B)(A+\overline{B}+\overline{C}) \newline~ \newline
= A + B (\overline{B}+\overline{C}) \newline~ \newline
= A + B\overline{B} + B\overline{C} \newline~ \newline
= A + B \overline{C} \newline~ \newline
= (A+B) (A+\overline{C})
}
$$
例子, 找出下列真值表的 POS expression (两个形式)
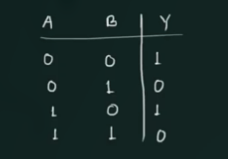
同样注意, 对于 POS From 而言, 有:
$$
\displaylines
{
0 \rightarrow A \newline~ \newline
1 \rightarrow \overline{A}
}
$$
因此, Canonical Form of POS 为:
$$
\displaylines
{
Y = (A+\overline{B}) (\overline{A}+\overline{B})
}
$$
同样可以写为:
$$
\displaylines
{
Y = \prod(M_1,M_3) \newline~ \newline
or \newline~ \newline
Y = \prodM(1,3)
}
$$
这个真值表的 minterm 可以写为:
$$
\displaylines
{
Y = \sum m(0,2)
}
$$
minimal form 为:
$$
\displaylines
{
Y = (A+\overline{B}) (\overline{A}+\overline{B})
= \overline{B} + A \overline{A} \newline~ \newline
= \overline{B} + 0 \newline~ \newline
= \overline{B}
}
$$
使用 SOP 和 POS Form 的原因 :
- 如果想使用更多的 AND gates, 就用 SOP Form
- 如果想使用更多的 OR gates, 就用 POS Form
12 SOP & POS Form Example
例子, 写出下列真值表的 SOP 和 POS form

对于 SOP Form, 可以写为:
$$
\displaylines
{
Y(A,B,C) = \sum m (0,2,3,6,7) \newline~ \newline
0 \rightarrow \overline{A} \newline~ \newline
1 \rightarrow A \newline~ \newline
Y(A,B,C) = \overline{A}\overline{B}\overline{C} + \overline{A}B\overline{C} + \overline{A}BC + AB\overline{C} + ABC \newline~ \newline
(Canonical SOP Form) \newline~ \newline
化简如下: \newline~ \newline
Y = \overline{A}\overline{B}\overline{C} + \overline{A}B(\overline{C}+C) + AB(\overline{C}+C) \newline~ \newline
= \overline{A}\overline{B}\overline{C} + \overline{A}B \cdot 1 + AB \cdot 1 \newline~ \newline
= \overline{A}\overline{B}\overline{C} + B(\overline{A} + A) \newline~ \newline
= \overline{A}\overline{B}\overline{C} + B \newline~ \newline
= B + \overline{A}\overline{C} \newline~ \newline
(minimal SOP Form)
}
$$
对于 POS Form 可以写为:
$$
\displaylines
{
Y = (A,B,C) = \prod M(1,4,5) \newline~ \newline
0 \rightarrow A \newline~ \newline
1 \rightarrow \overline{A} \newline~ \newline
Y = (A + B + \overline{C}) + (\overline{A} + B + C) (\overline{A} + B + \overline{C}) \newline~ \newline
(Canonical POS Form) \newline~ \newline
化简如下: \newline~ \newline
Y = (A + B \overline{C}) (\overline{A} + B + C\overline{C}) \newline~ \newline
= (A + B \overline{C}) (\overline{A} + B + 0) \newline~ \newline
= (A + B \overline{C}) (\overline{A} + B) \newline~ \newline
= (B + \overline{A}(A+\overline{C})) \newline~ \newline
= B + \overline{A}\overline{C} \newline~ \newline
= (B + \overline{A}) (B + \overline{C})
}
$$
13 Minimal to Canonical Form Comversion
也就是将 minimal 形式转化为 Standard 形式.
步骤:
- 找出有多少个变量
- 找出每一项中缺失的变量
- 对于 SOP Form 来说, 将缺失的变量当作 $A + \overlinePA$ 展开; 对于 POS Form 来说, 将缺失的变量当作 $A \overline{A}$ 展开
- 去除重复项
SOP Form 的Minimal to Canonical Form的转化
如 $Y = A + \overline{B}C$:
- 变量一共有 $A,B,C$
- 缺失为: $Y = A \cdot 1 \cdot 1 + \overline{B}C \cdot 1$
- 展开为: $Y = A (B + \overline{B}) (C + \overline{C}) + \overline{B}C (A + \overline{A})$ \newline~ \newline
- 最终化简为: $Y = ABC + AB\overline{C} + A\overline{B}C + A\overline{B}\overline{C} + \overline{A}\overline{B}C$
POS Form 的Minimal to Canonical Form的转化
如: $F = (A + B + \overline{C})(\overline{A} + C)$
有:
- 变量一共有 $A,B,C$
- 缺失为: $F = (A + B + \overline{C})(\overline{A} + C + 0)$
- 展开为: $F = (A + B + \overline{C})(\overline{A} + C + B \overline{B})$
得到:
$$
\displaylines
{
F = (A + B + \overline{C})(\overline{A} + C + B \overline{B}) \newline~ \newline
= (A + B + \overline{C}) (\overline{A} + C + B) (\overline{A} + C + \overline{B})
}
$$
Examples & Trics (SOP & POS Forms)
例1, 从一个 minimal SOP Form 找出 logic expression $A + \overline{B}C$ 中的 minterm 数量
思路: 先由 minimal SOP Form 求出 Canonical Form, 然后再数
$$
\displaylines
{
F = A + \overline{B} C \newline~ \newline
= A (B+\overline{B}) (C+\overline{C}) + \overline{B}C (A + \overline{A}) \newline~ \newline
= ABC + AB\overline{C} + A\overline{B}C + A\overline{B}\overline{C} + A\overline{B}C + \overline{A}\overline{B}C \newline~ \newline
= ABC + AB\overline{C} + A\overline{B}\overline{C} + A\overline{B}C + \overline{A}\overline{B}C \newline~ \newline
}
$$
因此有 5 项.
例2, 对于包含两个变量的 logic expression, minterm 和 maxterm 的数量最多为
思路: 先找出所有的组合.
两个变量, 则有 $2^2=4$ 种组合.
当 minterms 数量最多时有:
| A | B | C |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
则数量为 4.
当 maxterms 数量最多时有:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
则数量也为 4.
因此结论为, minterms 和 maxterms 的数量最多为 $2^n$
例3, 对于 $n=4$, 可能的 logic expression 为多少种
结论: 其数目为 $2^{2^n}$
这里 $n = 4$, 也就是说, 有 $2^{2^n} = 2^{2^4} = 65536$ 种可能
14 Positive and Negative Logic
Positive Logic
高电平对应 logic “1”
低电平对应 logic “0”
如:
“5V” $\rightarrow$ logic “1”
“0V” $\rightarrow$ logic “0”
Negative Logic
高电平对应 logic “0”
低电平对应 logic “1”
如:
“5V” $\rightarrow$ logic “0”
“0V” $\rightarrow$ logic “1”
15 对偶式 Dual Form
Dual Form, 也就是对偶式.
Positive logic AND gate
其真值表为:
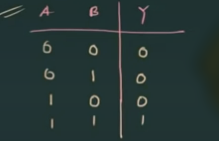
Negative logic AND gate
其真值表为:
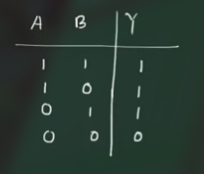
Positive logic OR gate
其真值表为:
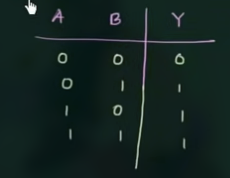
Negative logic OR gate
其真值表为:
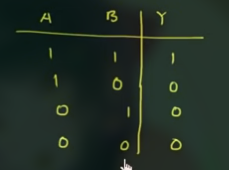
结论
对比四个 truth table 可知:
- Positive logic AND gate == Negative logic OR gate
- Negative logic AND gate == Positive logic OR gate
而 Dual Form 就是上述结论的应用, 将 Positive logic AND gate 转换为 Negative logic OR gate, 如:
$$
\displaylines
{
A \cdot B \overset{Dual}{\rightarrow} A + B
}
$$
注意, $A$ 并没有变为 $\overline{A}$, 这也是其和 complement 的区别.
16 自对偶 Self Dual
对于任意 logical expression 来说, 取两次对偶能得到同样的表达式. (也就是回到原来的式子)
如:
$$
\displaylines
{
F = AB\overline{C} + \overline{A}BC + ABC \newline~ \newline
F’ = (A+B+\overline{C}) (\overline{A}+B+C) (A+B+C) \newline~ \newline
F’’ = AB\overline{C} + \overline{A}BC + ABC
}
$$
对于 self dual expression 来说, 取一次对偶就能得到同样的表达式.
如:
$$
\displaylines
{
G = AB + BC + AC \newline~ \newline
G’ = (A+B) (B+C) (A+C) \newline~ \newline
= (B + AC) (A+C) \newline~ \newline
= AB + BC + AC \newline~ \newline
}
$$
这里的 $G = AB + BC + AC$ 就被称为 self dual expression.
一个结论
对于有 n 个变量的式子来说, 其对偶式共有多少种可能:
$$
\displaylines
{
2^{2^{n-1}}
}
$$
例, $Y = \overline{A} \overline{B} + \overline{B} \overline{C} + \overline{A} \overline{C}$ 是否为 self dual 式
$$
\displaylines
{
Y’ = (\overline{A} + \overline{B}) (\overline{B} + \overline{C}) (\overline{A} + \overline{C}) \newline~ \newline
= (\overline{A} + \overline{B}\overline{C}) (\overline{B} + \overline{C}) \newline~ \newline
= \overline{A}\overline{B} + \overline{A}\overline{C} + \overline{B}\overline{C}
}
$$
因此, 其是 self dual expression
例, $n = 4$ 的时候, 可能的 self dual 式的数量为多少
$$
\displaylines
{
2^{2^{4-1}} = 2^{2^{3}} = 2^8 = 256
}
$$
因此, 共有 256 种可能.
17 “补” 的含义 complement Meaning and Examples
如, 一个集合为 $U = \{a,e,i,o,u\}$, 其子集为 $A = \{a,e,i\}$, 那么其补集为 $\overline{A} = U - A = {o,u}$
对于 logic expression 来说, 总的集合为 $U = \{0,1\}$, 若 $A = {1}$, 那么其补集为 $\overline{A} = {0}$
18 维恩图 Venn Diagram
如:

19 开关电路 Switching Circuit
开关数 (若为 n) 和其 combination 的数量 (若为 m) 关系为:
$$
\displaylines
{
m = 2^n \newline~ \newline
n = \log_2 m
}
$$
注意 NAND (与非门) : $\overline{AB}$
其真值表和电路图如:
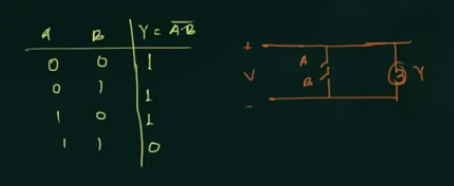
NOR (或非门) : $\overline{A + B}$
其真值表和电路图如:
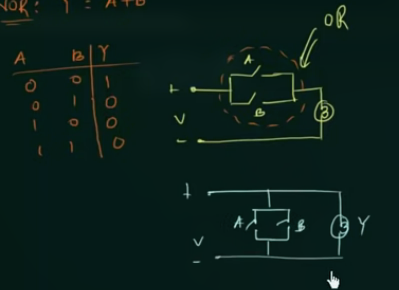
由电路图写出逻辑表达式, 如:
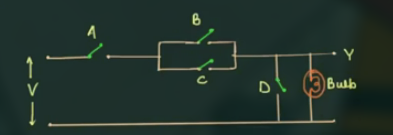
有:
$$
\displaylines
{
Y = A (B + C) \overset{D}
}
$$
(同样, 这里以使 bulb 基准, 需要联通的为 $A$ , 需要断开的为 $\overline{A}$)
20 Statement Problem
例1, 考虑一个逻辑电路, 其包含 3 个 inputs A,B,C, Output Y. 下列几种情况都使 Y 为 1 (high)
- B and C are true $BC$
- A and C are false $A’C’$
- A,B and C are true $ABC$
- A,B and C are false $A’B’C’$
(如第一个, 应该为, 只有当 B and C are true 时 Y 才为 1)
因此有:
$$
\displaylines
{
Y = BC + A’C’ + ABC + A’B’C’ \newline~ \newline
化简为: \newline~ \newline
Y = BC (1+A) + A’C’(1+B’) \newline~ \newline
= BC \cdot 1 + A’C’ \cdot 1 \newline~ \newline
= BC + A’C’
}
$$
例2, 找到函数 Y for the giving condition
- A 和 B are T
- A 和 C are T, B is F
- A is F, B 和 C are T
因此有:
$$
\displaylines
{
Y = AB + AB’C + A’BC \newline~ \newline
}
$$
例3, 一个逻辑电路有 3 个 inputs A,B & C. Output F 只有在 majority of inputs are logic 1 的时候为 high
- 化简 F
- 画出 logic circuit
其真值表为:

可以得到:
$$
\displaylines
{
F = A’BC + AB’C + ABC’ + ABC \newline~ \newline
最终化简为: \newline~ \newline
F = AB + AC + BC
}
$$
(不知道为什么是写 SOP Form)
从 F 的表达式可知, 需要:
- 1 OR (3 个并联)
- 3 AND
则 logic circuit 为:
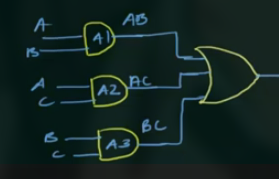
21 数字系统 Number Systems
数字系统定义了一组用于表示数量的值, 数字系统定义了一组用于呈现数量的值
如:

示例:
$$
\displaylines
{
(7392)_{10} = 7000 + 300 + 90 + 2 \newline~ \newline
= 7 \times 10^3 + 3 \times 10^2 + 9 \times 10^1 + 2 \times 10^0
}
$$
数字系统分为 :
- weighted: Decimal, Binary, Octal, BCD, etc
- unweighted: Gray code, etc
一个结论:
- 提高 base, 则位数减少
如:
$$
\displaylines
{
(1110011100000)2 \rightarrow (7392){10}
}
$$
22 二进制数字系统 Binary Number System
由 $0 \sim (r-1),\ r=2$ 可知, 对于二进制而言, 每一位只可能为 0 或 $2-1$ (即1).
一个例子:
$$
\displaylines
{
(10101.11)_2 = 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 1 \times 2{-1} + 1 \times 2^{-2}
}
$$
两个概念 :
- MSB (Most Significant Bit, 因为权重最大):
- LSB (Least Significant Bit, 因为权重最小):
如:
Bit 是最小的单位, 一般有:
- 1 Nibble = 4 bits
- 1 Byte = 8 bits
- 1 word = 16 bits = 2 bytes
- 1 double = 32 bits = 4 bytes
23 二进制乘法 Binary Multiplication
和十进制乘法相同.
如 $1010$ 和 $101$ 相乘, 可以转换为:

或者更简单的写法:

24 二进制除法 Binary Division
和十进制除法相同.

25 r’s Complement
Complement 一般分为两种:
- r’s complement (Radix complement)
- (r-1)’s complement (Diminised Radix complement)
例子
$(7)_{10}$ 的 complement (也就是求 1 位 10 进制的 complement)
$$
\displaylines
{
(7)_{10} = 10 - 7 = 3
}
$$
同样:
$$
\displaylines
{
(9)_{10} = 10 - 9 = 1 \newline~ \newline
}
$$
有这样的结论, $N$ 是用于求补的数 (如这里的 7), $n$ 为位数 (如这里是 1 位), $r$ 是基数, 则有:
$$
\displaylines
{
r’s\ complement = r^n - N
}
$$
例1, $N = 5690$, 求 10’s complement
则有:
$$
\displaylines
{
10’s\ complement = 2^4 - 5690 \newline~ \newline
= 4310
}
$$
例2, $N = 1101$, 找到 2’s complement
有:
$$
\displaylines
{
2’s\ complement = 2^4 - 1101 \newline~ \newline
= 10000 - 1101 \newline~ \newline
= 1111 + 1 - 1101 \newline~ \newline
= 0011
}
$$
例3, $N = 76895$, 求 10’s complement
$$
\displaylines
{
10’s\ complement = 10^5 - 76895 \newline~ \newline
= 23105
}
$$
例4, $N = 11011$, 求 2’s complement
$$
\displaylines
{
2’s\ complement = 2^5 - 11011 \newline~ \newline
= 100000 - 11011 \newline~ \newline
= 00101
}
$$
26 (r-1)’s Complement
如:
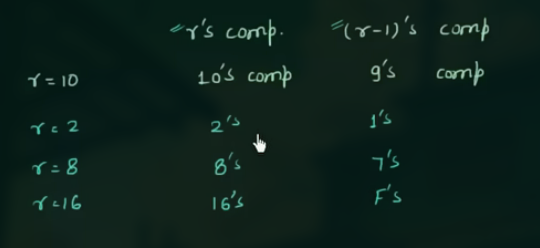
这里, 是利用 (r-1)'s complement 来计算 r's complement.
其关系为:
$$
\displaylines
{
(r-1)’s\ complement = r’s complement - 1
}
$$
如 (这里以 5526 的 10’s complement 为例):
$$
\displaylines
{
10’s complement = 10^4 - 5526 \newline~ \newline
9’s complement = 9999 - 5526
}
$$
( 疑问 , 为什么 10’s complement 是 $10^n - N$, 而 9’s complment 是 $9..9 - N$ )
27 1’s & 2’s Complement 的例子
例1, 得到 $(1010)_2$ 的 1’s complement
$$
\displaylines
{
1111 - 1010 = 0101
}
$$
例2, 得到 $(10111010)_2$ 的 2’s complement
$$
\displaylines
{
11111111 - 10111010 + 1 = 01000101
}
$$
28 得到 2’s complement 的简化方法
分为 4 步:
- 写下 given number
- 从 LSB 开始, copy 所有 0 直到遇到第一个 1
- copy 第一个 1
- Complement 其他剩下的 bits
如, 求 $10111000$ 的 2’s complement:
$$
\displaylines
{
10111000 \newline~ \newline
01001000
}
$$
29 二进制中用 Signed Magnitude 表示数据
二进制中表示一个数据的方法有:
- Magnitude
- Unsigned (只表示正数)
- Signed (表示正数和负数)
- Complement
- 1’s Complement (表示正数和负数)
- 2’s Complement (表示正数和负数)
在这四种表述方式中, 正数的表示形式都是一样的.
对于 signed magnitude:
其范围为:
$$
\displaylines
{
-(2^{n-1} - 1) \sim (2^{n-1} - 1)
}
$$
其表示 $\pm 6$ 为:
$$
\displaylines
{
+6 = 0110 \newline~ \newline
-6 = 1110
}
$$
(只改变了符号位)
对于 1’s complement
其范围为:
$$
\displaylines
{
-(2^{n-1} - 1) \sim (2^{n-1} - 1)
}
$$
其表示 $\pm 6$ 为:
$$
\displaylines
{
+6 = 0110 \newline~ \newline
-6 = 1001
}
$$
(按位取反)
这种表示方法会有一个问题, 就是:
$$
\displaylines
{
+0 = 0000 \newline~ \newline
-0 = 1111
}
$$
对于 2’s complement
其范围为:
$$
\displaylines
{
-2^{n-1} \sim 2^{n-1} - 1
}
$$
其表示 $\pm 6$ 为:
$$
\displaylines
{
+6 = 0110 \newline~ \newline
-6 = 10000 - 0110 \newline~ \newline
= 1111 - 0110 + 1 \newline~ \newline
= 1010
}
$$
2’s complement 中, 最高位同样表示符号位.
对 1 个 负数取 2’s complement 可以得到其正数形式.
30 Binary Subtraction using 1’s Complement
计算机中的减法是基于加法来计算的:
$$
\displaylines
{
A - B = A + (-B)
}
$$
因此需要将 B 转换为其负数形式, 这里用 1’s complement 表示负数, 则计算步骤为:
- 将 B 转换为 1’s complement
- 进行 $A+(-B)$
- 如果 final carry 为 1, 那么将其 add to the result obtained in step 2. 如果 final carry 为 0, 那么 result obtained in step 2 is negative and in the 1’s complement form, (可以再取一次 1’s complement 计算其是多少的负数)
例1 计算 $(1100)_2 - (0101)_2$
$$
\displaylines
{
A = 1100 \newline~ \newline
B = 0101 \newline~ \newline
-B = 1010 \newline~ \newline
A + (-B) = 1100 + 1010 \newline~ \newline
= 0110,\ carry = 1 \newline~ \newline
result = 0110 + 1 = 0111
}
$$
例2 计算 $(0101)_2 - (1100)_2$
$$
\displaylines
{
A = 0101 \newline~ \newline
B = 1100 \newline~ \newline
-B = 0011 \newline~ \newline
A + (-B) = 0101 + 0011 \newline~ \newline
= 1000,\ carry = 0 \newline~ \newline
}
$$
由于 $carry=0$, 表明其是负数, 由其 1’s complement 可知其正数为 $0111$, 因此其为 $-7$
31 Binary Subtraction using 2’s Complement
也就是利用 2’s complment 来完成二进制减法.
同样, 将 $A - B$ 视为 $A + (-B)$ 进行计算, 但这里的 $-B$ 是用 2’s complment 来表示.
其分为三个步骤:
- 找到被减数的 2’s complement 形式
- 进行加法
- 如果 final carry 为 1, 那么结果为正数, 且为正常二进制形式; 如果 final carry 为 0, 那么其结果为负数, 且为 2’s complement 形式
对于 2’s complement 而言, final carry 一般都会被忽略. (不会像 1’s complement 那样往回加)
例子, $(1001)_2 - (0100)_2$
$$
\displaylines
{
A = 1001 \newline~ \newline
B = 0100 \newline~ \newline
-B = 1111 - 0100 + 1 = 1100 \newline~ \newline
A + (-B) = 1001 + 1100 = 0101,\ carry = 1
}
$$
判断 overflow 的条件 (一个 trick)
假设 x 和 y 是两个数的 sign bit, z 是结果的 sign bit, 若:
$$
\displaylines
{
\overline{x} \overline{y} z + x y \overline{z} = 0
}
$$
则没有溢出.
若:
$$
\displaylines
{
\overline{x} \overline{y} z + x y \overline{z} = 1
}
$$
则溢出.
(也就是说, 两个正数相加为负数则溢出, 两个负数相加为正数也为溢出)
32 编码的分类 Classification of Codes
简单来说, 编码是 a group of simbels.
其分为 6 种:
- Weighted Codes (编码的每一位有权重)
- Binary
- 8421 码
- 2421 码
- Non-Weighted Codes (编码的每一位都没有权重)
- XS-3
- Gray
- Reflective Codes (也被称为 self complementing code, 对于其表示的码来说, 如 2421 码, 其特点为: 9 (1111) 的补为 0 (0000), 8 (1110) 的补为 1 (0001), 7 (1101) 的补为 2 (0010) 等)
- 2421
- XS-3
- Sequential Codes
- 8421 码
- XS-3
- Alphanumeric Codes
- ASCII
- Error Detecting & Correcting Codes
- Hamming code
2421 码的例子
2421 对应四位上的权重.
其补码的特点:

33 Binary Coded Decimal (BCD) Code
BCD 码就是用 4 位二进制来表示一个十进制 digit. 这 4 位的权重分别为 8-4-2-1 (因此也称为 8421 码)
其标识 0 ~ 9 为:

因为是 4 位, 原本可以表示 16 个数, 但这里只用了 10 个, 因此有 6 个 BCD 码是无效的.
将十进制转换为 BCD
$$
\displaylines
{
(17)_{10} \rightarrow 0001\ 0111
}
$$
将 BCD 转换为十进制
$$
\displaylines
{
10100 \rightarrow 00010100 \newline~ \newline
\rightarrow 0001\ 0100 \newline~ \newline
\rightarrow 14
}
$$
BCD 码的效率比 Binary 低, 因为其用到更多位数.
34 BCD Addition
对 BCD 码做加法, 只需要按照 Binary 的加法即可, 但需要注意:
- 当 $Sum \le 9, Final\ Carry = 0$ 时, Answer is correct
- 当 $Sum \le 9, Final\ Carry = 1$ 时, Answer is incorrect, 需要加上 (0110) 来修正
- 当 $Sum > 9, Final\ Carry = 0$ 时, Answer is incorrect, 需要加上 (0110) 来修正
(这里和 9 做比较的原因为, BCD 码只用于表示 $0 \sim 9$)
例1, 用 BCD 码表示 $2_{10} + (6)_{10}$
其相加结果为 $8<9$
$$
\displaylines
{
2_{10} = 0010 \newline~ \newline
(6)_{10} = 0110 \newline~ \newline
0010 + 0110 = 1000
}
$$
此时, 结果小于 9, 且 $carry = 0$, 因此结果正确
例2, 用 BCD 码表示 $3_{10} + (7)_{10}$
其相加结果为 $10>9$
$$
\displaylines
{
3_{10} = 0011 \newline~ \newline
(7)_{10} = 0111 \newline~ \newline
0011 + 0111 = 1010
}
$$
由于 carry = 0, 因此需要加上 $0110$, 也就有:
$$
\displaylines
{
1010 + 0110 = 10000
}
$$
此时才为用 BCD 码正确表示 10.
例3, 用 BCD 码表示 $8_{10} + (9)_{10}$
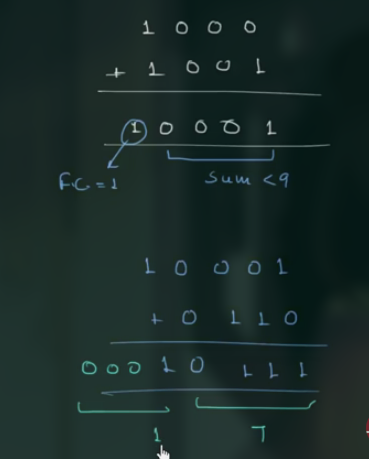
另一个重要例子

35 Shift Add-3 Method
这个方法用于将 Binary 转换为 BCD.
如, 15 用二进制表示为 1111, 用 BCD 码表示为 0001 0101, 而这个方法, 就是将 1111 转化为 0001 0101.
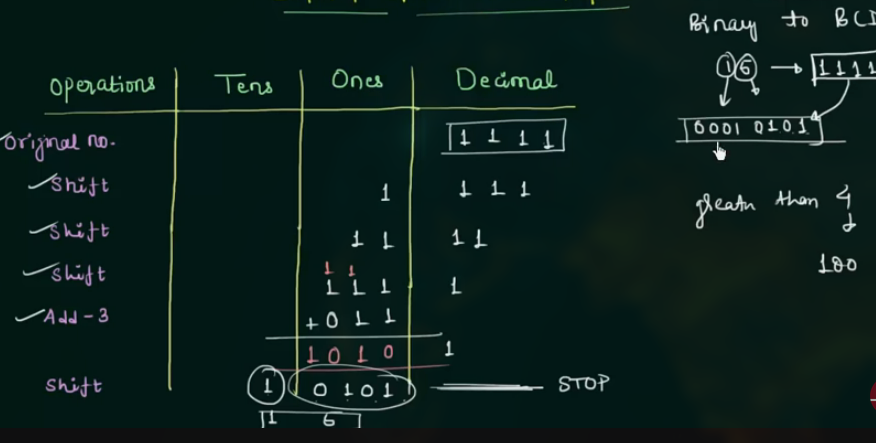
(感觉不是很方便)
36 2421 码
也是一种 BCD 码, 其 4 位的权重分别为 2-4-2-1, 且具有 self complement 的特点.
其他集中 BCD 码有:

37 余3码 Excess-3 Code
其就是 8-4-2-1 码加上 0011 的结果:

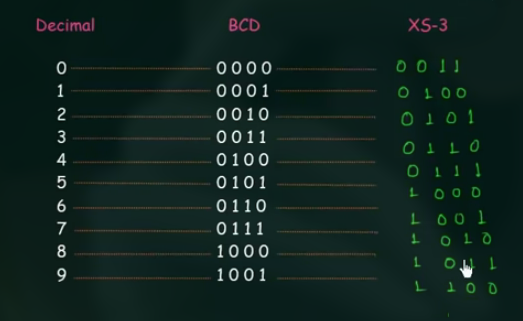
因此, XS-3 码也是 unweighted code.
由上图可知, 其同样为 self complement 的.
有一个重要观点: XS-3 codee 是 unweighted code 中唯一的 self complement code
一个判断一种 weighted 编码是否 self complement 的小 trick
将 wight 相加, 看是否为 9, 若值为 9, 则是 self complement, 若不为, 则不是.
如:
2-4-2-1, 有 $2 + 4 + 2 + 1 = 9$, 因此其为 self complement
8-4-2-1, 有 $8 + 4 + 2 + 1 = 15$, 因此其不为 self complement.
unweighted 则不用判断, 因为只有 XS-3 code 是 self complement.
38 余三码加法 Excess-3 Code Addition
求两个十进制数的和的余三码.
需要注意, 这里不能直接将两个十进制数的余三码相加, 因为这样会 excess-6 而不是 3.
如:

这里要注意, $carry = 0$ 时要减去 $0011$, 因为此时 excess-6; $carry = 1$ 是要加上 $0011$ (原因不知)
39 格雷码 Gray Code
Gray code, 也称为10中取1码, 二进制反射码 (Reflected Binary Code) .
格雷码是无权重码, 每一个位没有权重.
格雷码中的相邻码值, 只有一位改变:

这里, 看 3 和 4 的格雷码, 只有 1 位发生了改变. 而 3, 4 的二进制码改变了 3 位.
二进制码转换为格雷码 , 步骤为:
- 记录最高位
- 将最高位和 the next bit 相加, 记录结果 (做 XOR 运算)
- 重复步骤
如:
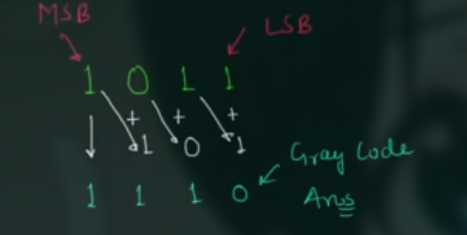
感觉就是错位相加, 如将 1110 转换为格雷码:
$$
\displaylines
{
1110 \newline~ \newline
+1110 \newline~ \newline
=001 \newline~ \newline
最终为: \newline~ \newline
1001
}
$$
(其实这里也就是上一位和下一位做 XOR 运算)
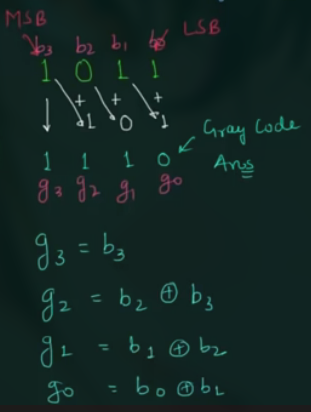
( $\oplus$ 表示 XOR 运算 )
40 将格雷码转为二进制 Gray Code to Binary Conversion
分为 3 步:
- 记录 MSB
- 将二进制数的最高位和格雷码的 the next bit 相加, 记录结果 (做 XOR 运算)
- 重复步骤.
如:
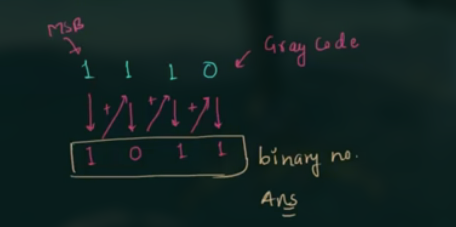
也有:

41 什么是奇偶校验 What is Parity
其用于检测错误.
单个 奇偶校验位 (parity bit) (指只添加一个比特位)
例如, 要发送 d 比特信息.
偶校验方案, 附加一个比特, 使得 d + 1 比特中 1 的总数是 偶数.
奇校验方案, 附加一个比特, 使得 d + 1 比特中 1 的总数是 奇数.

接收方 需要数接受比特中 1 的数目.
这种方式容易未检出差错, 比如偶校验方案中有偶数个比特发生差错就检测不出.
更健壮的差错检测方案 , 二维奇偶检验 (two-dimensional parity), 将 d 个比特划分为 i 行 j 列, 对每行每列计算奇偶值:
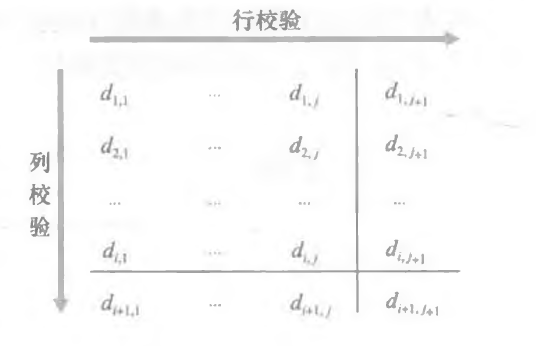
利用类似于坐标的形式对错误进行纠正:
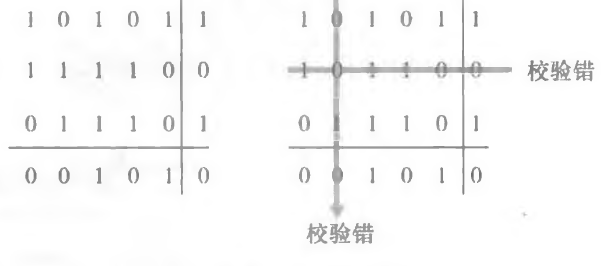
接收方检测和纠正差错的能力被称为 向前纠错 (Forward Error Correction, FEC)
42 Hamming Code - Error Detection
Hamming Code 是由 R.W.Hamming 发明的.
最常见的是 7-bit Hamming code. 其包含:
- 4 位 Data bits
- 3 位 Parity bits
在 R.W.Hamming 的规则中, 放置 Parity bits 的位置满足 $2^n,\ n=0,1,…,n$.
如, 放在 $2^0=1$ 第1位, $2^1=2$ 第2位, $2^2=4$ 第4位 (由于这里一共 7 位, 没有第8位, 因此只有 3 位 Parity bits). 其他位放 Data bits.
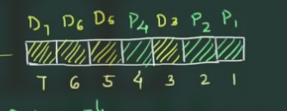
这里, Parity bits 和 Data bits 的关系为:
$$
\displaylines
{
P_1 \rightarrow D_3 D_5 D_7 \newline~ \newline
P_2 \rightarrow D_3 D_4 D_7 \newline~ \newline
P_4 \rightarrow D_5 D_6 D_7
}
$$
(这里的 Parity bit 的下标是其位置)
注意, 这里不是 AND 运算, 而是观察 1 的个数是 odd 还是 even.
如, 数据位为:
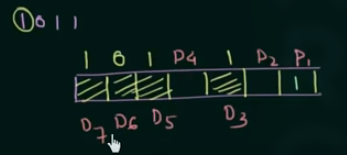
那么可以得到 Parity bits 为:
$$
\displaylines
{
P_1 = 1 (111 有 3 个 1)\newline~ \newline
P_2 = 0 (101 有 2 个 1)\newline~ \newline
P_4 = 0 (101 有 2 个 1)
}
$$
43 逻辑门 Logic Gates
逻辑门是用来表现逻辑操作的物理器件, 可以有 1 个或多个逻辑输入, 然后产生一个逻辑输出.
Basic Gates: NOT, AND & OR (因为这三个能组合出任意的电路)
Universal Gates: NAND & NOR (因为, 只用 NAND 或 NOR 可以表现任意的 Digital system)
Arithmatic Gates: XOR & XNOR (因为用这两个门处理运算)
NOT Gate
有两种画法:
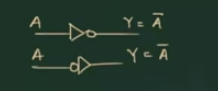
(也就是在箭头前或后加一个圈)
Truth table 就是所有 input/output 的可能的组合.
NOT Gate 的真值表为:
| A | $Y = \overline{A}$ |
|---|---|
| 0 | 1 |
| 1 | 0 |
对于一个 Buffer 而言, 输入等于输出:
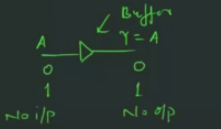
例题, 下列电路中, 每一个 NOT gate 的 propagation delay 为 100 psec. 则其生成波形的频率为

其周期可得: 1ns, 则频率为 $\frac{1}{1 \times 10^{-6}} = 10^6$
从这里可知, NOT Gate 可以用来生成方波. 也就用上述的电路.
AND Gate
AND Gate 用于 AND Operation, 也就是, 只有 input 都为 high 时, output 才为 high.
其符号为:
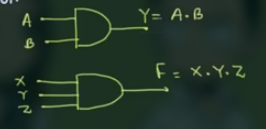
其 truth table 为:
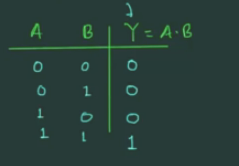
其满足结合律和交换律:
$$
\displaylines
{
A \cdot (B \cdot C) = (A \cdot B) \cdot C \newline~ \newline
A \cdot B = B \cdot A
}
$$
AND Gate 的 enable 和 disable 作用.

disable: 下面的输入如果是 0, 那么无论 A 是什么输入, 输出都是 0.
enable: 下面的输入如果是 1, 那么 A 是什么输入, Y 的输出都是 A.
在 TTL logic (Transistor-Transistor Logic) 中, 如果某个 input 处于 open 或 floating 状态, 将其视为 “1”.
而在 ECL logic (Emitter-Coupled Logic) 中, 将其视为 “0”.
OR Gate
OR Gate 用于进行 OR 运算, 即, 只要有一个 input 为 high, 那么 output 则为 high.
其符号为:
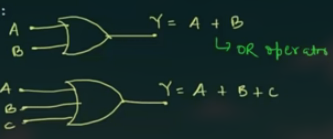
其真值表为:

其同样满足交换律和结合律.
enable: 对于两个 inputs 的 OR Gate 来说, 一个 input 为 “0”, 则 output 和另一个 input 相同 (也就是作为一个 buffer)

disable: 而当一个 input 为 “1” 时, 则另一个 input 失去作用, 此时的输出总为 1:

OR Gate 在 TTL 中, unused/floating input 被视为 “1”.
OR Gate 在 ECL 中, unused/floating input 被视为 “0”.
NAND Gate 和 NOR Gate
这两个 Gates 都是由 basic gates 得来.
NAND Gate 有两种构建方法, 为:
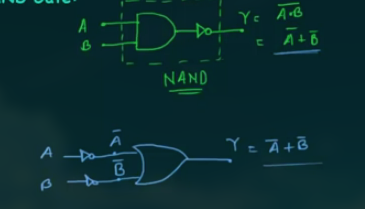
其符号也有两种:

(因此 NAND Gate 也称为 Bubbled OR)
NOR Gate 也有两种构建方法:
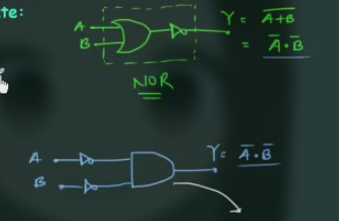
其符号也为两种:
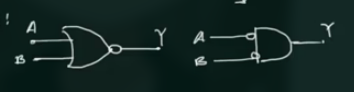
(因此 NOR Gate 也称为 Bubbled AND)
这两个逻辑门 不满足结合律 , 但其满足交换律.
Exclusive OR Gate (XOR)
其符号为:
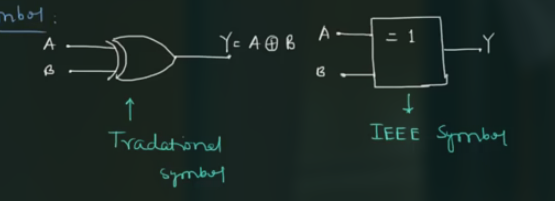
其内部电路为:
$$
\displaylines
{
Y = A \oplus B \newline~ \newline
= A \overline{B} + \overline{A} B \newline~ \newline
= (A+B) (\overline{A} + \overline{B})
}
$$
(两种形式)
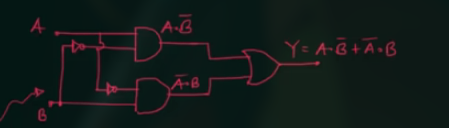
其逻辑表达式为:
其真值表为:

其有一个叫 odd 1’s detector 的特性. (也就是遇到奇数个 1 输出才为 high)
其 enable 和 disable 特性:
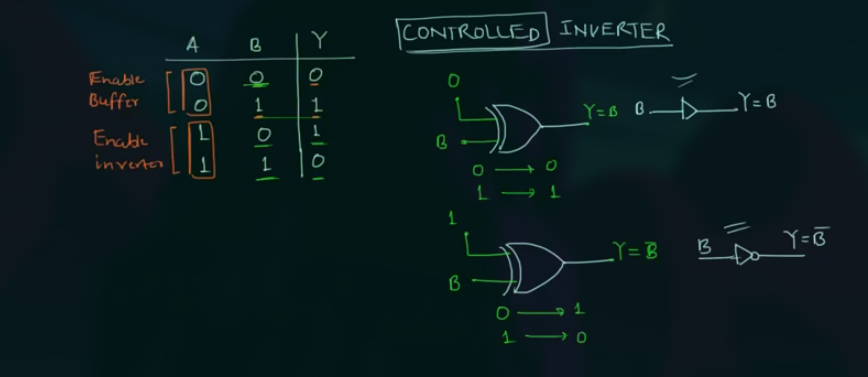
当 A 为 0 时, 其工作为 buffer.
当 A 为 1 时, 其工作为 invertor.
特性
1.
$$
\displaylines
{
A \oplus A = 0 \newline~ \newline
A \oplus \overline{A} = 1 \newline~ \newline
A \oplus 0 = A \newline~ \newline
A \oplus 1 = \overline{A} \newline~ \newline
}
$$
2.
$$
\displaylines
{
if \newline~ \newline
A \oplus B = C \newline~ \newline
then \newline~ \newline
B \oplus C = A \newline~ \newline
A \oplus C = B \newline~ \newline
A \oplus B \oplus C = 0 \newline~ \newline
}
$$
3.
$$
\displaylines
{
A \oplus A = 0 \newline~ \newline
A \oplus A \oplus A = A \newline~ \newline
A \oplus A \oplus A … \oplus A \newline~ \newline
(其结果取决于 A 的个数)
A \oplus A \oplus A … \oplus A = A, \ n = odd\newline~ \newline
A \oplus A \oplus A … \oplus A = 0, \ n = even\newline~ \newline
}
$$
例题, 20 个 XOR Gate 级联, 求 output
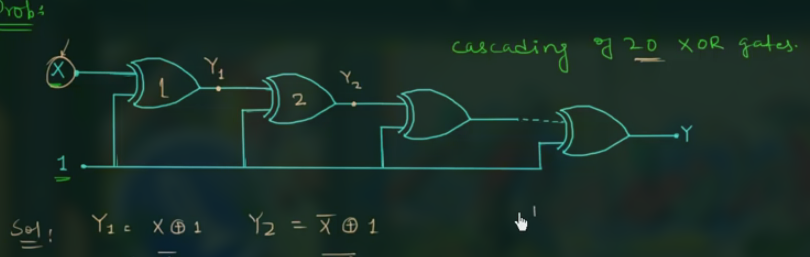
$$
\displaylines
{
Y_1 = X \oplus 1 = \overline{x} \newline~ \newline
Y_2 = \overline{x} \oplus 1 = x \newline~ \newline
…
Y = x
}
$$
XNOR Gate
其就是 XOR 加上一个 NOT, 电路图为:
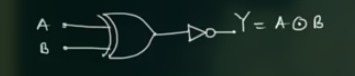
其符号为;
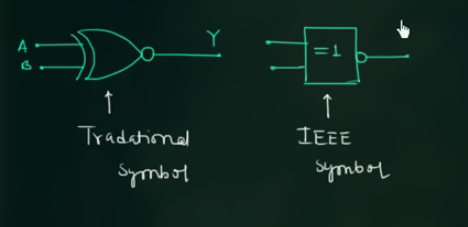
逻辑表达式为:
$$
\displaylines
{
Y = A \odot B = A \cdot B + \overline{A} \cdot \overline{B}
}
$$
其真值表为:
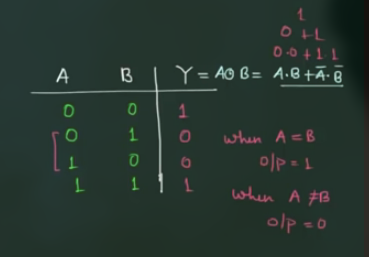
其满足交换律和结合律.
enable 和 disable 特性:
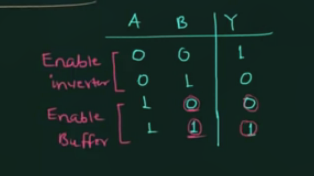
(即, A 为 0 时, 其工作为 invertor; A 为 1 时, 其工作为 Buffer.)
性质 :
1.
$$
\displaylines
{
A \odot A = 1 \newline~ \newline
A \odot \overline{A} = 0 \newline~ \newline
A \odot 0 = \overline{A} \newline~ \newline
A \odot 1 = A
}
$$
2.
$$
\displaylines
{
A \odot A \odot A … \odot A = A,\ n=odd \newline~ \newline
A \odot A \odot A … \odot A = 1,\ n=even \newline~ \newline
(n 表示 A 的个数)
}
$$
3.
当有 even 个数的 input 时, XOR 和 XNOR 互补.
当有 odd 个数的 input 时, XOR 和 XNOR 相同.
如:
$$
\displaylines
{
A \oplus B \oplus C = A \odot B \odot C \newline~ \newline
(此时为 3 个 input, 即 odd)
A \oplus B \oplus C \oplus D = \overline{A \odot B \odot C \odot D} \newline~ \newline
(此时为 4 个 input, 即 even)
}
$$
44 NAND as Universal Gate
AND, OR 和 NOT 能够组成任意 digital system.
NAND 或者 NOR 能够转换为 AND, OR 和 NOT, 因此任意 digital system 也能仅由 NAND 或 NOR 组成.
NAND as NOT
NAND 为 $Y = \overline{AB}$
NOT 为 $Y = \overline{A}$
因此当 $B=A$ 时, $\overline{AB} = \overline{AA} = \overline{A}$, 此时 NAND as NOT
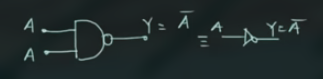
此处, 需要 1 个 NAND
NAND as AND
给 NAND Gate 加上用 NAND Gate 表示的 NOT Gate 就能作为 AND 使用:
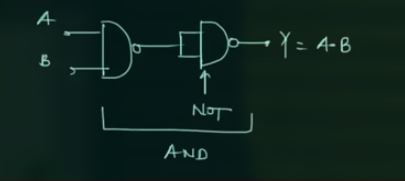
此处, 需要 2 个 NAND
NAND as OR
NAND 为 $Y = \overline{AB} - \overline{A} + \overline{B}$
因此, 只用:
$$
\displaylines
{
A \rightarrow \overline{A} \newline~ \newline
B \rightarrow \overline{B}
}
$$
即可.
同样, 加上用 NAND 来表示的 NOT:
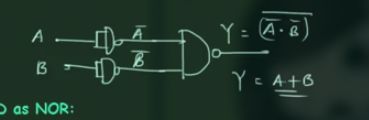
此处, 需要 3 个 NAND
NAND as NOR
需要 NAND 表示的 OR 和 NOT:
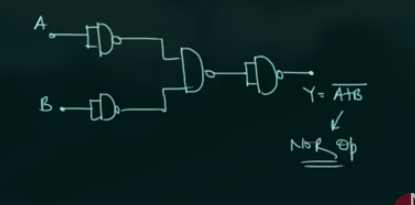
此处, 需要 4 个 NAND
NAND as EXOR
EXOR 为 $Y = A \overline{B} + \overline{A} B$
此处需要:
- 2 NOT
- 2 AND
- 1 OR
由于 Basic gates 都能由 NAND 表示了, 因此:
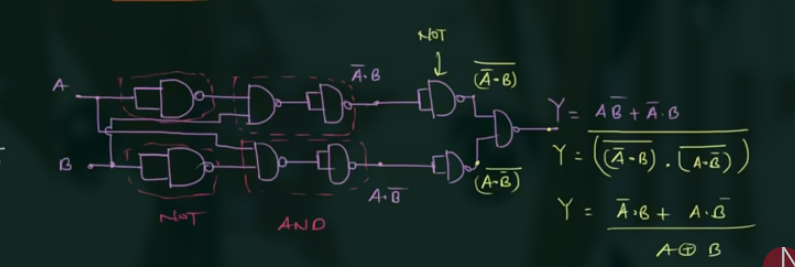
此时不是最简化的. 可以仅用 4 个 NAND 表示.
即:
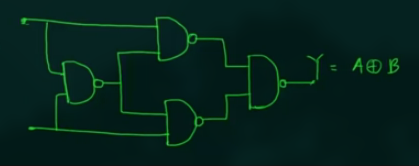
NAND as EXNOR
也就是给 NAND 表示的 EXOR 加上一个 NOT.
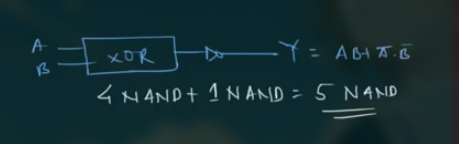
45 NOR as Universal Gate
NOR as NOT
NOR 为 $Y = \overline{A + B}$
NOT 为 $Y = \overline{A}$
因此只要 $A = B$, 则有 $Y = \overline{A + B} = \overline{A + B} = \overline{A}$
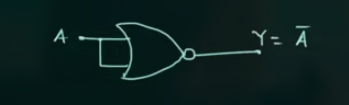
此处, 用了 1 个 NOR Gates
NOR as OR
也就是给 NOR 加上 NOR 表示的 NOT.
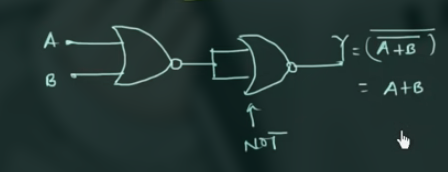
此处, 用了 2 个 NOR Gates
NOR as AND
NOR 有: $Y = \overline{A + B} = \overline{A} \overline{B}$
AND 为: $Y = AB$
因此, 若要表示 AND, 则只需要:
$$
\displaylines
{
A \rightarrow \overline{A} \newline~ \newline
B \rightarrow \overline{B}
}
$$
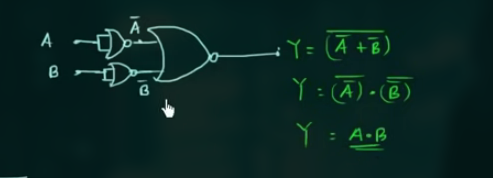
此处, 用了 3 个 NOR Gates
NOR as NAND
只用将 NOR 表示的 AND 加上一个 NOR 表示的 NOT:
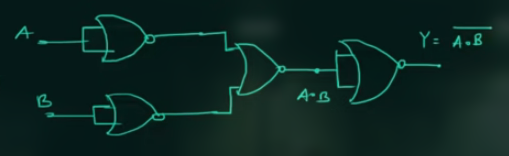
此处, 用了 4 个 NOR Gates
NOR as XOR
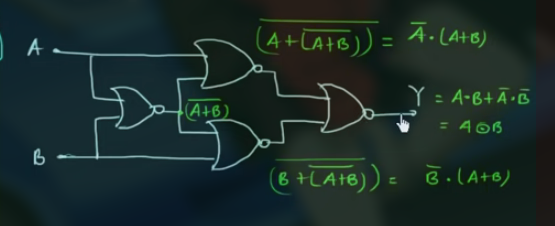
此处, 用了 4 个 NOR Gates
NOR as XNOR
给 NOR 表示的 XOR 加上 1 个 NOT.
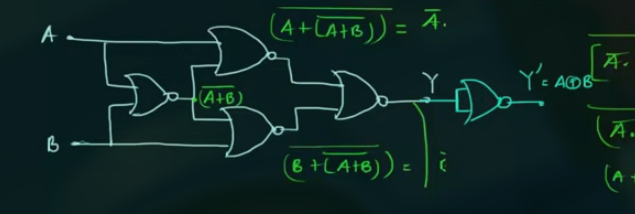
此处, 用了 5 个 NOR Gates
45 Karnaugh Map
Karnaugh Map 可以简写为 K’Map
Karnaugh map(K-map)是一种在数字逻辑和电路设计中用于简化布尔表达式的工具。它是由美国数学家Maurice Karnaugh于1953年发明的。
K-map的主要作用是通过可视化的方式展示布尔函数的真值表,并提供了一种方法来优化布尔表达式。通过对相邻的1进行分组,可以将布尔表达式简化为更简单的形式,从而减少逻辑门的数量和延迟,并提高电路的性能和可靠性。
K’Map 的结果就是 最简的逻辑表达式 (minimal logic expression)
如, 用一个布尔表达式, 画出其真值表:

( 总的组合数, 这里为 8 种, 因为有 3 个变量, 每个变量有 2 个值, 因此总的有 $2^3$ 种组合 )
由这个真值表, 可以得到 Canonical SOP Form, 即:
$$
\displaylines
{
F = \overline{A}B\overline{C} + A\overline{B}\overline{C} + A\overline{B}C + AB\overline{C} + ABC
}
$$
利用直接的逻辑表达式化简方法, 能够最终得到最简式 $F = A + B\overline{C}$, 但很麻烦.
使用 K’map 的方法:
首先写出所有的 cells:
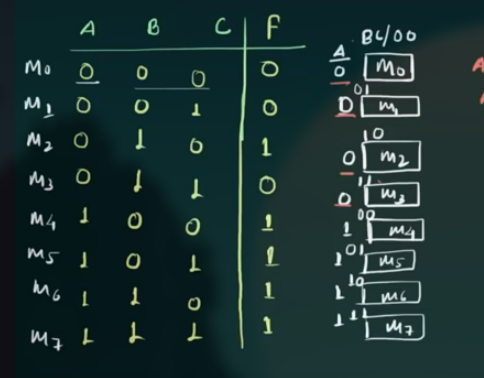
(也就是右侧白色部分)
重排这些 cells, 使得相邻两个 cells 的组合只有一个变量的值发生改变:
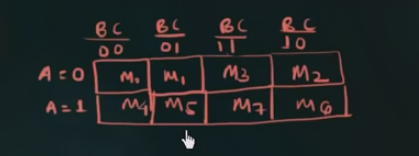
(cell 里面填的是 minterm, 上述的组合中只有一个变量的值发生变化也就是, minterm 中有一位发生变化)
这样安排的最主要原因为, 应用 $A + \overline{A} = 1$ 的性质.
注意, 这也算相邻:
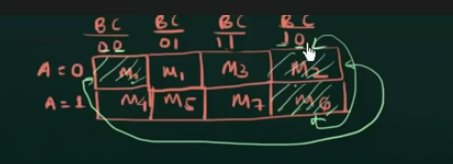
(同样满足只有 1 位改变)
这也被称为map rolling
对于画出 3 变量的 K’Map, 可以首先画出:
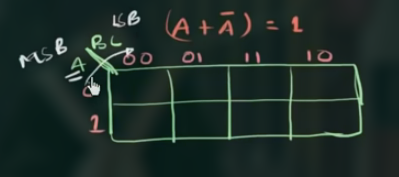
注意 MSB 和 LSB 的位置.
然后填入真值表的结果:
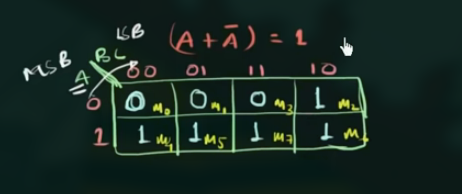
需要注意 $m_2,m_3$ 以及 $m_6,m_7$ 放置的位置.
下一步 是进行配对 (pairing), 只对周围有 2 个 1, 4 个 1, 8 个 1 … (2 的倍数个 1) 的进行配对. 单个 1 可以单独圈出.
在画圈时, 不能沿对角线.
如, 圈出 4 个 1:
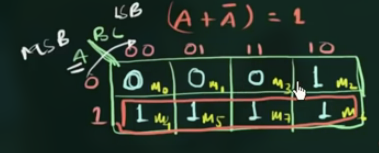
(圈出的, 实际上就是一个 minterm)
最终为:
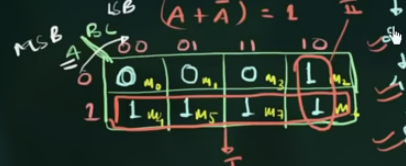
注意, “圈” 需最大, 且最少.
可以由这个 “圈” 写出最简的 SOP, “圈” 中值发生改变的变量写为 “1”, 未改变就写为如 “A” 或 “$\overline{A}$” (根据表格上的数字来写):
变化的量写为 1 的原因 , 变化的量就是 $A+\overline{A}=1$
$$
\displaylines
{
F = A \cdot 1 \cdot 1 + 1 \cdot B \overline{C}
}
$$
解释, 为什么说利用了 $A + \overline{A} = 1$
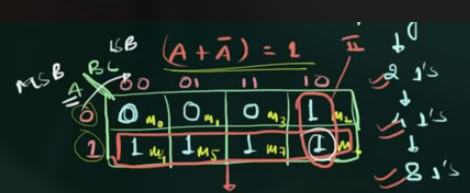
对于 II 而言 (右边那个圈), 可以写为:
$$
\displaylines
{
\overline{A} B \overline{C} + AB \overline{C} \newline~ \newline
= B\overline{C}(A + \overline{A}) \newline~ \newline
= B\overline{C}
}
$$
也就是圈出来化简的结果.
例1
已知有:
$$
\displaylines
{
f(A,B,C) = \sum m (1,3,5,7) \newline~ \newline
(A 为 MSB, C 为 LSB)
}
$$
步骤:
找到变量的数量. 这里为 3 个 $n = 3$(A,B,C).
找到 K’Map 中需要的 cells 数量 (也就是truth table 的所有组合数). 这里为 $2^3 = 8$
画出 K’Map 的框架
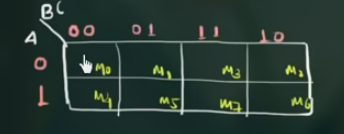
- 填好 K’Map
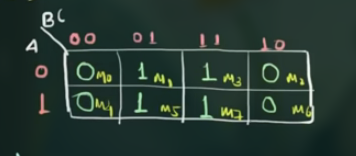
- 圈出 1, 并写出结果
$$
\displaylines
{
Y = 1 \cdot 1 \cdot C = C
}
$$
例2
已知有:
$$
\displaylines
{
F(A,B,C) = \sum m (0,1,2,4,7)
}
$$
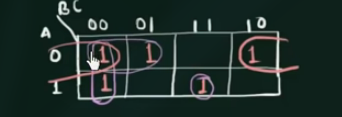
得:
$$
\displaylines
{
F = 1 \cdot \overline{B} \overline{C} + \overline{A} \overline{B} \cdot 1 + \overline{A} \cdot 1 \cdot \overline{C} \newline~ \newline
= \overline{BC} + \overline{AB}+ ABC + \overline{AC}
}
$$
例3
若有:
$$
\displaylines
{
F(A,B,C) = \sum m (1,3,6,7)
}
$$
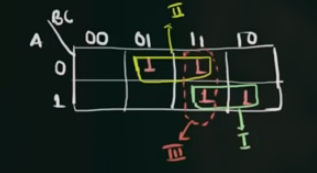
有:
$$
\displaylines
{
F = AB + \overline{A}C + BC
}
$$
实际上, 中间的 “圈” 可以被省略.
因为最简形式应该为 (由 Redundancy theory 可得):
$$
\displaylines
{
F = AB + \overline{A}C
}
$$
例4
有:
$$
\displaylines
{
F(A,B,C) = \sum m (0,1,5,6,7)
}
$$
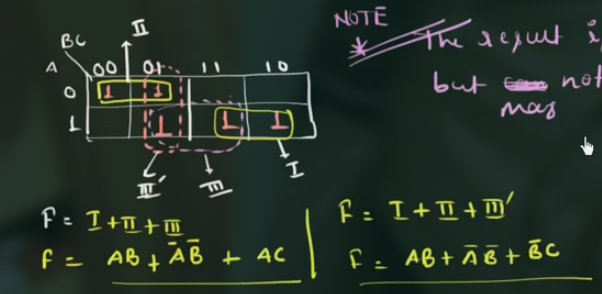
重要结论, k’map 的结果是最简式, 但其结果不唯一. (由上面的例子可知)
46 K’Map and Implicants
The group of 1’s is called an implicants (也就是 K’Map 中对 “1” 进行的分组)
Prime Implicants 指最大的 1’s group.
Essiential Prime Implicants, 也是最大的 1’s group, 但其包含至少一个 single 1, 其不能和其他 “1” 组合
16 cells 的 K’Map:

47 4 Variable Karnaugh Map
例1
$$
\displaylines
{
f(A,B,C,D) = \sum m (0,2,3,7,11,13,14,15)
}
$$
(A 为 MSB, D 为 LSB)
由于是 4 变量, 因此是 16 个 cells.
注意, minterm 的放置位置.
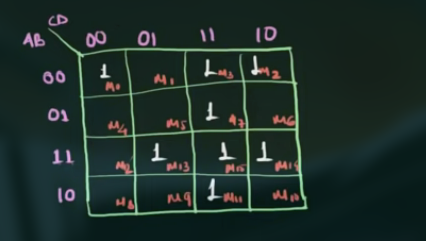
combination 的方式:
则有:
$$
\displaylines
{
F = CD + \overline{ABD} + ABC + ABD
}
$$
例2
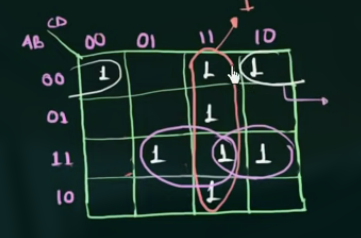
已知: $F(A,B,C,D) = \sum m(0,2,3,5,7,8,10,11,14,15)$
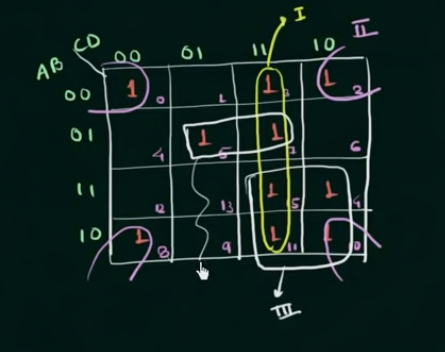
注意四个角, 可圈在一起.
有:
$$
\displaylines
{
F = CD + \overline{BD} + AC + \overline{A}BD
}
$$
注意, 当 K’Map 中所有 cells 都为 1 时, 其结果为 1.
例3
已知: $F(x,y,z,w) = \sum m(1,5,7,9,11,13,15)$
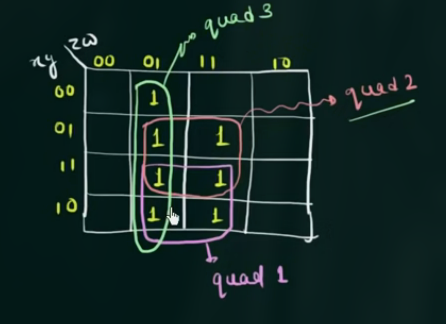
有:
$$
\displaylines
{
F = xw = yw + \overline{z}w
}
$$
48 Don’t Care in K’Map
这里的 Don't Care 表明 K’Map 中不用于构成最简逻辑表达式的部分 (似乎不是这部分的全部)
比如用 4 位输入, 7 位输出, 4 位一共有 15 种组合, 但这里只需要控制 7 个设备, 因此有 8 种组合不需要, 也就是 Don't Care 部分.
例
$$
\displaylines
{
F(A,B,C) = \sum m(2,3,4,5) + \sum d(6,7)
}
$$
(这里的 $\sum d(6,7)$ 就是 Don’t Care 部分)
如果向 K’Map 填入的是 minterm, 则将 d 视为 1.
如果向 K’Map 填入的是 maxterm, 则将 d 视为 0.
一开始的, K’Map 为:
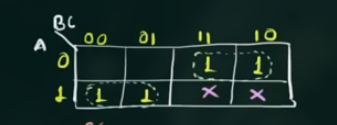
(这里 Don’t Care 画成 X)
将其替换后得:
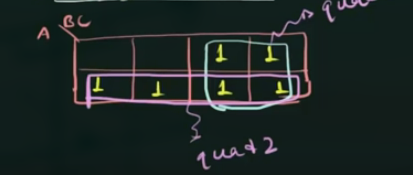
“圈” 变大的好处 , 最简式中每一项中的变量变少.
49 K’Map Using Maxterm
也就是 “圈” 0 为一组.
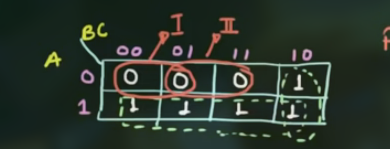
需要注意的是, 此时需要写成 $\overline{F} = …$
因此有:
$$
\displaylines
{
\overline{F} = \overline{AB} + \overline{A} C
}
$$
然后利用 Demorgan’s law 得:
$$
\displaylines
{
F = (A+B)(A+\overline{C})
}
$$
(这看得出是 POS Form)
例2
已知 $F(A,B,C,D) = \sum m (1,3,4,5,9,11,14,15)$
可以将其转化为 Maxterm 形式:
$$
\displaylines
{
F(A,B,C,D) = \prod M (0,2,6,7,8,10,12,13)
}
$$
然后向 K’Map 中填入 0, 并开始 grouping.
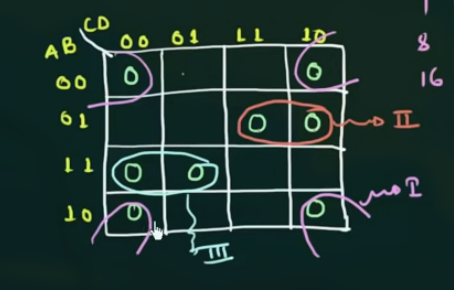
此时以 POS Form 来写表达式, 有:
$$
\displaylines
{
F = (B+D) (A + \overline{B} + \overline{C}) (\overline{A} + \overline{B} + C)
}
$$
50 K’Map with 5 variables
5 个变量的 K’Map 大概长这样:
5 个变量的组合共有: $2^5 = 32$ 种.
51 Quine-McCluskey minimization Technique (Tabular Method)
用例子来解释:
$Y(A,B,C,D) = \sum m (0,1,3,7,8,9,11,15)$ 这里 A 是 MSB, D 是 LSB
minterm 数字的 binary 等价形式.
$$
\displaylines
{
\ \ \ A\ B\ C\ D \newline~ \newline
0-0\ 0\ 0\ 0 \newline~ \newline
1-0\ 0\ 0\ 1 \newline~ \newline
3-0\ 0\ 1\ 1 \newline~ \newline
7-0\ 1\ 1\ 1 \newline~ \newline
8-1\ 0\ 0\ 0 \newline~ \newline
9-1\ 0\ 0\ 1 \newline~ \newline
11-1\ 0\ 1\ 1 \newline~ \newline
15-1\ 1\ 1\ 1 \newline~ \newline
}
$$
Step 1
将这些 minterm 进行分组 (通过 1 的个数) 如:
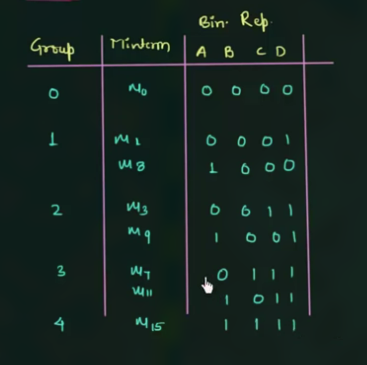
Step 2
将第 n 组和 第 n+1 组进行比较, 将唯一不同的变量消除 (只写有一个变量不同的), 如:

(中间的一列为 matched pair, 只有一个变量不同的就称为 matched pair)
Step 3
根据 step 2 的图继续找 matched pair:

根据最后一列的结果写出 prime implicants (0 为 complement):
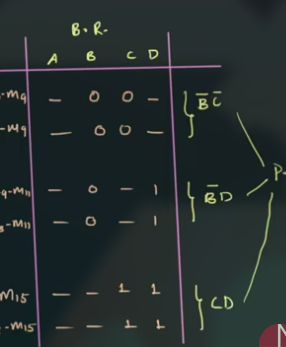
通过最后的 matched pair 画出一个表:
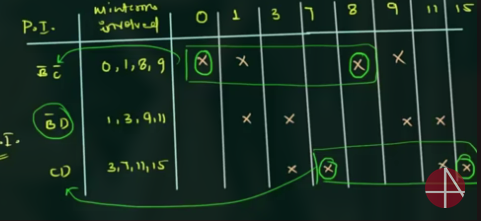
第一排为原式子中的 minterm 下标.
第二排为最后一个 matched pair 表中 group 0 的 minterm 下标.
第三排为最后一个 matched pair 表中 group 1 的 minterm 下标.
第四排为最后一个 matched pair 表中 group 2 的 minterm 下标.
找出只有一个 cross 的列, 写出最简式:
$$
\displaylines
{
Y(A,B,C,D) = \sum m (0,1,3,7,8,9,11,15) \newline~ \newline
= \overline{B} \overline{C} + CD
}
$$
52 一些习题
例 1

最终的式子 $f = A + B’ C$ 只有两项, 可以得到 —- K’Map 有两个 “圈”. $A$ 是第一个 “圈” 的结果, $B’C$ 是第二个 “圈” 的结果.
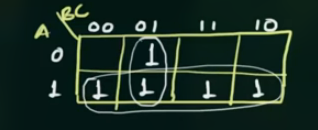
画出 K’Map 后推导出填 1 的位置, 然后可以根据 K’Map 写出 MOP:
$$
\displaylines
{
\sum m(1, 4, 5, 6, 7)
}
$$
例 2

这道题同样需要借助 K’Map, 这里有四个变量, 因此画出的 K’Map 为:
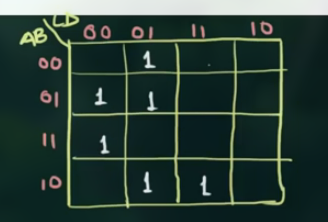
分组并写出表达式:
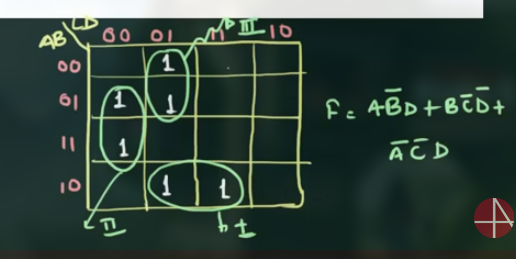
例 3

同样利用 K’Map:
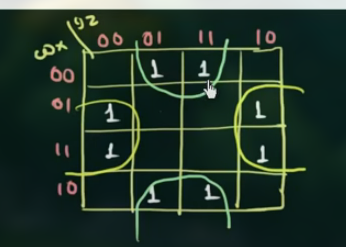
得到:
$$
\displaylines
{
F = z \overline{x} + x \overline{z} \newline~ \newline
= x \oplus z
}
$$
因此可以看出和 $y$ 以及 $w$ 无关
例 4

画出 K’Map 并写出表达式:
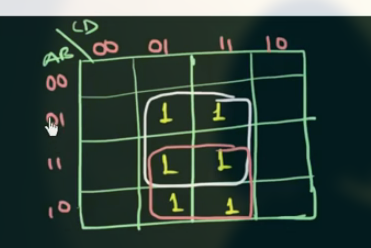
得到:
$$
\displaylines
{
F = BD + AD = (B + A) \cdot D
}
$$
因此和 $C$ 无关.
53 4-bit 偶校验器
当 4-bit 中 1 的个数为奇数时, 输出 1 (这样总的 1 的个数就为偶数), 可以得到真值表为:


填入 K’Map 中得:
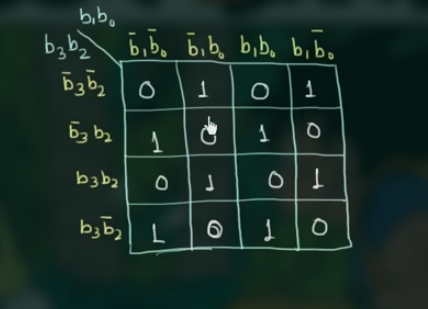
可以发现, 所有的 1 都只能单独组合, 因此:

写出化简的式子:
$$
\displaylines
{
P_o = \overline{b_3} \overline{b_2} \overline{b_1} b_0 + \overline{b_3} \overline{b_2} b_1 \overline{b_0} + \overline{b_3} b_2 \overline{b_1} \overline{b_0} + \overline{b_3} b_2 b_1 b_0 + b_3 b_2 \overline{b_1} \overline{b_0} + b_3 b_2 b_1 \overline{b_0} + b_3 \overline{b_2} \overline{b_1} \overline{b_0} + b_3 \overline{b_2} b_1 \overline{b_0} \newline~ \newline
最终能化简为: \newline~ \newline
P_o = b_0 \oplus b_1 \oplus b_2 \oplus b_3
}
$$
也就是全为 XOR 的电路.
一个结论
当遇到 K’Map 如:

可以直接将所有变量用 XOR 写出, 即:
$$
\displaylines
{
P_o = b_0 \oplus b_1 \oplus b_2 \oplus b_3
}
$$
54 Seven Segment Display Decoder
示意图如:
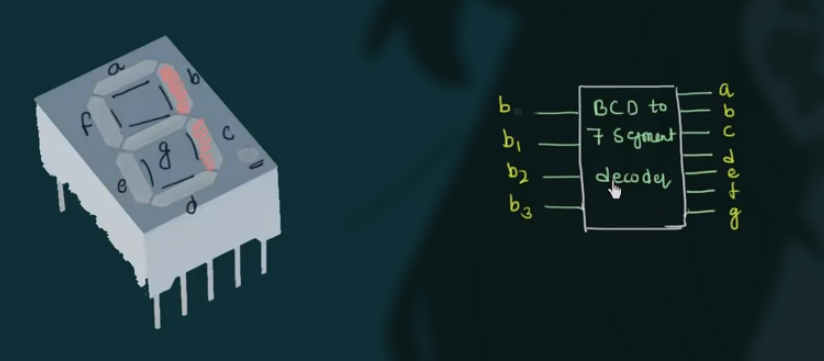
有 8 个 led (有一个小数点) 需要控制, 因此至少需要 4 位的二进制数.
需要关注部分的真值表为:

利用 K’Map 来化简, 每一列都用于创建一个 K’Map ( 即, a 列一个 K’Map, b 列一个 K’Map 等 )
对于 a 列:
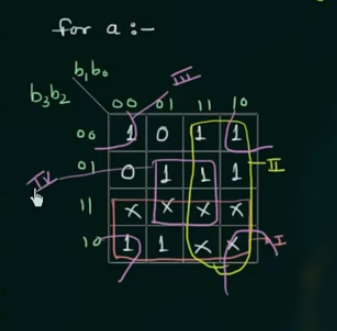
(注意这里的 Don't Care 部分视为 1)
写出化简后的表达式为:
$$
\displaylines
{
a = b_3 + b_1 + \overline{b_2 v_0} + b_2 b_0
}
$$
对于其他列也是这样处理.
最终可以得到 4-bit 对每一个 segment 的表达式.
55 组合和时序电路的比较
组合电路 (Combination Circuit), 输出只和当前输入有关. (如 adder, 加法器)
时序电路 (Sequential Circuit), 输出不仅和当前输入有关, 还和以前的输出有关. (如 counter, 计数器)
存储以前的输出需要用到 flip-flop,
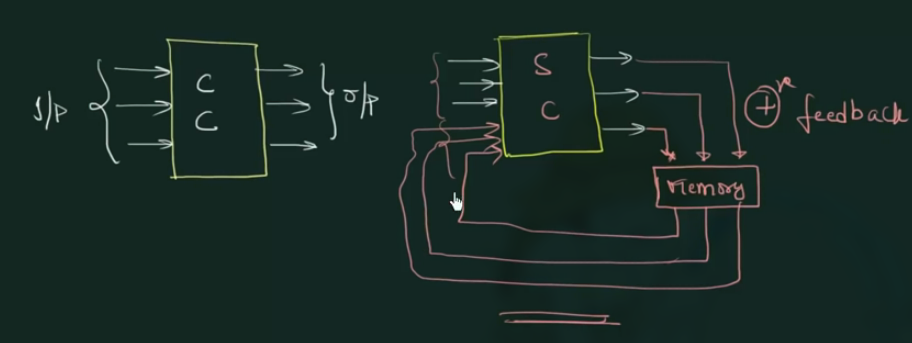
前者为组合电路, 后者为时序电路.
可以看出, 后者先将结果存储在 memory, 然后再输入到原电路, 这被称作 正反馈 (positive feedback)
56 半加器 Half Adder
Half Adder 是一种 combination circuit.
其用于将两个二进制位相加。它有两个输入端,分别是 A 和 B,以及两个输出端,分别是和(Sum)和进位(Carry)。
半加器的特点如下:
只能实现两个一位二进制数的加法。
其不考虑前一位的进位, 当前输出只和本位有关 (如果前一位有进位, 原本应该和现在的两个输入一起相加, 但这里没有考虑)
半加器的输出只有两个,一个是和,一个是进位,不能输出借位。
半加器可以被用作全加器的组成部分,通过级联多个半加器和一个额外的进位输入,实现多位二进制数的加法。
半加器电路简单,通常由一个异或门和一个与门组成,实现简单,成本低廉。
示意图如:
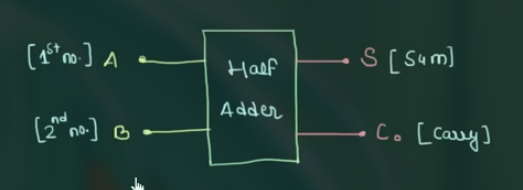
其真值表为:

可直接观察出, 其逻辑表达式为:
$$
\displaylines
{
S = A \oplus B \newline~ \newline
C_o = A \cdot B
}
$$
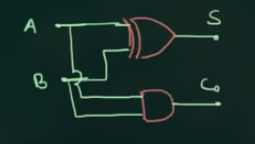
可以借助表达式画出实际电路图:
57 全加器 Full Adder
全加器用于将三个二进制位相加。它有三个输入端,分别是 A、B 和 C_in(前一位的进位),以及两个输出端,分别是和(Sum)和进位(Carry)。
全加器的特点如下:
可以实现三个一位二进制数的加法。
全加器能够考虑到进位问题,将前一位的进位和本位相加,产生本位的进位输出。
全加器能够产生借位,通过将输入的两个二进制位进行异或操作,然后与前一位的进位进行与操作,得到本位的借位输出。
全加器可以被用于级联多个全加器和一个额外的进位输入,实现多位二进制数的加法。
全加器电路相对于半加器要复杂一些,通常由两个异或门、两个与门和一个或门组成,但实现仍然相对简单,成本适中。
其示意图为:
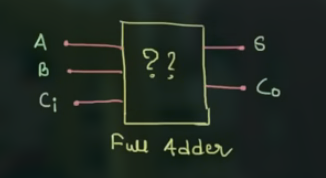
其真值表为:
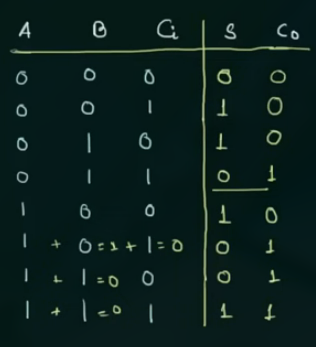
注意 , $C_{in}$ 是前一位的进位, 因此用于得到 Sum (也就是直接和 A, B 相加)
因为有两个输出, 因此需要两个 8 cell 的 K’Map (三个变量因此是 8 cell)
对于 S:
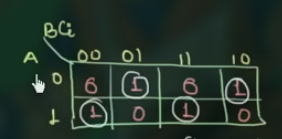
这里的 1 都不能和其他的 1 组合, 这种情况称 check board configuration , 可以直接写出逻辑表达式为:
$$
\displaylines
{
S = A \oplus B \oplus C
}
$$
对于 $C_o$:
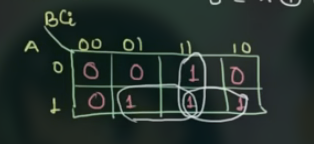
可以写出逻辑表达式为:
$$
\displaylines
{
C_o = BC_i + AB + AC_i
}
$$
但这个逻辑表达式不是我们想要的, 用另一种 K’Map 的组合方法:
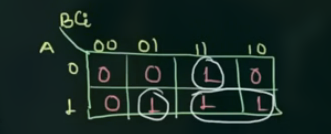
得到的逻辑表达式为:
$$
\displaylines
{
C_o = AB + C_i (A \oplus B)
}
$$
因此可以画出实际电路图为 (这里只有 Sum 的一部分):
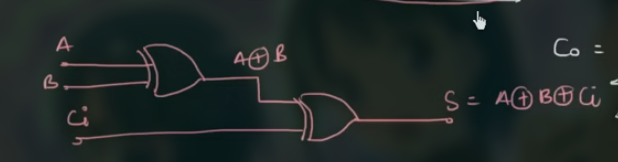
58 用半加器实现全加器
半加器和全加器的区别 在于, 全加器考虑到了进位问题, 半加器只能实现单个二进制位的加法,而全加器可以实现多个二进制位的加法.
两者的示意图为:
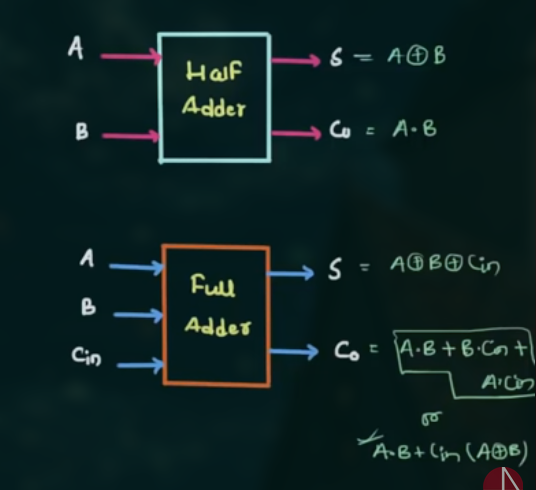
用半加器实现全加器, 实际上就是将一个半加器的 Sum 和 另一个半加器的 $C_o$ 相加.
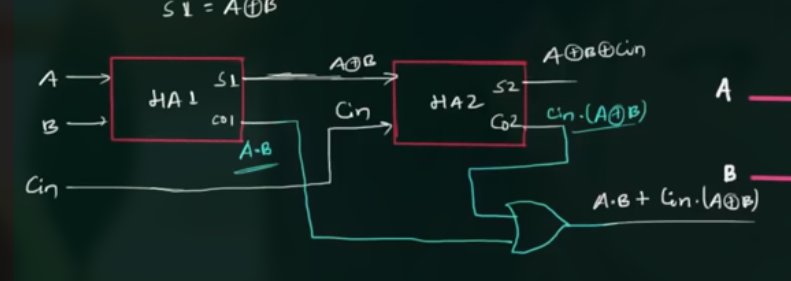
解释
第一个 half adder 的 Sum ( $A \oplus B$ ) 为第二个 half adder 的一个输入, 另一个输入为 $C_{in}$, 就得到了全加器的 Sum $A \oplus B \oplus C_{in}$
第一个 half adder 的 $C_{o}$ ($A \cdot B$) 和第二个 half adder 的 $C_{o}$ ($C_{in} \cdot (A \oplus B)$) 相或, 就得到了全加器的 $C_{o}$, 即 $A \cdot B + C_{in} \cdot ( A \oplus B )$.
主要就是将两个逻辑表达式表示出;
$$
\displaylines
{
S = A \oplus B \oplus C \newline~ \newline
C_o = AB + C_i (A \oplus B)
}
$$
59 用全加器实现 Four Bit Parallel Adder
Four bit parallel adder 就是指:

两个二进制数相加, 每个为 4 bits.
其工作流程为:
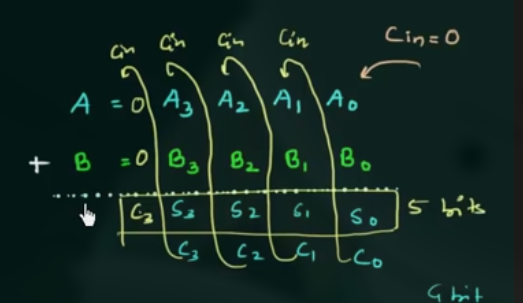
解释
传入第一个 full adder 的 $C_{in} = 0$, 对于第一个 full adder 而言, $S_0 = C_{in} + A_0 + B_0$, 根据进位得到 $C_0$.
$C_0$ 作为第二个 full adder 的 $C_{in}$ 输入, 有, $S_1 = A_1 + B_1 + C_{0}$, 根据进位得到 $C_{1}$
…
以此类推.
- 如果 $C_3$ 是 1, 则结果为 5 bits.
- 如果 $C_3$ 是 0, 则结果为 4 bits.
反应到图中为:
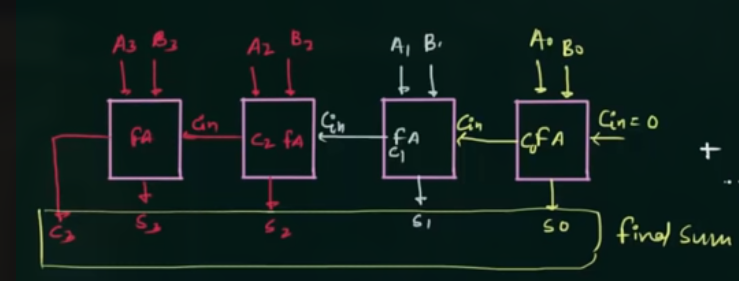
简化为一个器件的图为:
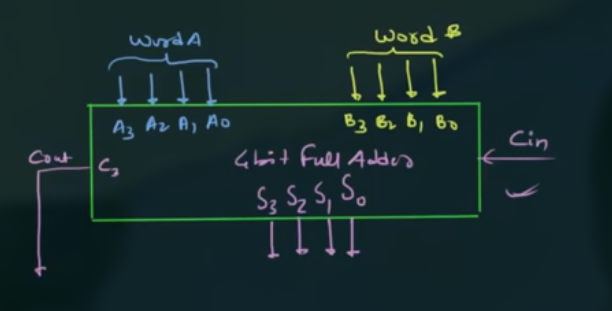
可以用两个 four bit parallel adder 得到一个 eight bit parallel adder:
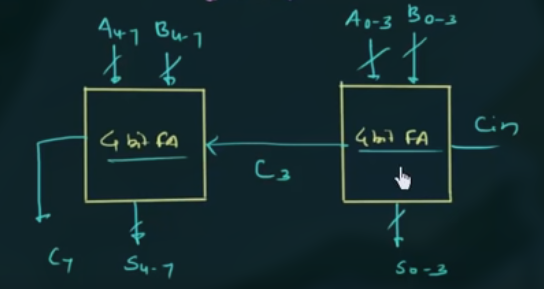
60 半减器 Half Subtractor
其用于将两个一位二进制数进行减法运算,并产生差(Difference)和借位(Borrow)输出. (同样无法实现多位减法)
示意图如:
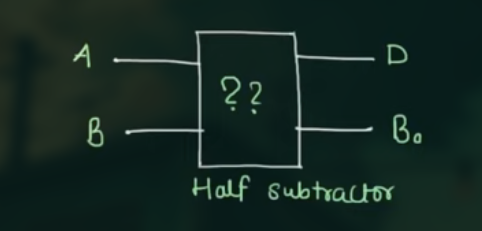
真值表为:
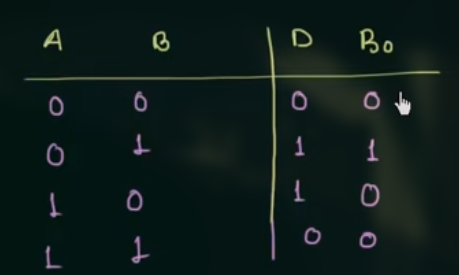
根据真值表可以得到逻辑表达式为:
$$
\displaylines
{
D = A \oplus B \newline~ \newline
B_o = \overline{A} B
}
$$
(其实就是直接写 SOP Form 表达式)
其逻辑图为:
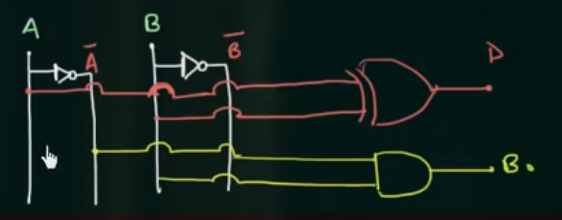
61 全减器 Full Subtractor
其用于将三个一位二进制数相减 (分别为被减数、减数和来自低位的借位),并产生其差(Difference)和借位(Borrow)输出.
示意图为:
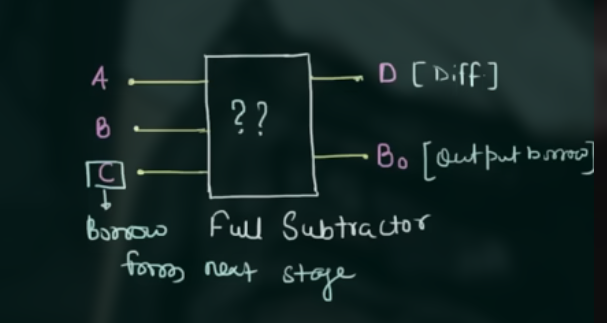
其真值表为:

这里有两个输出, 因此借助两个 K’Map 来得到最简的逻辑表达式.
对于 $D$:
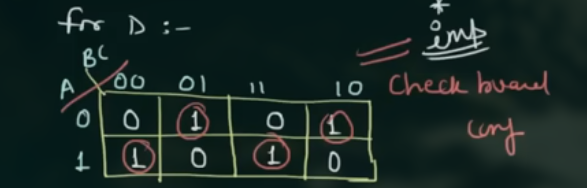
这里同样是 check board configuration, 因此可以直接得到表达式为:
$$
\displaylines
{
D = A \oplus B \oplus C
}
$$
对于 $B_o$:
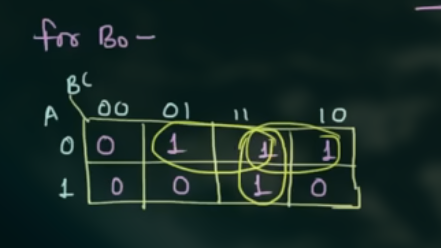
可以得到表达式为:
$$
\displaylines
{
B_o = BC + \overline{A} C + \overline{A}
}
$$
62 只用 NAND Gate 实现 Half Adder
已知 Half Adder 的 sum 和 carry 的计算为:
$$
\displaylines
{
\begin{aligned}
S = A \oplus B \newline~ \newline
C_O = A \cdot B
\end{aligned}
}
$$
实现 $S = A \oplus B$ 的电路为:
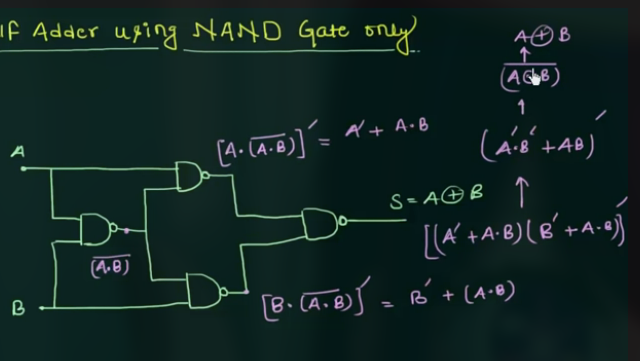
实现 $C_O = A \cdot B$ 只需要:
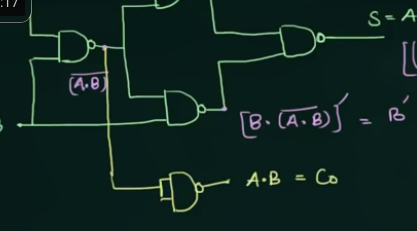
63 只用 NOR Gate 实现 Half Adder
同样已知 Half Adder 的 sum 和 carry 的计算为:
$$
\displaylines
{
\begin{aligned}
S = A \oplus B \newline~ \newline
C_O = A \cdot B
\end{aligned}
}
$$
分析
在 NOR Gate 中, 想要得到 $A \cdot B$, 需要输入为 $A’$ 和 $B’$, 此时就有:
$$
\displaylines
{
\begin{aligned}
(A’ + B’)’ = A \cdot B
\end{aligned}
}
$$
因此可以用三个 NOR Gate 来形成这个 AND Gate:
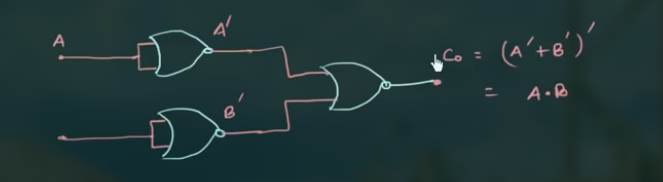
而:
$$
\displaylines
{
\begin{aligned}
S = A \oplus B = A’B + B’A \newline~ \newline
= \overline{A’B’ + AB}
\end{aligned}
}
$$
此时已有 $AB$, 因此只需要得到 $A’B’$, 即:
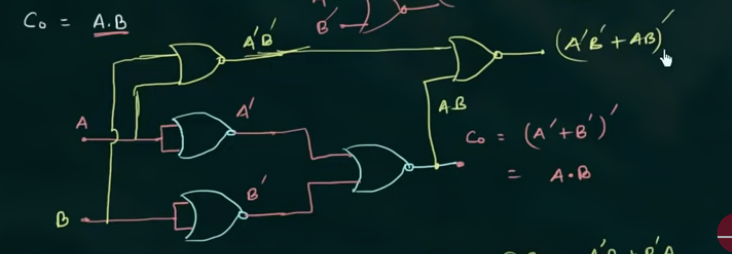
64 只用 NAND Gate 实现 Full Adder
已知 Full Adder 的 Sum 和 Carry 的计算为:
$$
\displaylines
{
\begin{aligned}
S = A \oplus B \oplus C_i \newline~ \newline
C_o = A \cdot B + C_i (A \oplus B)
\end{aligned}
}
$$
分析
得到 Sum 需要两个 XOR Gate 如:
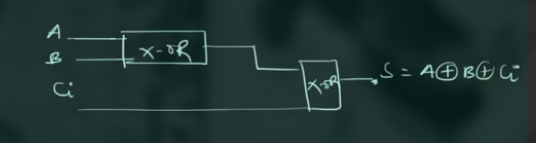
其具体电路实现为:
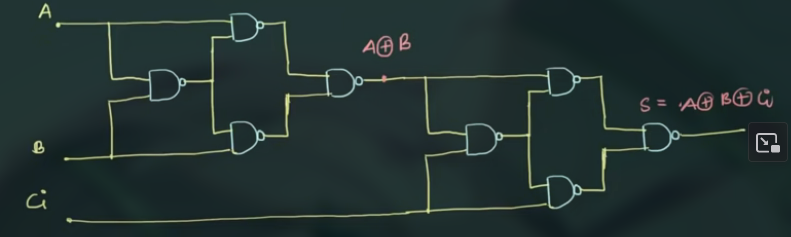
得到 Carry 如:
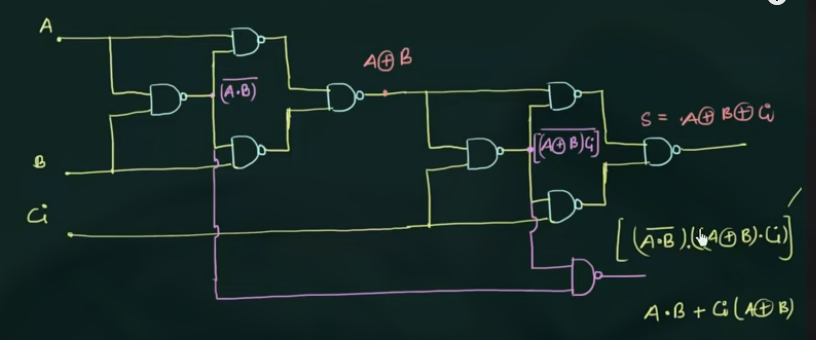
65 只用 NAND Gate 实现 Half Subtractor
已知 Half Subtractor 的 Difference 和 Borrow 的计算为:
$$
\displaylines
{
\begin{aligned}
D = A \oplus B \newline~ \newline
B_0 = A’ B
\end{aligned}
}
$$
66 SR Latch|NOR and NAND SR Latch
SR 中的 “S” 为 “Set”, “R” 为 “Reset”
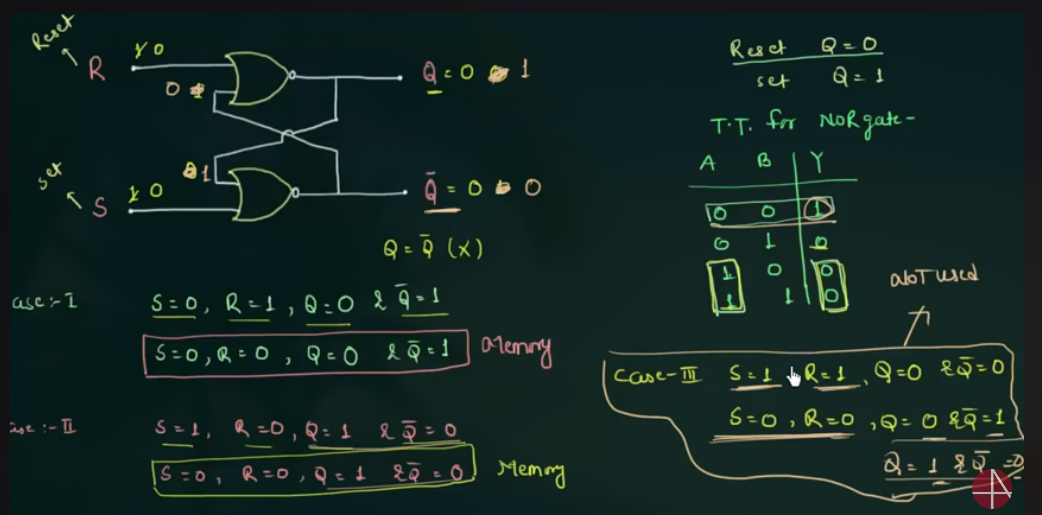
SR Latch 的 truth table:
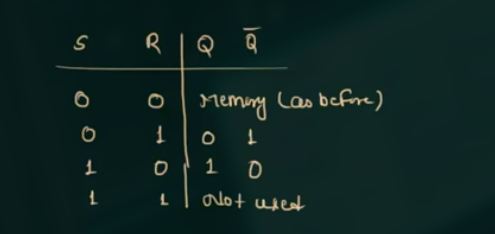
NAND 组成的 SR Latch:
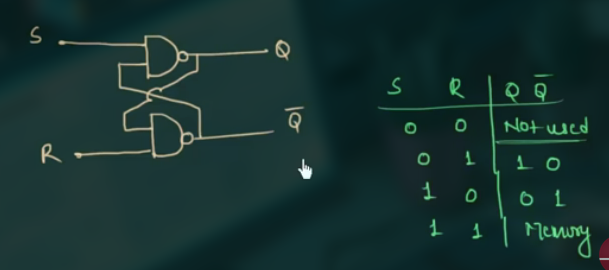
67 What is Clock
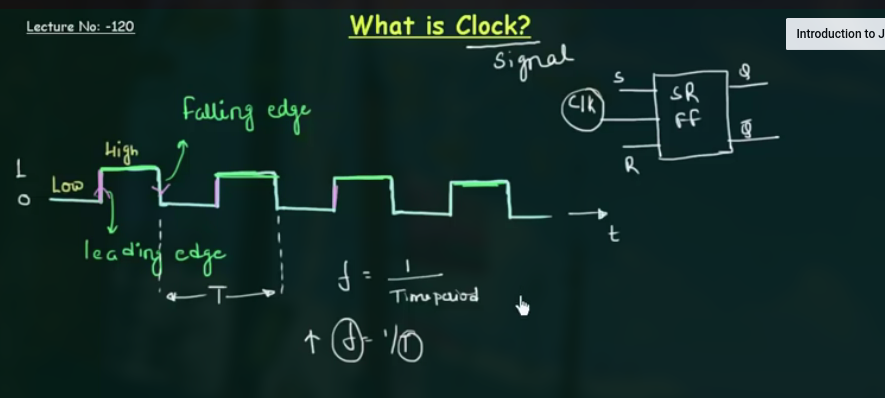
注意一个概念 duty cycle , $\frac{signal function}{total time}$
68 Triggering Methods
两种 trigger 的方法:
- level
- edge
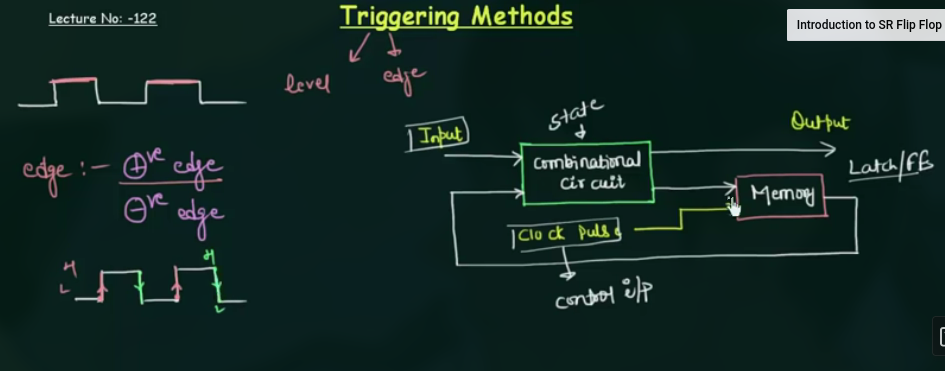
69 Differce between Latch and Flip Flop
Latch 的 control signal 是 En, 其为 level sensitive:
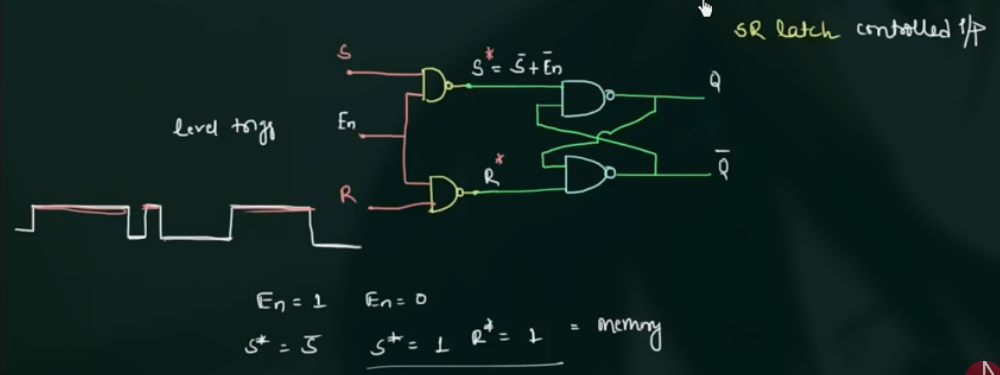
flip-flop 的 control signal 是 clock, 且为 edge triggering:
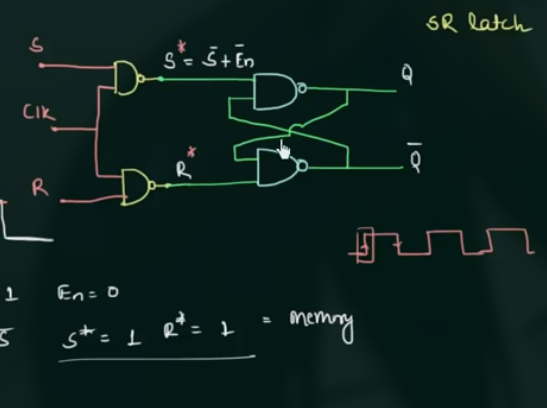
70 Introduction to SR Flip Flop
其电路图, 表示符号, 逻辑表达式为:
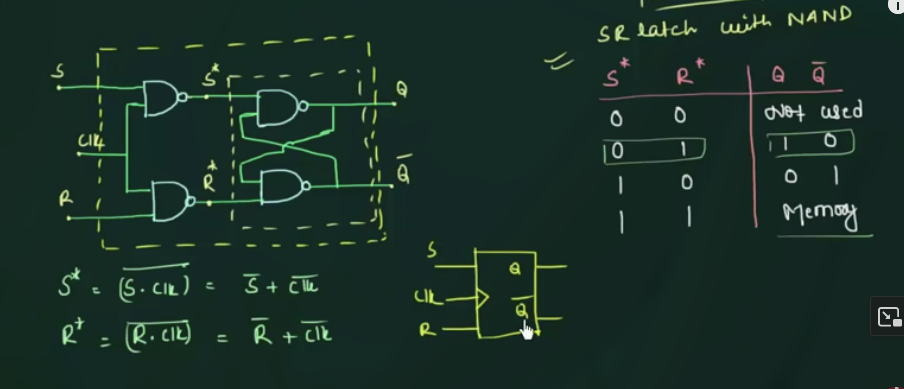
真值表为:
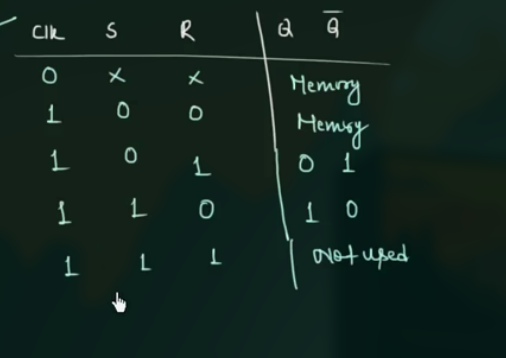
71 Characteristic table & excitation table for SR flip flop
SR flip-flop 的 truth table 和 characteristic table:
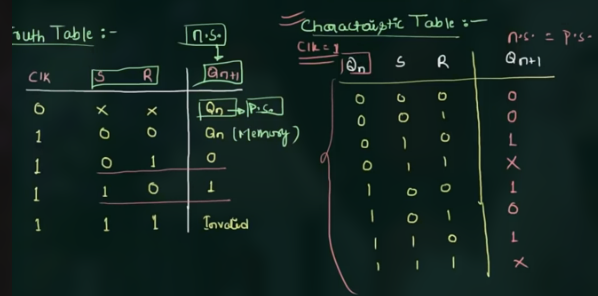
SR flip-flop 的 exitation table:
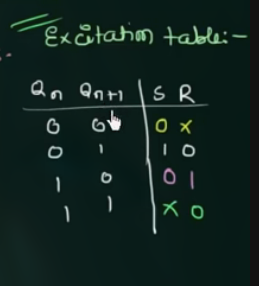
72 Introduction to D flip flop
已知 SR flip-flop 的信息为:
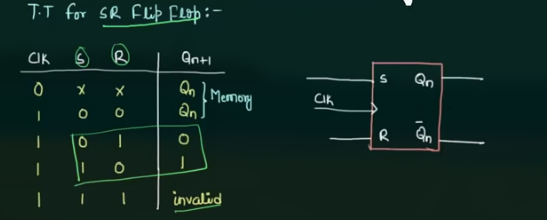
可以看出, 进行数据存储变化的情况下, S 和 R 都是 implement 的, 因此, 通过用一个反相器, 就得到了 D flip-flop (“D” 是 Data 的意思):
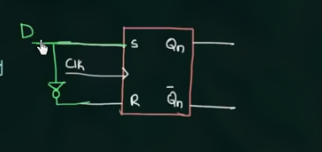
简化为:
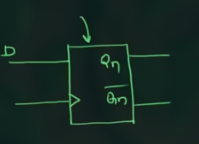
得到 truth table 为:
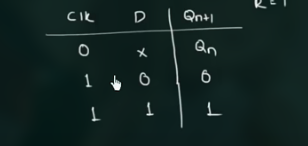
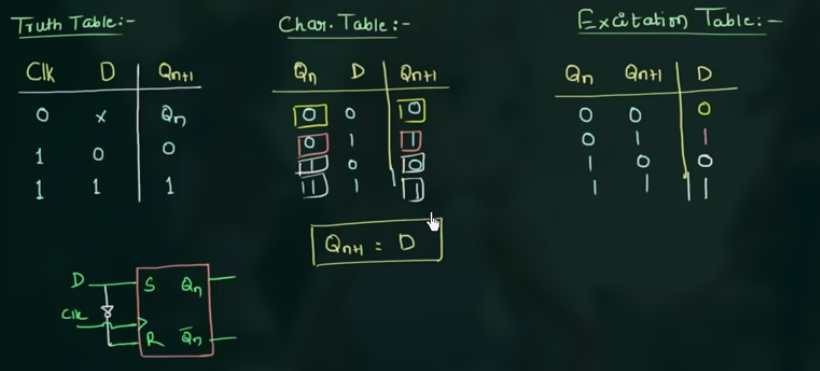
73 Characteristic table & excitation table for D ff
3 个重要的 tables:
74 Introduction to JK flip flop
JK flip flop 的作用是, 将下面 $S=1$ 和 $R=1$ 的情况利用起来:
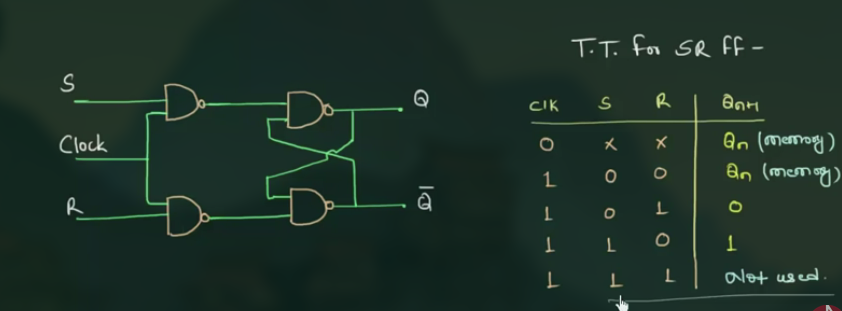
将输出反馈到输入中, 就从 SR flip-flop 转变为 JK flip-flop:
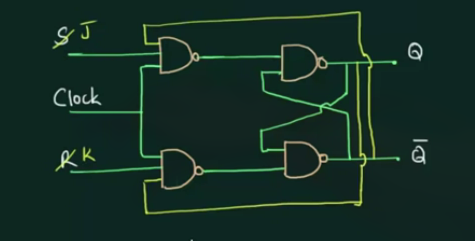
其特点为: 当J和K输入都为1时,JK触发器会将输出取反.
75 Characteristic and Excitation table for JK ff
JK ff 的 truth table 和 Characteristic table 为:
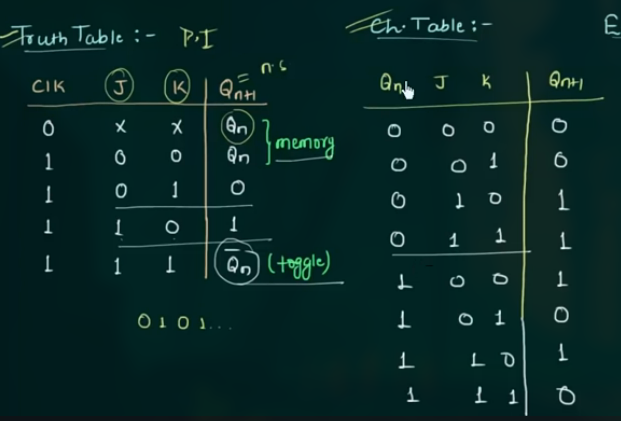
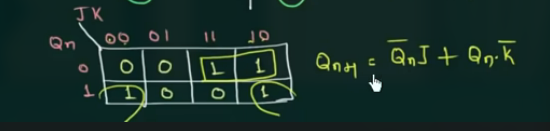
$Q_{n+1}$ 的 logic expression 为:
注意什么时候用 don’t care.
其 excitation table 为:
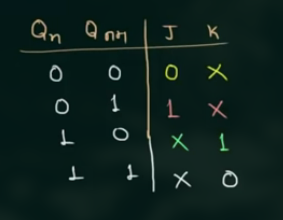
根据这个 table 得到的 J 和 K 的逻辑表达式为:
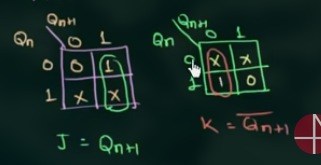
76 Race Around Condition
JK flip-flop是一种基本的数字电路元件,它可以存储一个比特(0或1)的状态,并且可以根据时钟信号进行状态的更新。当时钟信号的边沿(上升沿或下降沿)到来时,JK flip-flop会根据输入J和K的状态来决定更新后的输出状态。
Race Around Condition是一种可能会发生在JK flip-flop中的故障状态。当J和K同时为1时,JK flip-flop会处于不稳定的状态,此时输出会来回切换,这种状态称为Race Around Condition。
当J和K都为1时,JK flip-flop会将输出反转,从1变成0或从0变成1。如果此时时钟信号还没有结束,那么JK flip-flop会再次根据J和K的状态更新输出状态,这样就会出现来回切换的状态,直到其中一个输入信号变成0为止。
为了避免Race Around Condition的发生,通常会在JK flip-flop的输入端加上一个使J和K不能同时为1的逻辑电路,例如将J和K连接到一个AND门,这样只有当J和K都为1时才会输出1,否则输出0。这样可以保证JK flip-flop不会进入不稳定的状态。
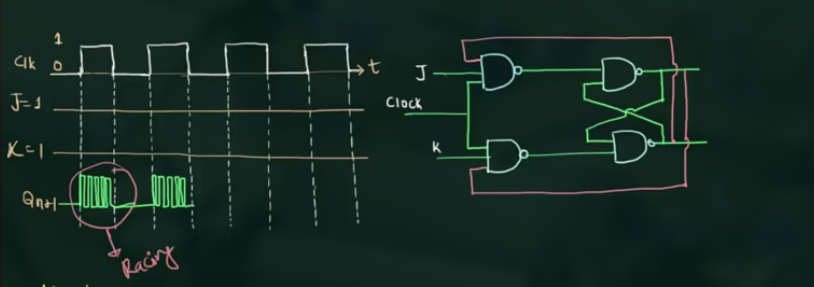
用:
- Edge clock
- master slave
可以避免这个问题.
77 Master-Slave Operation of JK flip flop
电路图为:
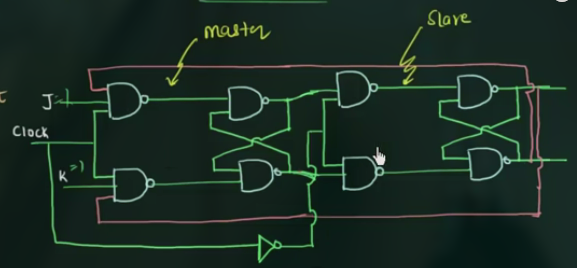
当 clock 为 high 时, master 会 function, 而 slave 不会.
此时, 一个周期 output 只会改变一次. 在 clock 为 low 时, feedback 不会起作用.
其时序图为:

78 Behaviour of Master Slave D Flip Flop
这里, $Q_m$ 是 clock 为 high 时的输出, $Q_P$ 是 clock 变化为上升沿时改变输出, $Q_N$ 是 clock 变化为下降沿是改变输出:
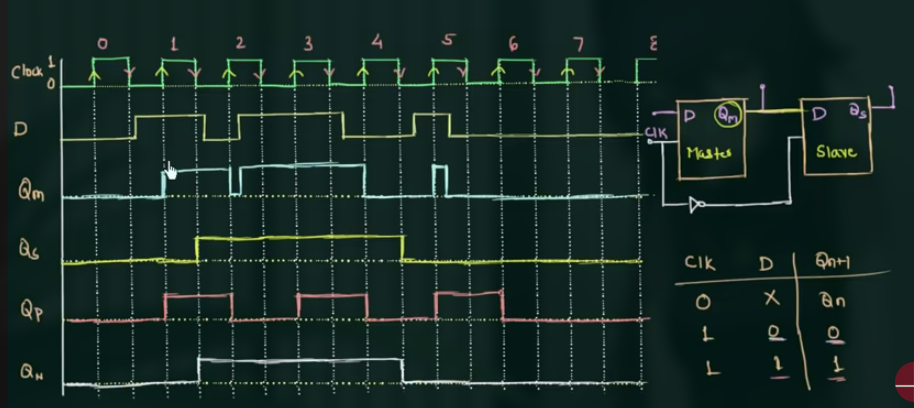
79 Introduction to T flip flop
由 JK flip flop 得到 T flip flop:
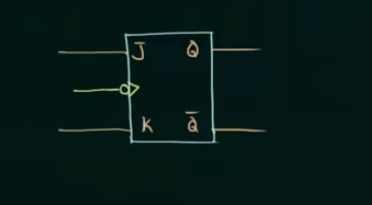
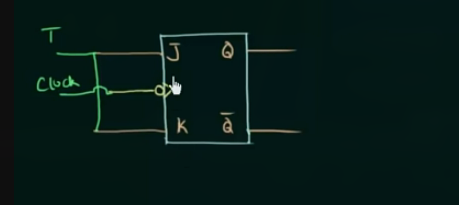
这里利用了 JK flip-flop 的特性, 当 JK 两端同时输入 1 时, 输出会取反.
其 truth table 为:
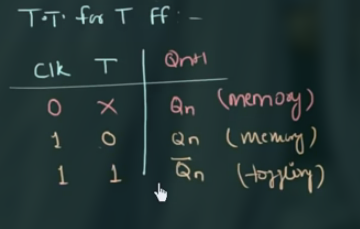
80 Characteristic and Excitation Table for T FF
注意 3 个 tables 之间的关系:
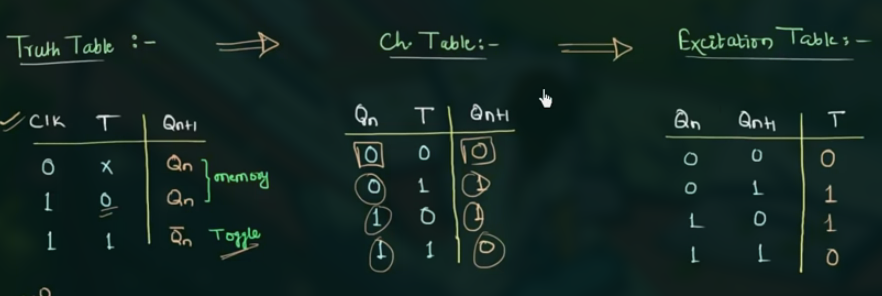
同时可以得到逻辑表达式为:
$$
\displaylines
{
\begin{aligned}
Q_{n+1} = Q_n \oplus T
\end{aligned}
}
$$
81 steps for Flip Flop Conversions | JK to D Flip Flop Conversion
步骤为:
- 找到已知的 flip flop 以及需要转换成的 flip flop
如:
- 已知 JK flip flop
- 求 D flip flop
- 画出要转换成的 flip flop 的 characteristic table
这里为 D flip flop:
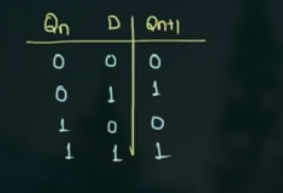
- 画出已知 flip flop 的 excitation table, 和上图画在一起, 先单独画, 再合在一起
这里为 JK flip flop:
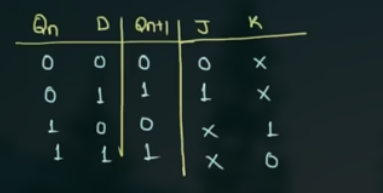
- 写出已知 flip flop 的 input 的 logic expression, 注意用哪些变量来写
这里为 J 和 K:
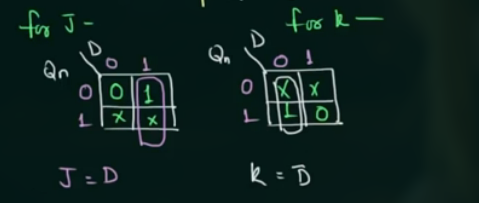
- 根据 logic expression 画出电路图
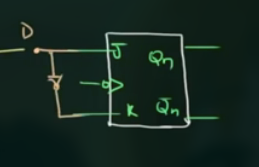
82 T Flip Flop to Flip Flop Conversion
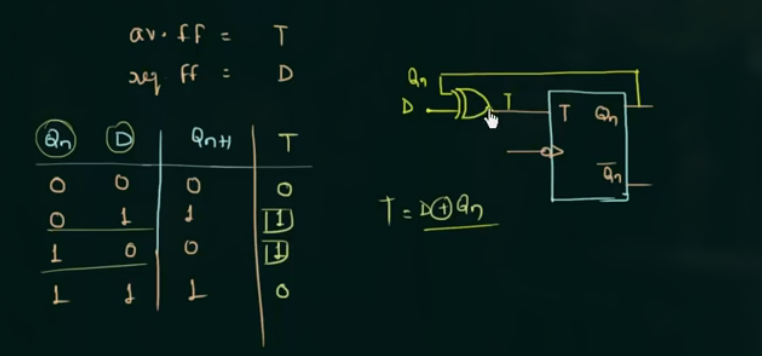
83 SR Flip Flop to JK Flip Flop Conversion
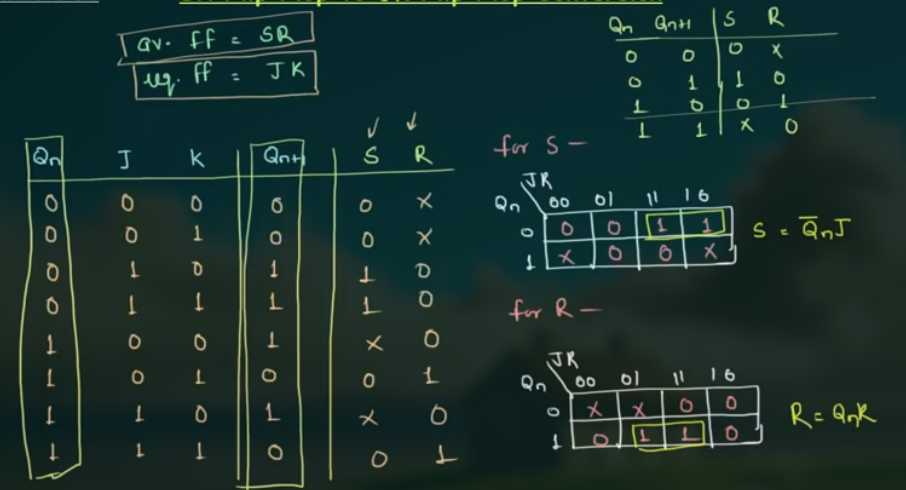
可以画出电路为:
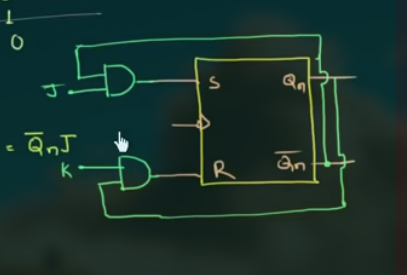
84 SR Flip Flop to T Flip Flop Convertion
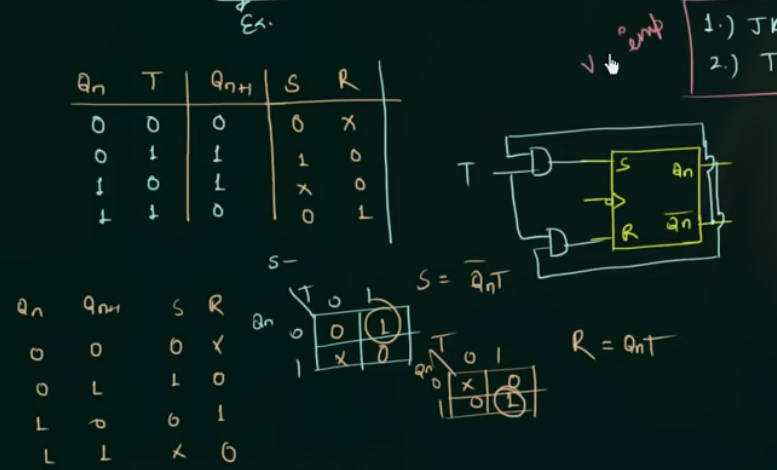
85 Preset and Clear Inputs
将 Preset 信号和 Clear 信号加入到 SR flip flop 中:
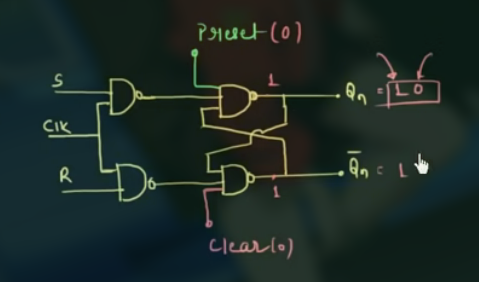
有:
$$
\displaylines
{
\begin{aligned}
preset = 0 \rightarrow Q_n = 1 \newline~ \newline
clear = 0 \rightarrow Q_n = 0
\end{aligned}
}
$$
简化图为:
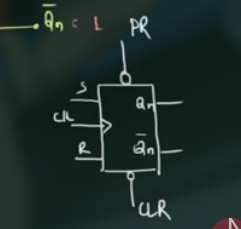
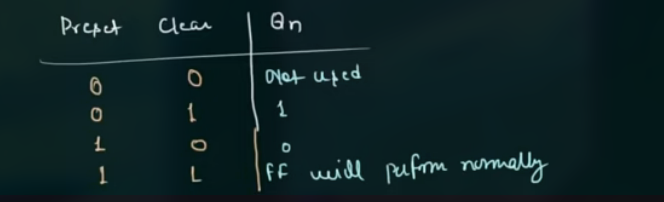
其真值表为:
86 Introduction to State Diagram
State table 是用来表示 present state, next state 和 output 之间的关系
如 $Q_n$ 是 present state, $Q_{n+1}$ 是 next state, JK 是 input, 则通过 JK flip-flop 的真值表画出 State Diagram:
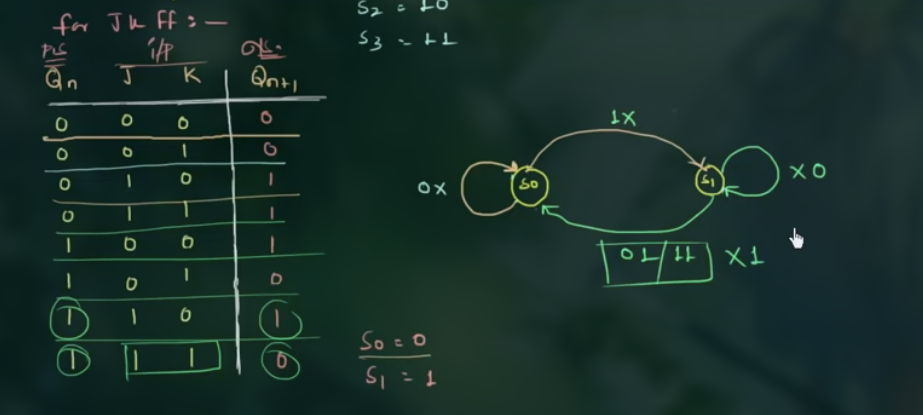
State equation 的 left hand statement 是 $Q_{n + 1}$, right hand statement 是 present state 以及 input signal
如这里为:
$$
\displaylines
{
\begin{aligned}
Q_{n+1} = \overline{Q_{n}} J + Q_n \overline{K}
\end{aligned}
}
$$
87 Design Procedure for Clocked Sequential Circuits
- 画出 State diagram 或者 timing diagram
如:
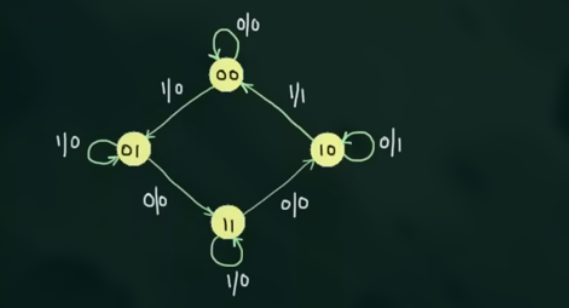
- 根据 State diagram 得到 state table
这里的 $P \cdot S \cdot$ 和 $N \cdot S \cdot$ 分别指代 Present state 和 Next state, 注意 state table 的画法, 包含 3 列:
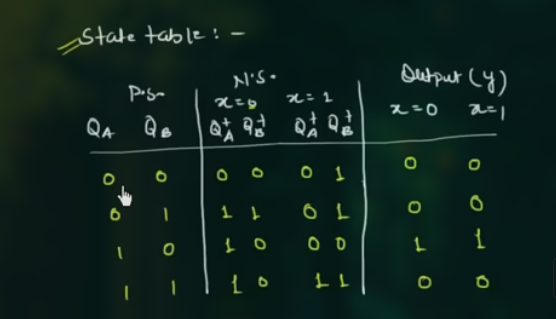
用 state reduction method 来消除一些 states
Do state assignment
有时, 每一个状态只被命名为如 a, b, c, d. 这里则需要将其分配为二进制,
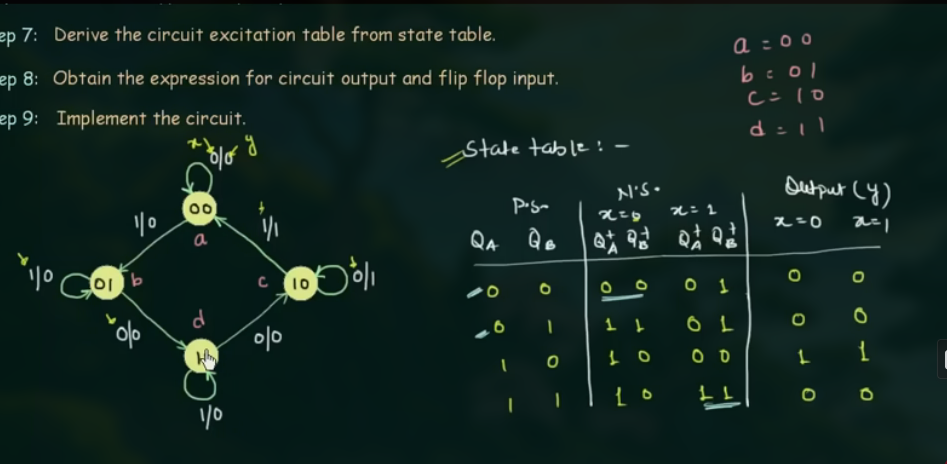
(这道题不需要)
- 决定需要的 flip-flops 的数量以及为它们分配字母
有几位就分配几个 flip-flops, 如这里只有 $Q_A Q_B$ 两位, 则只需要 2 个 flip-flops 可以编号为 A, B:
- 决定 flip-flops 的类型
这里用 T flip flop.
- 利用 state table 得到 excitation table
有 4 列:
- present state 和 x
- next state
- flip flop input
- output

- 获取 circuit output 和 flip flop input 的 logic expression
一般情况需要用 K’Map, 但如果 1 很少, 可以直接写.
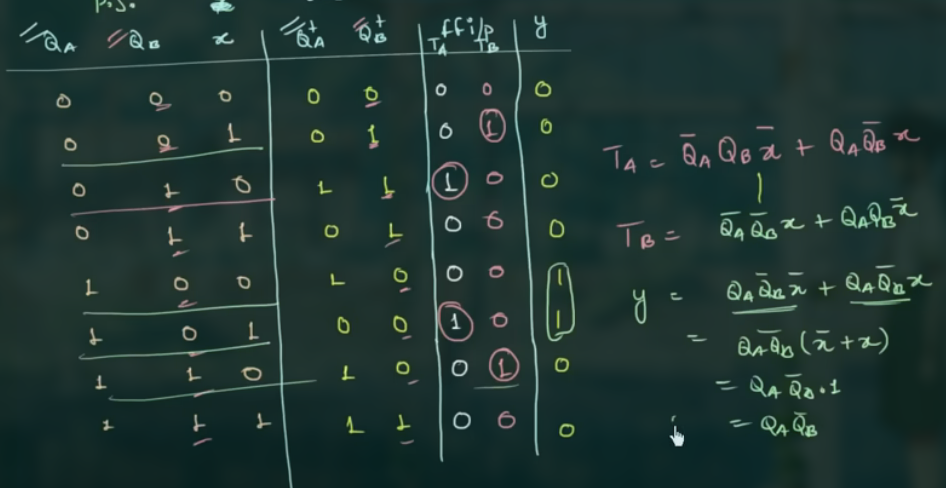
- 根据逻辑表达式作图
88 Mealy and Moore State Machines
- Moore state machine, 其 output 只和 present state 有关
- Mealy state machine, 其 output 和 present state 以及 input 有关
Moore state machine 的流程图:
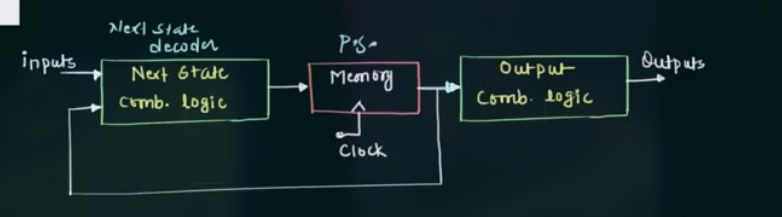
电路图示例:
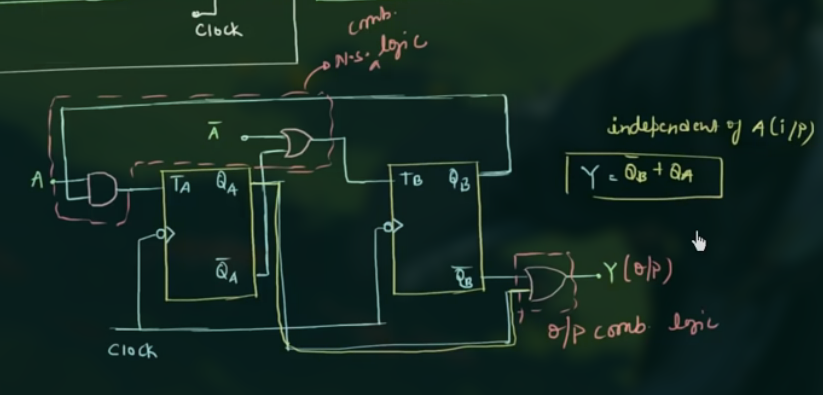
State diagram 示例:
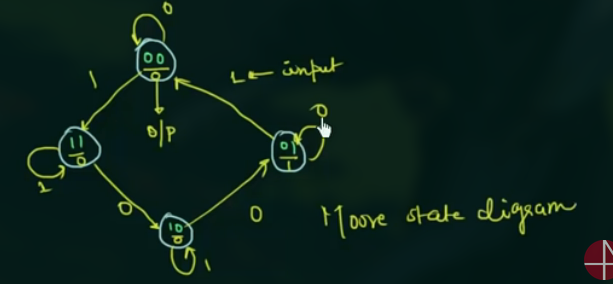
注意将 output 写在圈中.
Mealy state machine 的流程图:
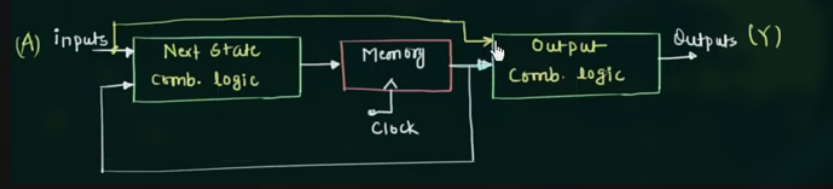
电路图示例:
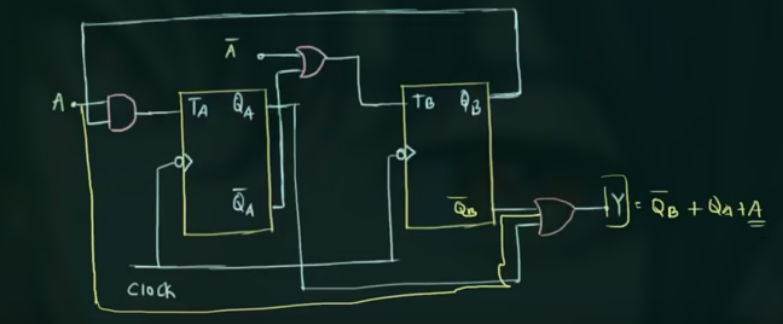
一般情况下, Mealy state machine 所用的 state 数要少于 Moore state machine.
89 Analysis of Clocked Sequential Circuits (with D Flip Flop)
示例电路图:
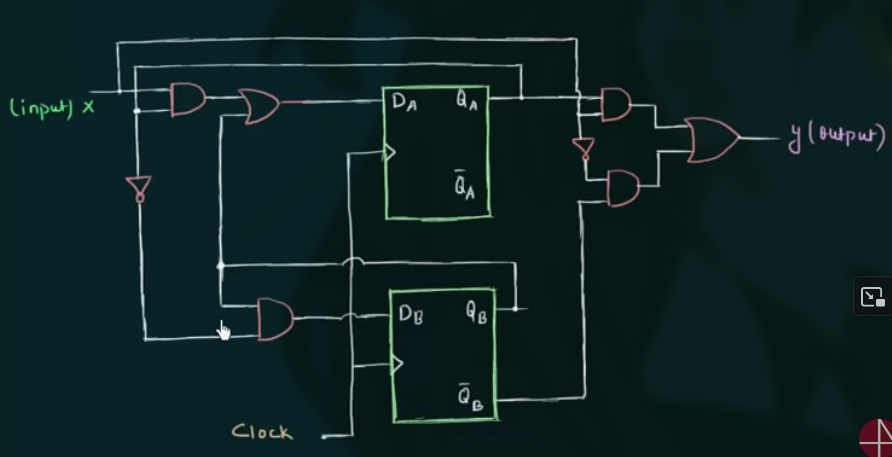
有几个步骤.
- 找出 input 和 output equations
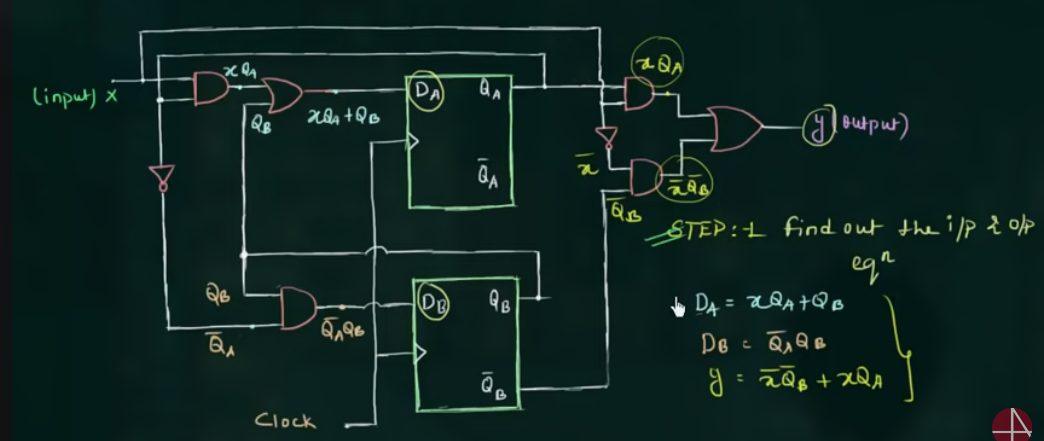
- 画出 state table
先写出 $Q_A^+$ 和 $Q_B^+$ 的表达式.

- 找出 state diagram
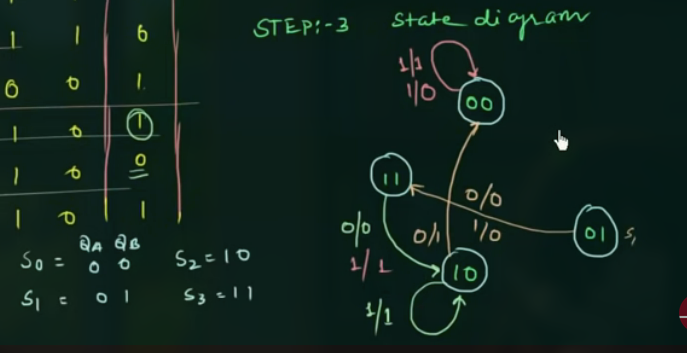
90 Analysis of Clocked Sequential Circuits (with JK Flip Flop)
- 找出 input 和 output equations
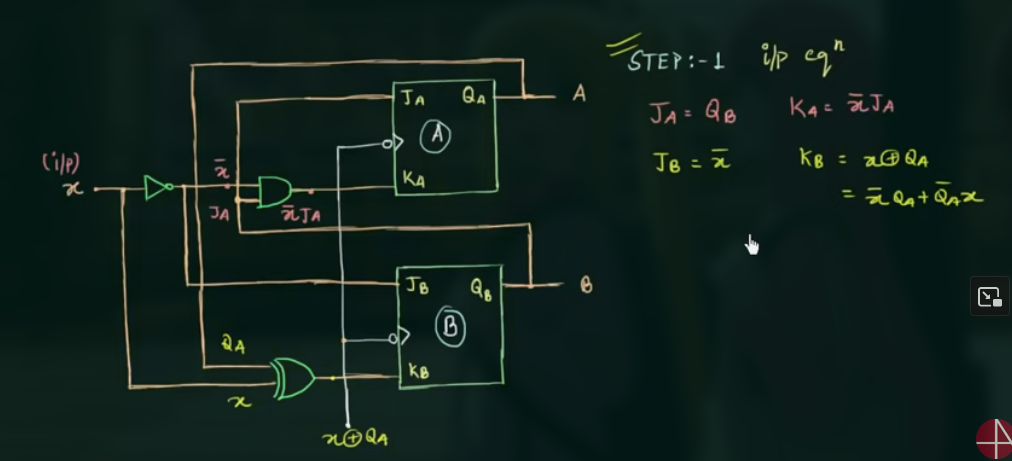
- 画出 state table
注意 output 不只是写成一列, 可以是多列.
一开始可以写出:
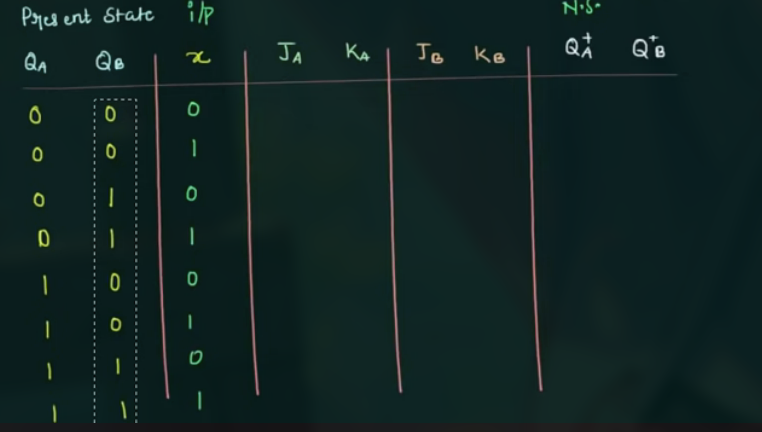
注意 $Q_A$, $Q_B$, $Q_A^+$ 和 $Q_B^+$ 的分开计算.
需要对 flip-flop 的真值表很熟悉.
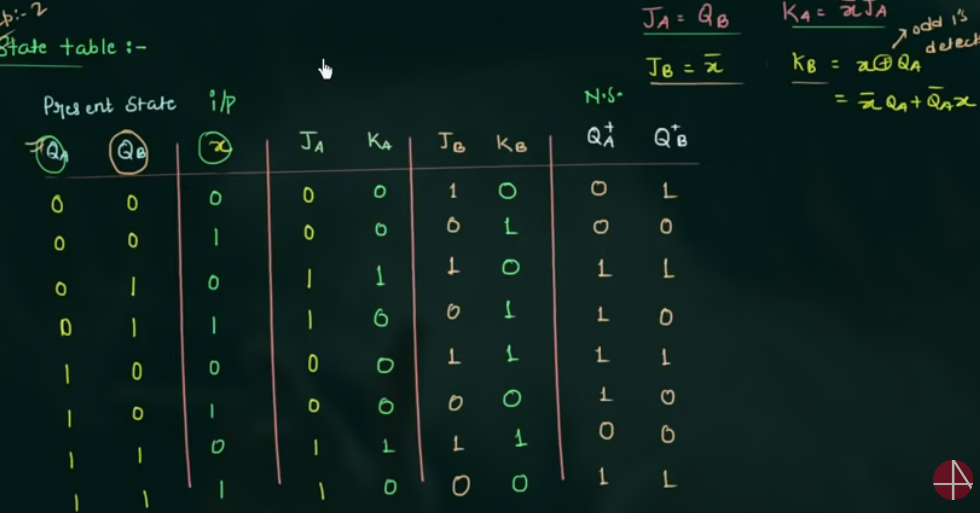
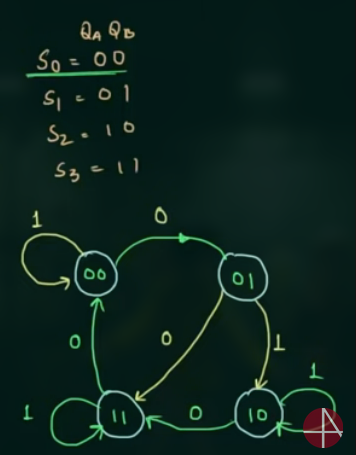
- 画出 state diagram
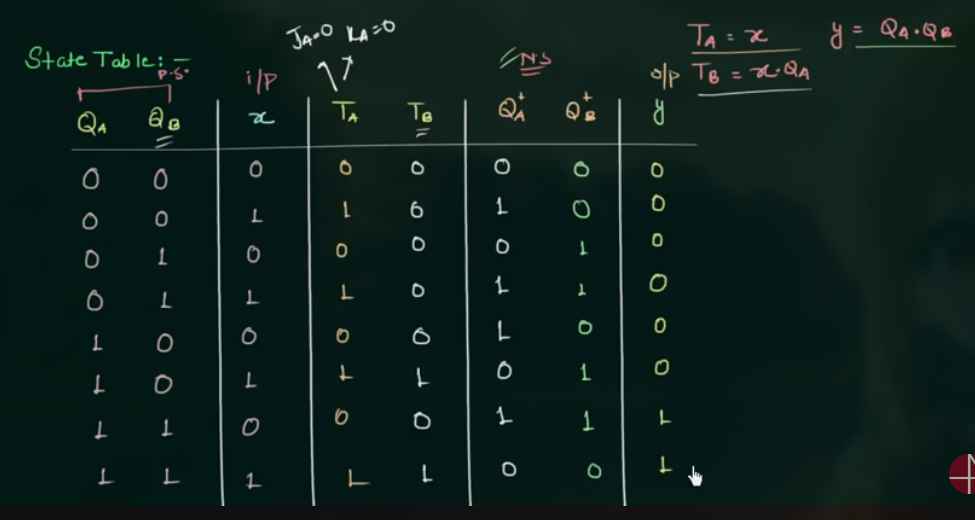
90 Analysis of Clocked Sequential Circuits (with T Flip Flop)
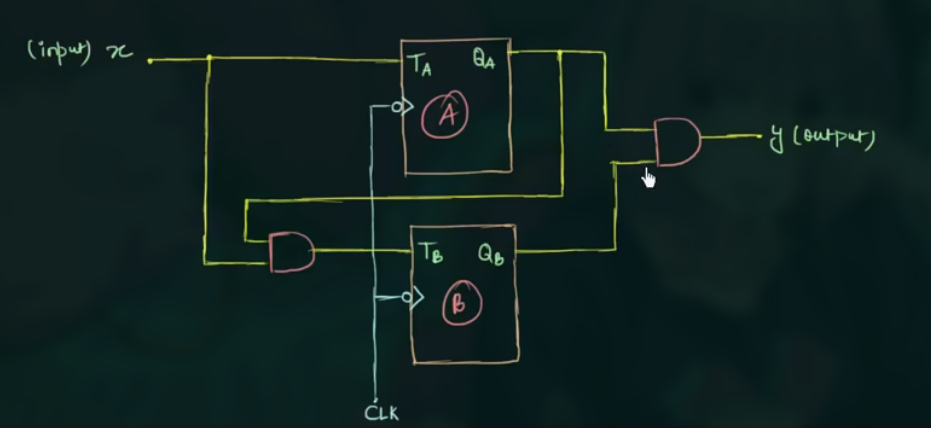
- 找出 input 和 output equations
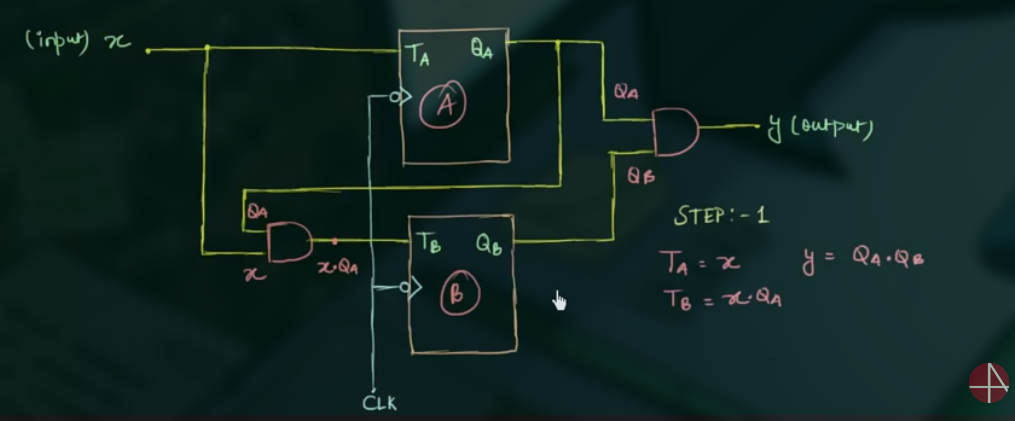
- 画出 state table
注意画 input 时不只是 x, 同时有 $T_A$ 和 $T_B$, 因为这两个才是 flip flops 的 input
- 画出 state diagram
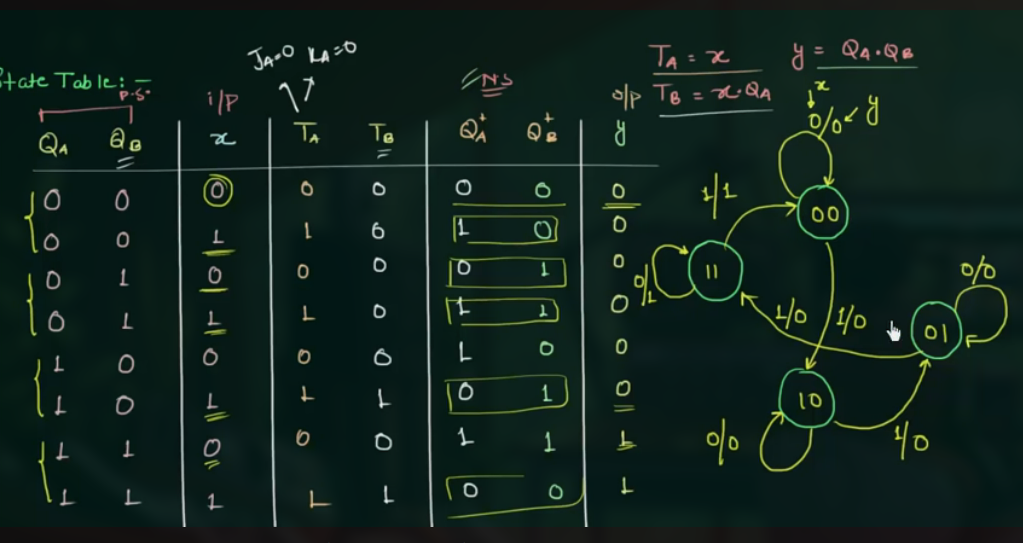
91 Pattern or Sequence Detector
即序列检测器.
输入一个序列, 在 clock 为 high 时开始检测, 而当序列检测出时, output 为 high.

示例 input 和 output:

设计 Sequence Detector 的步骤:
- 画出 state diagram (mealy machine)

- state assignment
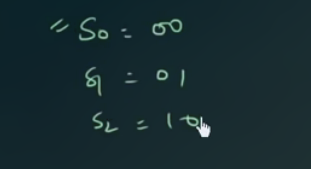
92 Pattern or Sequence Detector (Example)
注意 overlamping 和 non-overlamping 的区别:
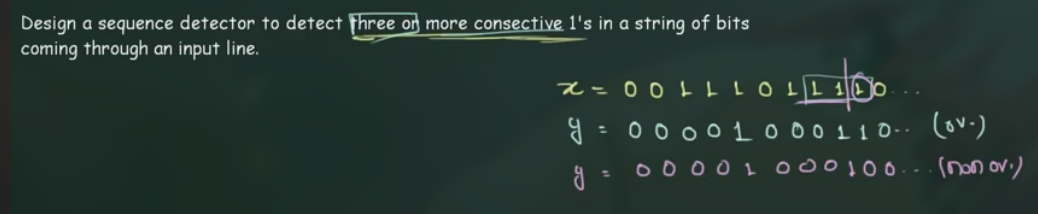
- 写出 states:

- 可以得出 states diagram:
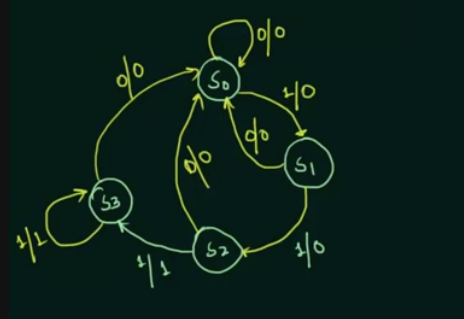
State assignment:
$$
\displaylines
{
\begin{aligned}
s_0 = 00 \newline~ \newline
s_1 = 01 \newline~ \newline
s_2 = 10 \newline~ \newline
s_3 = 11
\end{aligned}
}
$$得出 State table:

- 得出 output 的 logic expression:
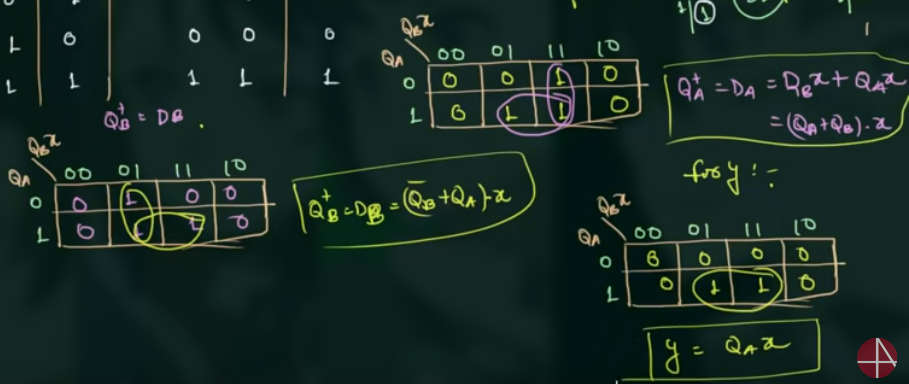
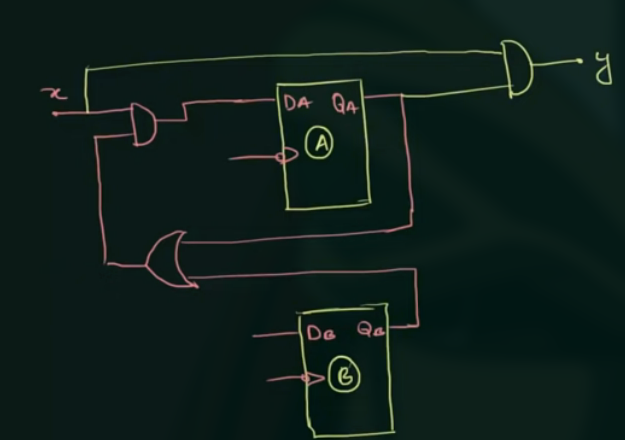
- 画出电路图
这里没画完.
93 State Reduction and Assignment
State Assignment 就是为每一个状态分配一个二进制数.
State Reduction 的原则: 两个状态的 Next state 列和 output 列都相同, 则可以消除.
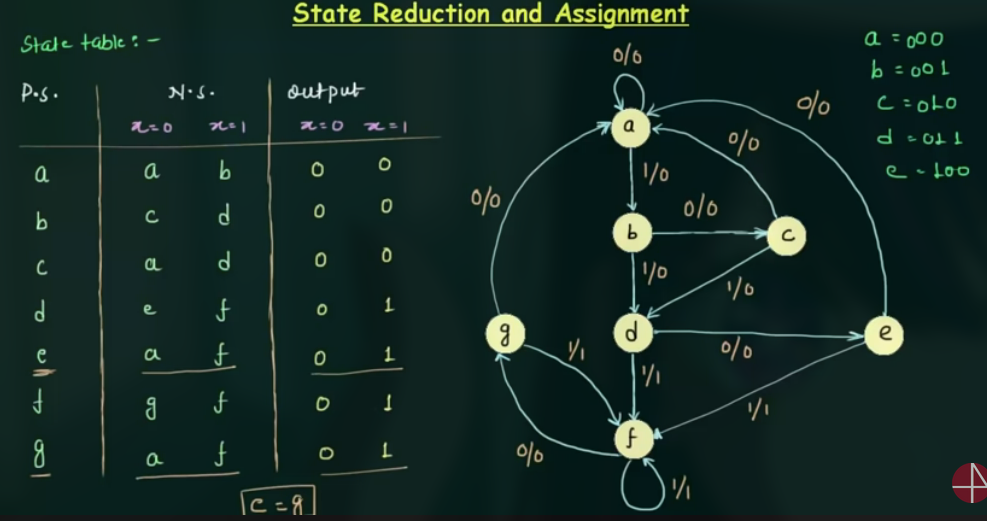
(这里还有需要消除的)
消除之后重新绘制 state diagram.
94 Difference between Synch and Asynch Sequential Circuits

95 Introduction to Counters
Counters 的重点在于, 两个 JK flip flops 的 Clock 信号不同. 第二个 JK FF 的 Clock 为第一个的输出.
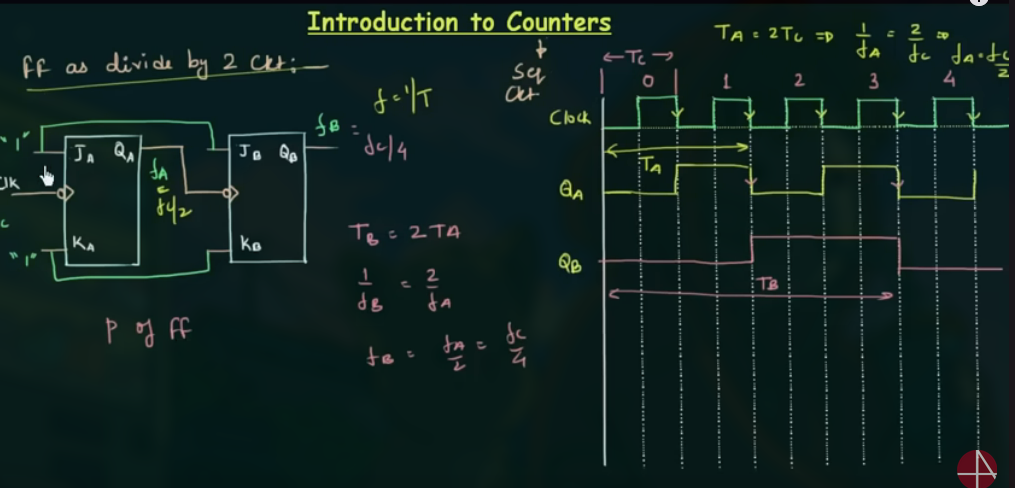
需要注意的是, 周期在不断 divide by 2.
output 的频率为:
$$
\displaylines
{
\begin{aligned}
f = \frac{f_c}{2^p}
\end{aligned}
}
$$
$f_c$ 是 clock 的频率, $p$ 是 flip flop 的个数.
这个示例 counter 是从 0 to 3:
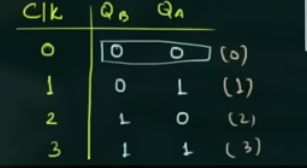
可以得出, 对于这种类型的 counter 若需要 $0 \sim 2^n-1$ 的 counter, 则需要 n 个 flip flop.
96 Types of Counters
有两种 counters:
- Asynchronous Counter
如:
- Synchronous Counter
如:
对比:

另一种分法:
- Up counters, 0,1,2,…
- Down counters, 7,6,5,…
- Up/Down counter
97 3 Bit Asynchronous Up Counter
3 bit 表示从 000 to 111 (0 to 7)
98 Introduction to Register
Flip Flop 是 1-bit memory cell.
Register 就是 a group of Flip Flop
4-bit 寄存器就应该包含 4 个 Flip Flop.
当电路为这样时:
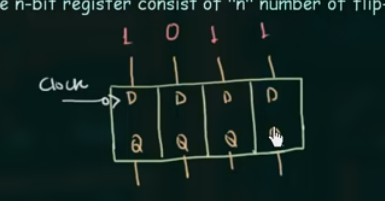
此时并不能真正存储数据, 因为每一位都在不停变动.
需要加入一个控制信号, 来控制数据的更新, 这个信号被称为 load:
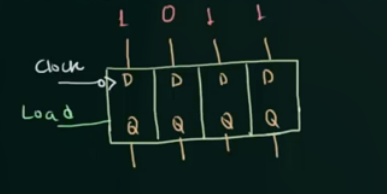
对于 Synch 和 Asynch 的 register, 的区别:
- Synch: clock 和 load 都为 high 时更新
- Asynch: 只有 load 为 high 时更新
99 Data Formats & Classification of Registers
Data 有两种输入形式:
- serial, one bit at a time
如:
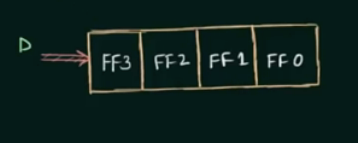
这里的 FF 为 Flip Flop
- parallel, all bits at a time
如:
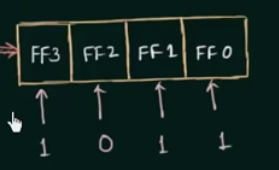
几种写法, 通过 input 和 output 的方式判断 register 类型:
- SISO, Serial in Serial out
- SIPO, Serial in Perellel out
- PISO, Perellel in Serial out
- PIPO, Perellel in Perellel out
通过应用分:
- Shift Register
- Storage Register
100 Shift Register (Serial In Serial Out)
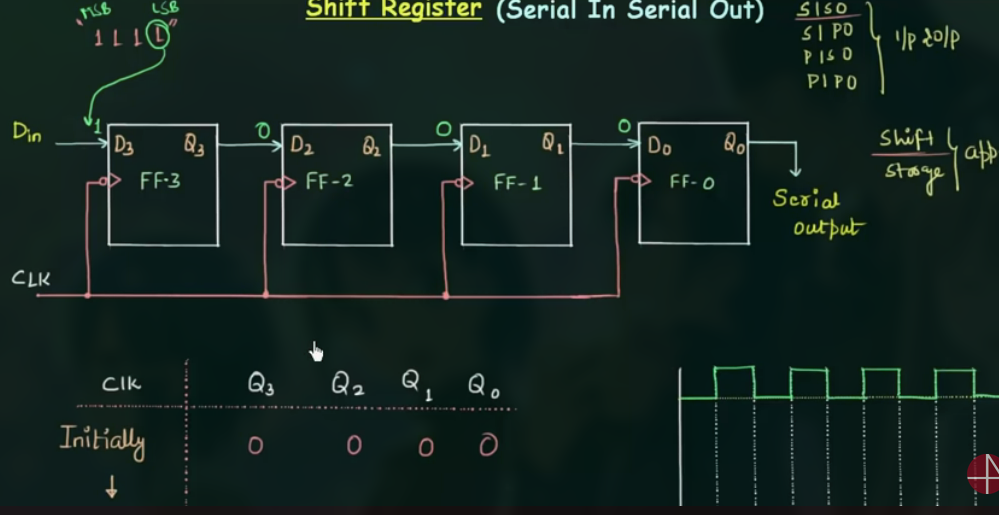
注意对 MSB, LSB 的标注.
这里变化的时间是时钟的下降沿.
状态变化和时序图:
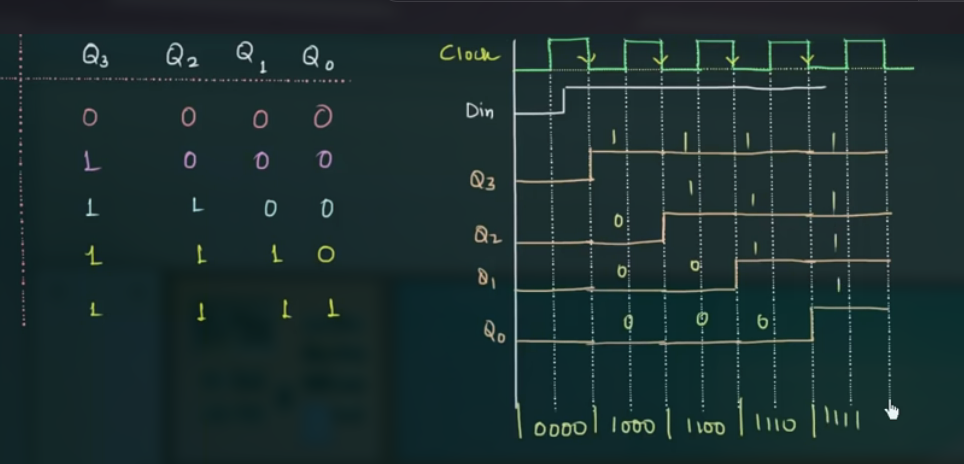
每一次移 1 位.
长距离用 SISO Shift Register 比较好:
如果用 parallel 则需要 20km 的线.
101 Shift Register (SIPO & PIPO Mode)
你要传几位, 就需要用几个时钟周期来存储. 取出也是同样.
对于 SIPO:
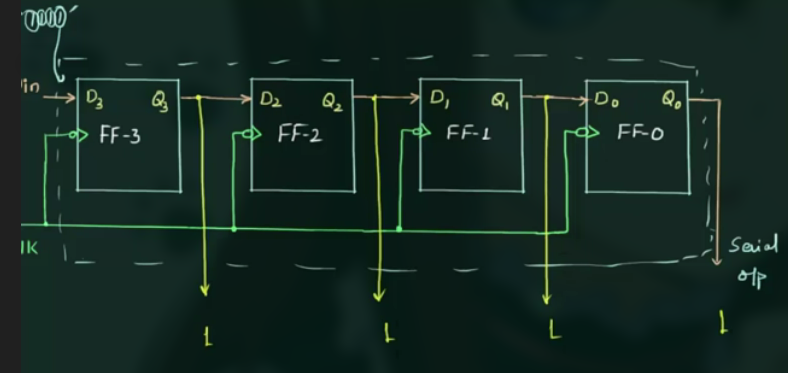
所有结果在一个始终周期传出.
- SISO, SIPO, 都需要 4 clock to store data
而 PIPO 被称为 Storage Register 或 Buffer Register
因为输入什么就等下输出什么.
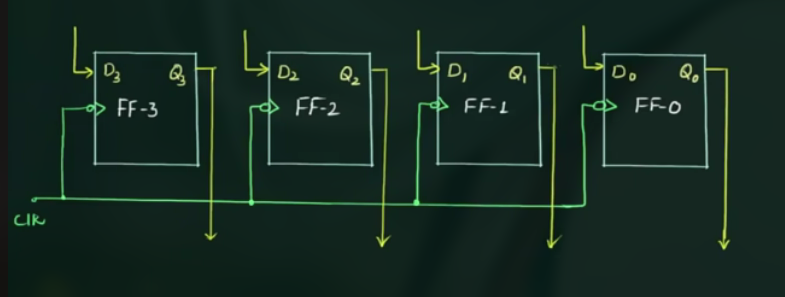
- PIPO, 1 clock to store data
102 Shift Register (PISO Mode)
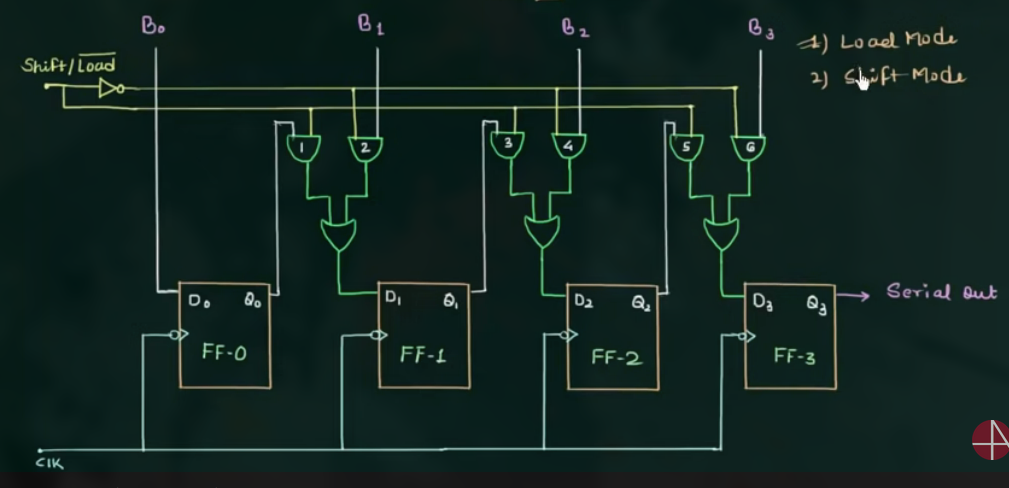
可以看到左上角的信号, 其决定:
- 0, Load Mode
如:
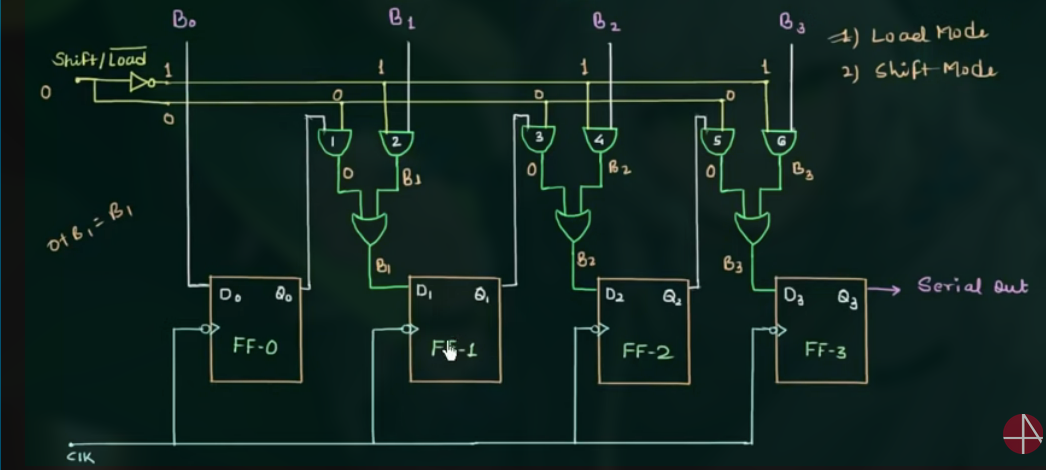
- 1, Shift Mode
如:
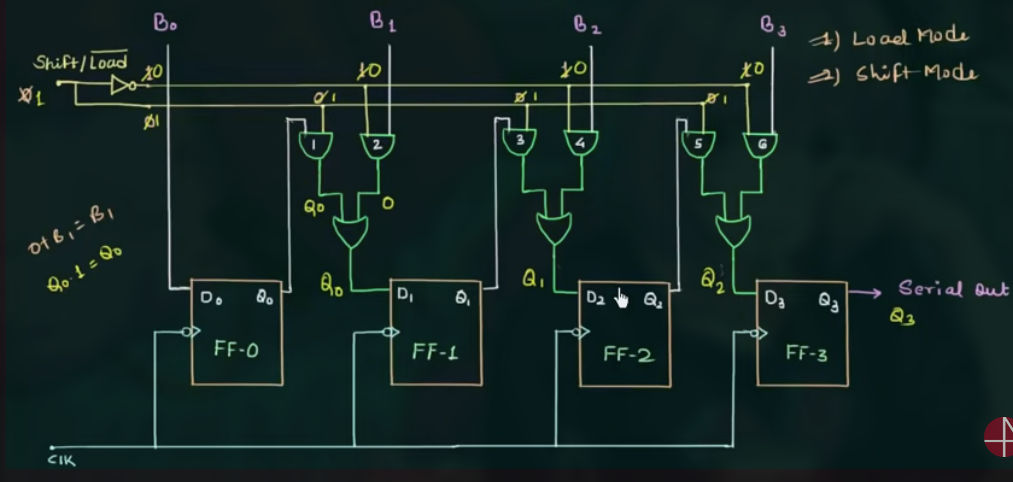
103 Bidirectional Shift Register
也就是可以向两个方向 shift 的 shift register
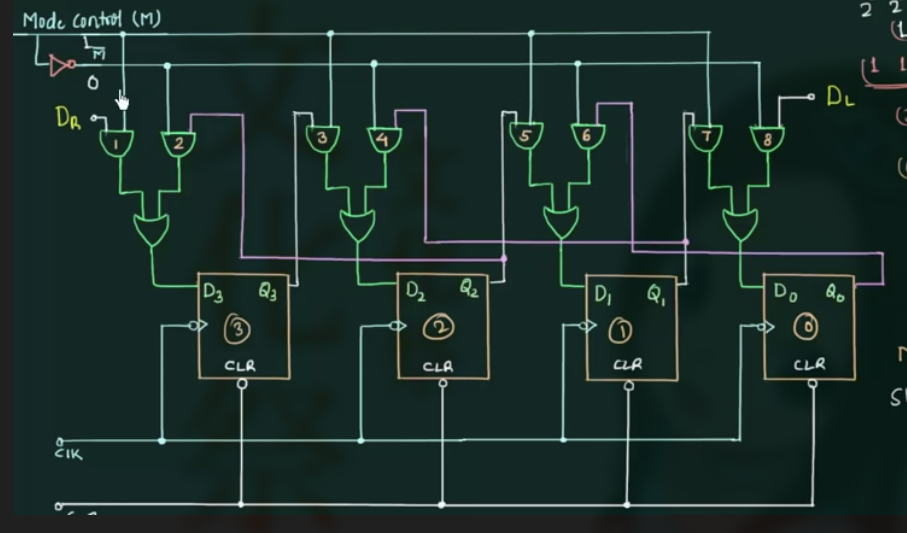
104 Universal Shift Register
Universal Shift Register = Bidirectional Shift Register + Parallel Loading
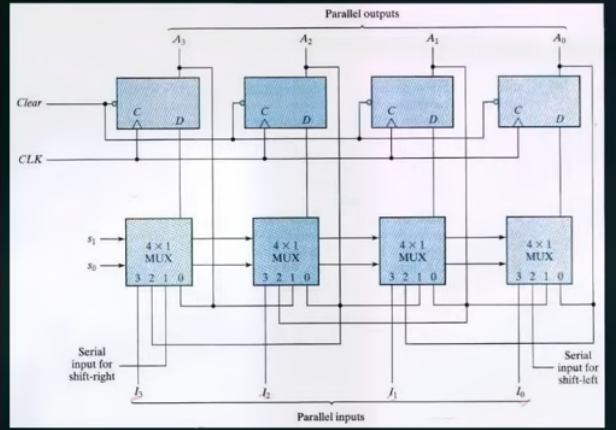
这里的 mux 用于 mode control.

105 Practise
填 K’Map 时注意 11 和 10 的顺序是相反的.
Problem1
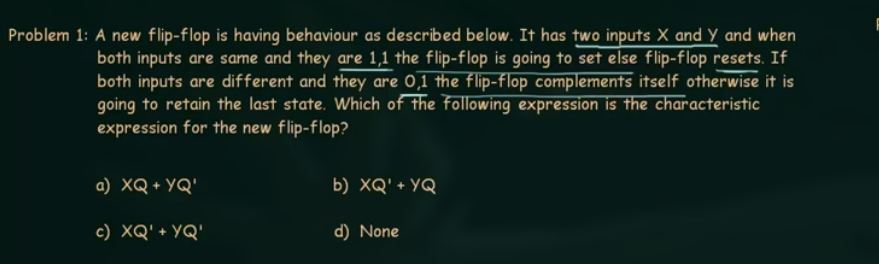
- 根据题干写出所有的 input 和 output 的真值表
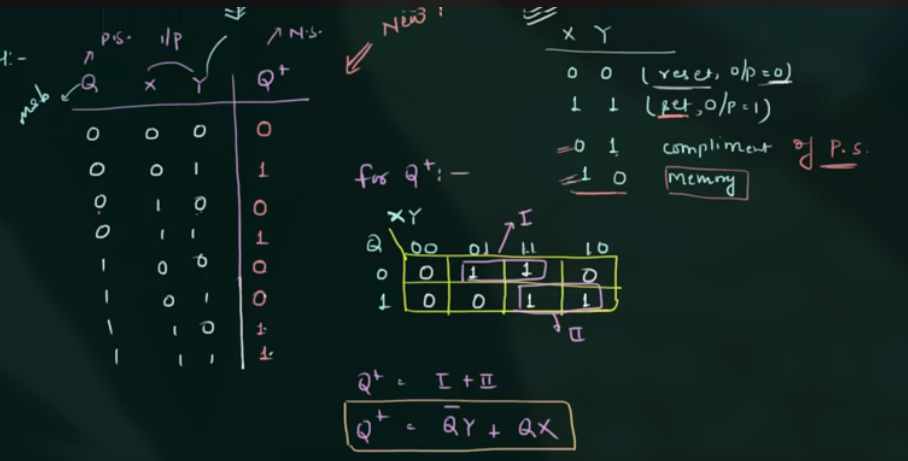
Problem2