微电子电路-第五版-Notes
第1章 电子学简介
第3章 二极管
最简单和最基本的非线性电路元件是二极管, 即流过其上的电流和它两端的电压具有非线性关系.
二极管也有两个连接端, 但没有电阻特性.
3.1 理想二极管
3.1.1 电流-电压特性
理想二极管的端口特性可以解释为:
- 如果将负电压加到二极管上, 那么二极管上将没有电流流过, 相当于开路, 此时称为 反向偏置或者反向工作
- 如果将正电流加到理想二极管上, 那么二极管两端电压降为0, 相当于短路, 此时称为 正向偏置
其电路图为:
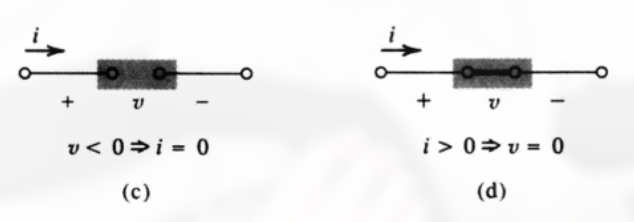
其伏安图为:
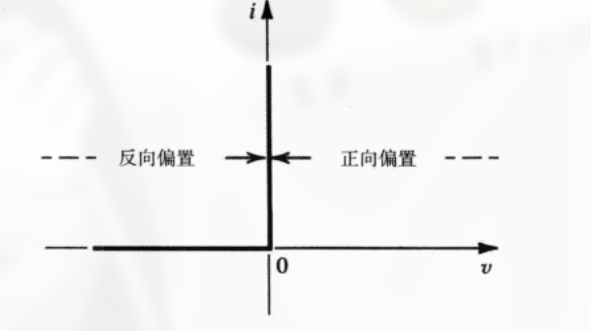
解释: 这里的 $v$ 指二极管两端电压, 在正向偏置时, 二极管相当于短路, 因此电压只为零, 因此可以看到正半轴没有画出, 而电压为 0 时有电流值; 而处于反向偏置时, 电压为负, 且电流为零, 可以看出, 负半轴有电压值, 且电流为零.
(也就是说, 二极管上的电压只有两种情况, 等于零或小于零)
从这幅图就可以看出为 非线性 .
对于二极管符号的解释 :
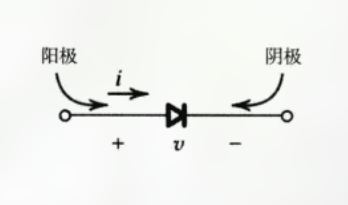
箭头符号表示电流能流过的方向.
3.1.2 一个简单应用 – 整流器
电路图如:
电路组成:
- 一个正弦电源
- 一个二极管
- 一个电阻
输入电压为:
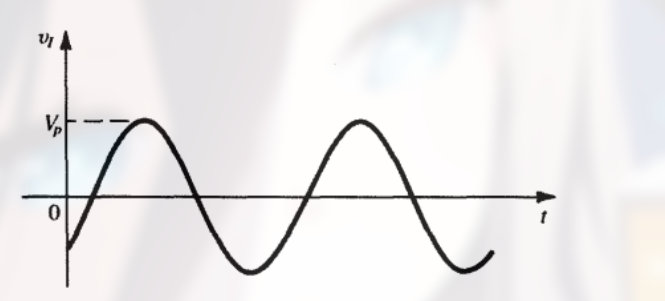
由于二极管的作用, 当电压为负时, 电流为零, 则输出电压为:
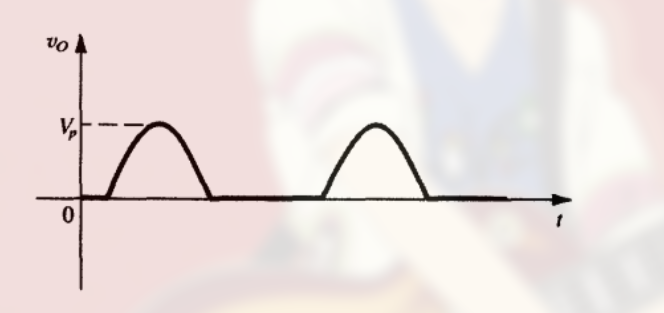
(毕竟此时相当于开路)
3.1.3 另一种应用 – 二极管逻辑门
两个对应概念:
- 电压值接近于 $0V$ 对应于逻辑 0 (低)
- 电压值接近于 $+5V$ 对应于逻辑 1 (高)
或门实现:
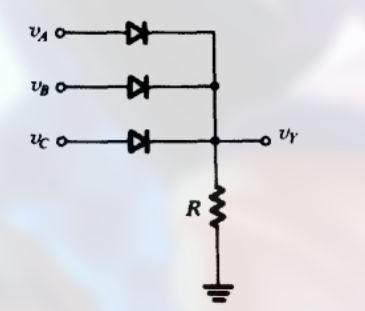
也就是说, 只要 $v_A, v_B, v_C$ 其中一个接入 $+5V$ 电压, 那么 $V_Y$ 则会导通.
布尔代数形式为:
$$
\displaylines
{
Y = A + B + C
}
$$
(只要 $A, B, C$ 中一个为 1, 则 Y 也为真)
与门 实现:
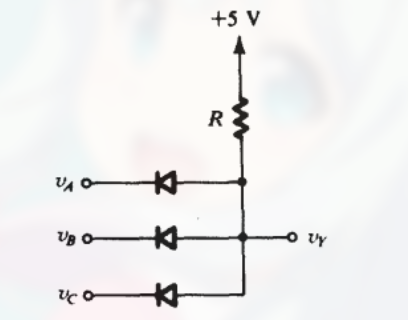
只要 $v_A, v_B, v_C$ 其中一个为 0, $V_Y$ 都不会被导通. (毕竟, 如果 $V_A$ 为0, 那么电流则会直接从 $V_A$ 端口流出)
布尔代数形式为:
$$
\displaylines
{
Y = A \cdot B \cdot C
}
$$
(只要 $A, B, C$ 中一个为 0, 则 Y 为假)
例题中,一般不可能 一眼就看出二极管是否导通, 需要做假设, 然后验证是否可以得到一致的结论, 如:
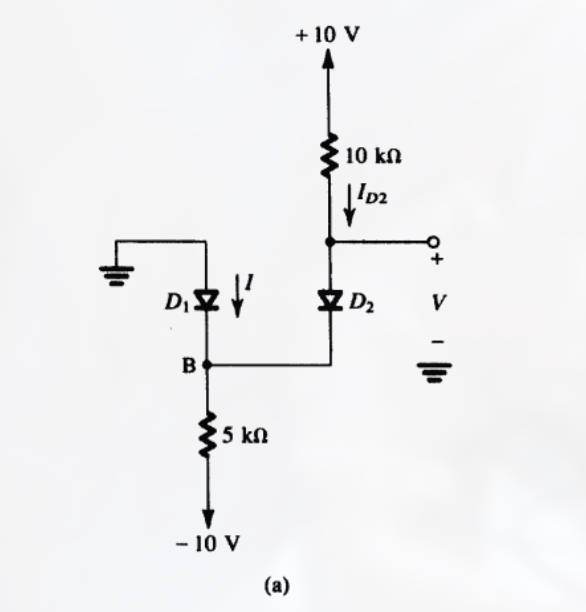
这里先假设两个二极管都导通, 然后验证.
3.2 结二极管端口特性
硅结二极管 (硅结的含义为, 硅被掺杂后形成的 PN 结) 的特性曲线由三个不同的部分组成:
- 正向偏置区域, $v>0$ 区域
- 反向偏置区域, $v<0$ 区域
- 击穿区, $v<-V_{ZK}$ 区域
(击穿的含义, 可能是指, 失去了二极管的性质, 在这里, 也就是相当于短路了)
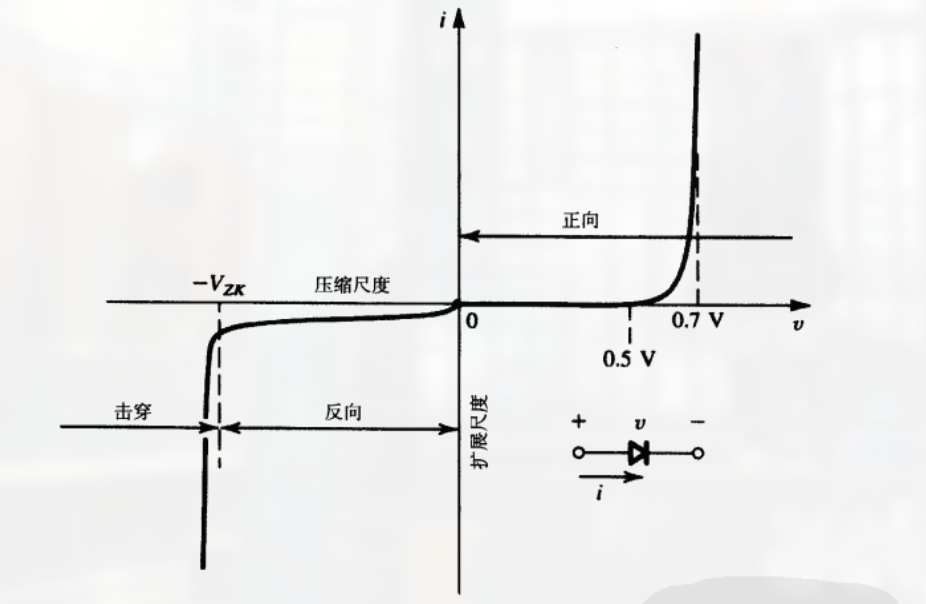
按理说在 $v = 0$ 处才会有电流, 但那是理想情况下, 这里的非理想二极管两端可以有 $0.7V$ 的压降.
在 $v<0$ 时, 按理说也不会有电流, 但在非理想的情况下, 在 $-V{ZK} \sim 0$ 间有少量电流, 且在电压降低于 $-V_{ZK}$ 时, 二极管被损坏 (被击穿), 因此失去二极管性质, 电路导通, 因此电流急剧增加 (就像短路一样).
3.2.1 正向偏置区域
此时, 电压变化极小部分, 而电流变化极快.
当端口电压为正时, 则进入正向偏置工作区域, 其伏安关系近似为:
$$
\displaylines
{
i = I_S (e^{v/nV_T} - 1)
}
$$
(也就是描述那段曲线, 非线性线段)
其中:
- $I_S$, 为饱和电流
其也叫做 比例电流 , 因为其大小与二极管的横截面积成正比. (结面积增大一倍将导致二极管的 $I_S$ 也增大一倍)
- $V_T$, 为热电压, 其是一个常数
$$
\displaylines
{
V_T = \frac{kT}{q} \approx 2.5 \times 10^{-3}
}
$$
其中:
$k$ 为玻尔兹曼常数, 值为 $1.38 \times 10^{-23}J/K$
$T$ 为热力学温度, 值为 $273$ 开氏温度.
$q$ 为电荷量, 值为 $1.60 \times 10^{-19}C$
- $n$ 是一个处于 1 和 2 之间的值, 其取决于二极管的材料和物理结构
一般情况下, $i >> I_S$, 因此原式可以近似为:
$$
\displaylines
{
i \approx I_S e^{v/nV_T} \newline~ \newline
v = nV_T \ln \frac{i}{I_S}
}
$$
二极管的一个特性推导
当电流有 10 倍变化时, 二极管的电压降将变化 $2.3 n V_T$ 倍:
$$
\displaylines
{
I_1 = I_S e^{V_1/nV_T} \newline~ \newline
I_2 = I_S e^{V_2/nV_T} \newline~ \newline
\frac{I_2}{I_1} = e^{(V_2 - V_1)/nV_T} \newline~ \newline
V_2 - V_1 = n V_T \ln \frac{I_2}{I_1} \newline~ \newline
= 2.3 n V_T \log \frac{I_2}{I_1}
}
$$
当 $n = 1$ 时, 大约变化 $60mV$, 当 $n = 2$ 时, 大约变化 $120mV$.
3.2.2 反向偏置区域
当二极管电压 $v$ 为负则进入 反向偏置工作区 .
其曲线同样由下列式子描述, 只不过此时 $v<0$:
$$
\displaylines
{
i = I_S (e^{v/nV_T} - 1)
}
$$
以及 $v >> V_T$ 可知:
$$
\displaylines
{
i \approx -I_S
}
$$
( 如 $e^{-\infty} = 0$, 那么 $e^{-\infty} - 1 = -1$ )
此时的电流称为 $反向电流$, 其为常数 $I_S$ (这里就是饱和电流的由来)
3.2.3 击穿区域
当反向电压的幅值超过特定二极管指定的门限电压时就进入击穿区域, 该门限称为 击穿电压 .
在击穿区域, 反向电流快速增大, 而相关的电压降增加非常小.

3.3 二极管正向特性建模
3.3.1 指数模型
3.3.8 小信号模型
这个模型同样是为了求得流过二极管两端电流和电压的关系, 只不过, 此时多了一个交流小信号. 因此, 从求:
$$
\displaylines
{
I_D 和 V_D
}
$$
变为求:
$$
\displaylines
{
I_D + i_d 和 V_D + v_d
}
$$
其只能对小信号适用的原因是, 要求得 $i_d$ 和 $v_d$, 则需要利用 $r_d$ 和欧姆定理, 而欧姆定理只能在线性电路中使用, 当信号足够小时, 可以将其近似为线性的 (就像微积分, 实际上是靠后面的幂级数展开), 因此就可以求得 $i_d$ 和 $v_d$.
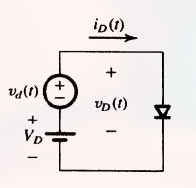
直流电压为 $V_D$, 时变信号为 $v_d(t)$.
当没有 $v_d(t)$ 信号时, 有:
$$
\displaylines
{
I_D = I_S e^{V_D/nV_T}
}
$$
($I_D$, $I_S$ 和 $V_T$ 的定义可看前面)
加上 $v_d(t)$ 时, 总的电源瞬时电压 $v_D(t)$ 为:
$$
\displaylines
{
v_D(t) = V_D + v_d(t)
}
$$
因此, 总的瞬时电流 $i_D (t)$ 为:
$$
\displaylines
{
i_D (t) = I_S e^{(V_D + v_d)/nV_T} \newline~ \newline
= I_S e^{V_D/nV_T} e^{v_d/nV_T}
}
$$
由于: $I_S e^{V_D/nV_T}$ 可以写为 $I_D$, 因此有:
$$
\displaylines
{
i_D(t) = I_D e^{v_d/nV_T}
}
$$
由幂级数展开式:
$$
\displaylines
{
e^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + …
}
$$
可得:
$$
\displaylines
{
i_D(t) = I_D [ 1 + \frac{v_d}{nV_T} + ( \frac{v_d}{nV_T} )^2 \frac{1}{2!} + … ]
}
$$
当 $v_d(t)$ 足够小时, 有:
$$
\displaylines
{
\frac{v_d}{nV_T} \ll 1
}
$$
因此, 指数展开式的第二项以后的级数都可以忽略.
有:
$$
\displaylines
{
i_D(t) = I_D [ 1 + \frac{v_d}{nV_T} ]
}
$$
这个近似就称为 小信号近似. 当 $n = 2$ 且信号幅度小于 $10mV$ 时, 或 $n = 1$ 且信号幅度小于 $5mV$ 时, 这个近似是有效的.
最终有:
$$
\displaylines
{
i_D(t) = I_D + \frac{I_D}{nV_T} v_d \newline~ \newline
i_D = I_D + i_d \newline~ \newline
其中, i_d = \frac{I_D}{nV_T} v_d
}
$$
同时能得到 二极管小信号电阻值 (增量电阻, 等效于二极管两端增加的电阻) 为:
$$
\displaylines
{
r_d = \frac{nV_T}{I_D}
}
$$
(由 $i = \frac{V}{R}$ 以及上面的 $i_d = \frac{I_D}{nV_T} v_d$ 可得到)
一个特点
伏安曲线在 $i = I_D$ 处的斜率等于 $I_D / nV_T$ 也就是 $1/r_d$
具体的解题思路
- 求直流信号的电压和电流
- 求增量电阻 $r_d$
- 求时变电流 (或时变电压, 看已知的是哪个)
- 相加
3.3.9 二极管正向压降在稳压器中的应用
稳压器 的目的就是在其输出端提供固定的直流电压. 无论是从稳压器输出端得到的负载电流发生变化, 还是输入稳压器电路的直流电源电压发生变化, 都要求输出电压尽可能地保持不变.
因为二极管的正向电压降几乎保持在 $0.7V$ 左右, 而流过它的电流相对来说可以有比较大的变化, 因此一个正向偏置的二极管可以被构造成一个简单的稳压器 (也就是说, 和二极管并联的负载, 可以得到几乎不变的压降, 比如和一个二极管并联, 压降会保持在 $0.7V$, 和两个串联的二极管并联, 压降会保持在 $1.4V$, 以此类推 )
解题思路
一般是求电源电压发生如 $\pm 1%$ 变化时, 求稳压器电压发生的变化.
这里电源电压发生的变化, 就相当于是小信号. 就可以用小信号模型来解.
稳压器电压发生变化的原因, 就是由于小信号产生了增量电阻, 因此负载的分压发生了变化.
如:
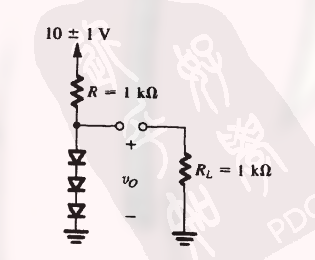
$$
\displaylines
{
\Delta v_O = 2 \frac{r}{r+R}
}
$$
(这里的 2 是由于 $\pm$ 引起的)
求, 当加上负载电阻时, 稳压器电压变化. 此时不再是小信号模型. 如:

3.4 工作在反向击穿区域的二极管 – 齐纳二极管
二极管在 击穿区域 具有非常陡峭的伏安曲线和 几乎不变的电压降 , 这个表明工作在击穿区域的二极管可以设计成稳压器.
制作出的, 专门工作在击穿区域的二极管, 称为 击穿二极管 , 或 齐纳二极管 (科学家名字命名).
其符号为:
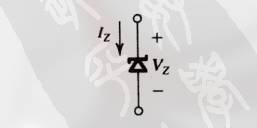
3.4.1 齐纳二极管的规范和建模
二极管的伏安特性图:
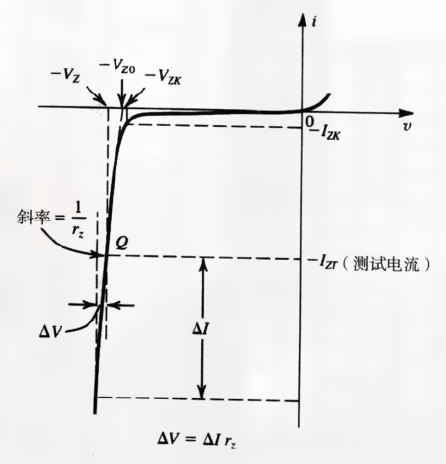
注意几个量:
- $V_Z$: 额定电压
- $I_{ZT}$: 测试电流
- $V_{ZO}$: 线性方程和 x 轴的交点
- $V_{ZK}$: 击穿电压 (拐点电压)
- $I_{ZK}$: 击穿电压下的电流 (拐点电流)
对于电流变化 $\Delta I$, 齐纳电压的变化为 $\Delta V$, 有:
$$
\displaylines
{
\Delta V = r_z \Delta I
}
$$
(下标 z 指 zener)
其中, $r_z$ 是几乎呈线性的伏安曲线在 Q 点的斜率的倒数, 也就是齐纳二极管工作在点 Q 的 增量电阻 , 也称为齐纳二极管的 动态电阻 .
一般来说, $r_z$ 的值在几个欧姆到几十个欧姆的范围内.
$r_z$ 值越小, 电流变化时齐纳电压就越稳定. (毕竟 $r_z$ 是斜率的倒数, 其值越小, 斜率就越大, 电流变化增快的同时, 电压变化变慢)
齐纳二极管几乎呈线性的伏安特性表明, 能建立如下的模型:
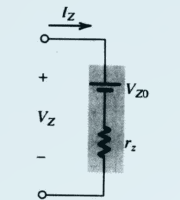
(将二极管拆分为电阻和电源的串联)
$V_{z0}$ 为斜率为 $1/r_z$ 直线与电压轴相交的点.
尽管 $V_{Z0}$ 与拐点电压 $V_{ZK}$ 有些不同, 其值几乎相等.
因此上面的模型可以描述为:
$$
\displaylines
{
V_Z = V_{Z0} + r_z I_Z
}
$$
其适用于 $I_Z > I_{ZK}$ 时.
3.4.2 作为并联稳压器的齐纳二极管
这里的并联稳压器也叫做 分流稳压器 (毕竟并联分流)
例题如:
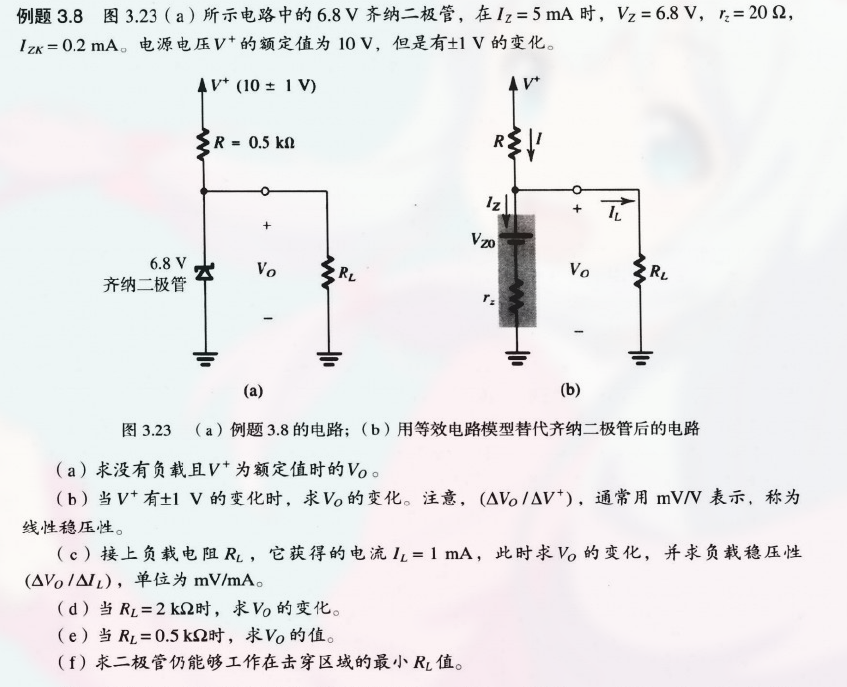
3.4.3 温度效应
齐纳电压 $V_Z$ 与温度的相关性由它的温度系数 TC (temco) 来指明 (单位为 mV/C).
TC 的值取决于齐纳电压, 对于一个给定的二极管, TC 随工作电流变化:
- $V_Z$ 低于 5 V 的齐纳二极管呈负的温度系数现
- $V_Z$ 约为 5 V 的齐纳二极管 温度系数可能为 0
- $V_Z$ 高于 5 V 的齐纳二极管呈 正的温度系数
例题:

这种题的关键在于, $r_z = 50$, 可以得到斜率的大小, $10mA, 10V$ 是直线上的一点. 因此可以得到线性方程.
$$
\displaylines
{
y = ax + b,\ \ a = \frac{1}{r_z} = \frac{1}{50} \newline~ \newline
10 \times 10^{-3} = \frac{1}{50} \times 10 + b \newline~ \newline
b = -0.19 \newline~ \newline
当I = 5mA \newline~ \newline
有: 5 \times 10^{-3} = \frac{1}{50} x - 0.19 \newline~ \newline
x = 9.75V
}
$$
另外的例题:

(还不是很明白)
3.5 整流电路
二极管整流器是电源电子设备中直流电源的一个重要构建, 如:
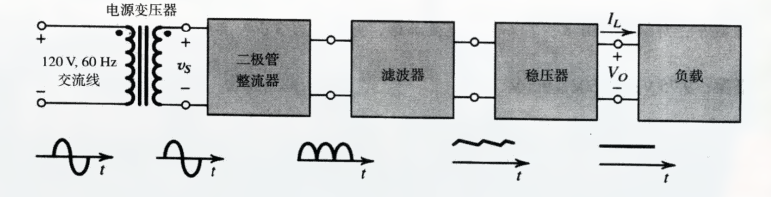
除了为直流电源提供合适的正弦信号的幅度之外, 电源变压器还为电子设备和电源线电路之间提供电隔离.
二极管整流器将输入正弦波 $v_s$ 转换为单极性输出. (也就是上图中的波形图)
3.5.1 半波整流器
半波整流器工作在输入正弦波交替的半个周期内.
其电路为:
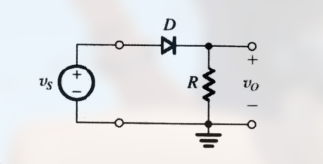
可以等效为:
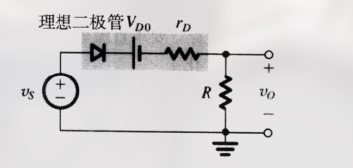
有:
$$
\displaylines
{
v_O = 0, \ v_S < V_{D0} \newline~ \newline
v_O = \frac{R}{R + r_D} v_S - V_{D0} \frac{R}{R + r_D},\ v_S \ge V_{D0}
}
$$
(这里相当于两个电压源, 利用叠加原理写出)
当 $r_D \ll R$ 时, 有:
$$
\displaylines
{
v_O \approx v_S - V_{D0}
}
$$
由于, 在 $v_o=0$ 时 (即整流的过程), 二极管处于反向电压区域, 因此二极管能承受的击穿反向电压需要比此时的电压大. (谨慎些的话, 二极管的反向击穿电压至少比期望的 PIV 大 50%, PIV 指反向峰值电压, Peak Inverse Voltage)
解释最开始说的工作周期:
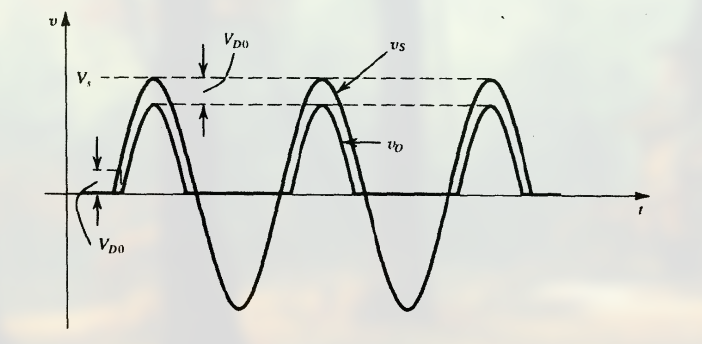
可以看出, 只有在输入电压 $v<0$ 时整流器才工作.
3.5.2 全波整流器
全波整流器工作在输入正弦波的两个半周期内. 其将 正弦波的负半周反转
如:
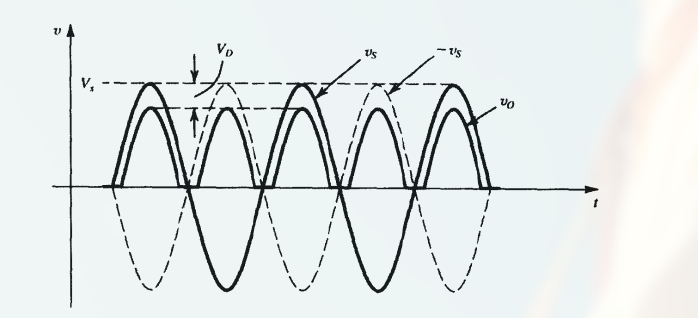
其电路图实现可以为:
解释
这里有两个二极管( $D_1,D_2$ ):
- 当交流线电压为正半周时 (即输入信号为正), $D_1$ 导通, $D_2$ 反向偏置 (此时电流为顺时针), 流过 $D_1$ 的电流将流过 R.
- 当交流线电压为负半周时 (即输入信号为负), $D_1$ 截止, $D_2$ 导通 (此时电流为逆时针), 流过 $D_2$ 的电流将流过 R.
这里的 中心抽头 指的是指一个点,它位于输入交流电源的两个端子之间,并连接到一个二极管桥的两个输入端之一。中心抽头的作用是将输入信号分成两半,每一半被分别整流,然后再将两半信号的输出合并成一个输出信号。
(不是很理解这句话)
注意 , 上述两种情况中, 流经 R 的电流总是以相同的方向流过, 因此 $v_O$ 是单极性的.
由于全波整流器可以产生比半波整流器具有更大能量的波形 (?) 因此在几乎所有的整流器应用中都会选择全波整流器类型.
其 PIV 为:
$$
\displaylines
{
PIV = v_O + v_s \newline~ \newline
= v_s - v_D + v_s \newline~ \newline
= 2v_s - v_D
}
$$
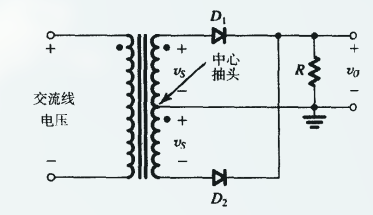
3.5.3 桥式整流器
叫这个名称是由于其结构与惠斯通电桥类似, 如:
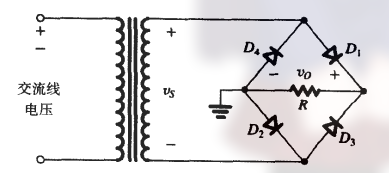
其需要 4 个二极管.
其工作原理如:
- 在 输入电压的正半周期 , $v_s$ 为正, 因此电流流过二极管 $D_1$, 电阻 R 和二极管 $D_2$, 此时二极管 $D_3$ 和 $D_4$ 反向偏置, $v_o = v_s - 2v_D$ (毕竟有两个二极管产生压降)
- 在 输入电压的负半周期 , $v_s$ 为负, 因此电流流过二极管 $D_3$, 电阻 R 和二极管 $D_4$, 此时二极管 $D_1$ 和 $D_2$ 反向偏置, $v_o = v_s - 2v_D$ (毕竟有两个二极管产生压降)
同样, 在两个半周期中 , 流过 R 的电流方向相同.
其 PIV 为 (考虑正半周期):
$$
\displaylines
{
v_{D3} (反向) = v_O + V_{D2} (正向) \newline~ \newline
PIV = v_s - 2v_D + v_D = v_s - v_D
}
$$
3.5.4 带滤波电容的整流器 – 峰值整流器
其电路为:
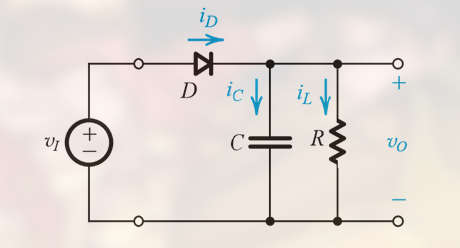
其在二极管和电阻串联的电路的基础上并联了一个电容器.
这里的二极管同样扮演半波整流器的作用, 去除掉了信号中的负半周期部分, 如:
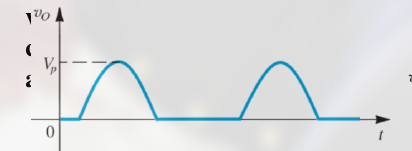
当输入信号处于正半周期时, 电容器充电; 当信号输入处于负半周期时, 电容器放电 (因为此时电路中每电流)
3.5.5 精密半波整流器 – 超二极管
3.6 限幅电路与钳位电路
3.6.1 限幅电路
限幅, 指的是限制输入信号的幅值. 其提供与输入成正比的输出, 即 $v_O = K v_1$
通过 K 的大小可以分为两种:
- $K > 1$, 有源限幅器
- $K \le 1$, 无源限幅器
(和有源, 无源滤波器中含义相同, 就是看有没有放大器)
被限制后的波形如:
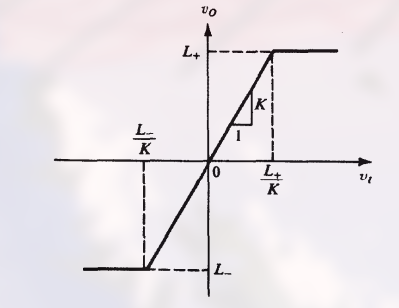
$\frac{L_+}{K}$ 被称为 上门限 , $L_+$ 被称为 上限电平 . 如果输出电压超过这个值, 就会被 限制或钳制 在 $L_+$ 处.
$\frac{L_-}{K}$ 被称为 下门限 , $L_-$ 被称为 下限电平 . 如果输出电压低于这个值, 就会被 限制或钳制 在 $L_-$ 处.
结合波形图来看:
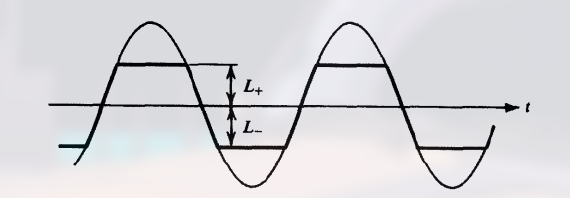
二极管和电阻相结合可以简单地实现限幅器的功能 :
如:
正半周期的单向限幅器
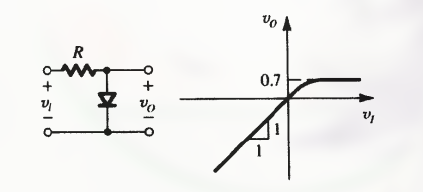
此时, 输出电压为 二极管两端电压 , 当:
- $v_i < 0.5V$, 二极管截止, 没有电流通过, 电阻 R 两端的电压降为 0, 此时 $v_o = v_i$ (为什么 0.5 V 为分界点)
- $v_i > 0.5V$, 二极管导通, 有电流通过, 二极管两端电压最高为 0.7V, 因此 $v_o$ 将被限制在一个二极管压降 (0.7V) 上
负半周期的单向限幅器
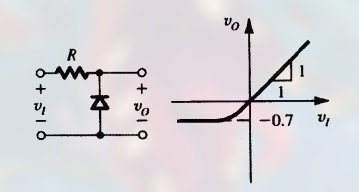
注意其二极管方向反向.
此时, 输出电压为 二极管两端电压 , 当:
- $v_i > -0.5V$, 二极管截止, 没有电流通过, 电阻 R 两端的电压降为 0, 此时 $v_o = v_i$
- $v_i < -0.5V$, 二极管导通, 有电流通过, 二极管两端电压最低为 -0.7V, 因此 $v_o$ 将被限制在一个二极管压降 (-0.7V) 上
双向限幅器
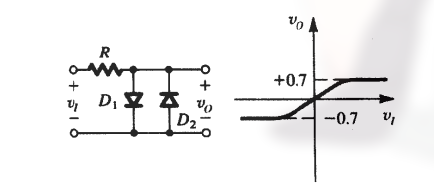
其并联两个极性相反的二极管.
此时,
- $-0.5V \le v_1 \le 0.5V$ 时, 两个二极管都截止, $v_o = v_i$
- $v_i > 0.5V$, $D_1$ 导通, $v_o$ 限制在 $+0.7V$
- $v_i < 0.5V$, $D_2$ 导通, $v_o$ 限制在 $-0.7V$
修改二极管限幅器的 门限与饱和电平
通过将二极管和直流电压串联来改变:
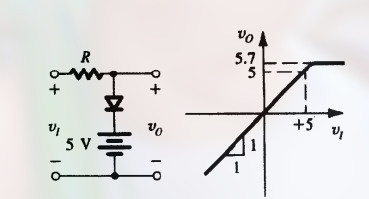
这里加的直流电源和输出电压方向一致, 因此是直接加 $5V$.
齐纳二极管限幅器
通过串联两个齐纳二极管来实现双向限幅:
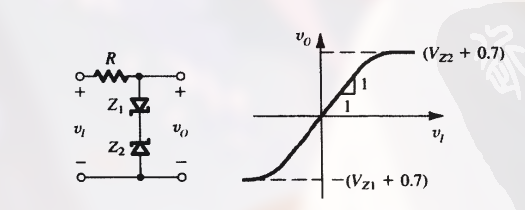
3.6.2 钳位电容或直流恢复器
钳位电容 指限制输出波形的最低值为某个特定值.
如:
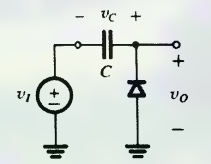
这里的输出电压为二极管两端电压.
输入信号为一个方波:
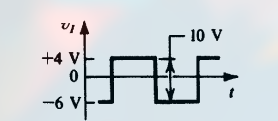
- 当处于负半周期时, 二极管导通 (考虑为理想二极管), 电容充电, 电容电压 $v_C = 6V$. 此时输出电压为 0 (毕竟二极管此时相当于导线)
- 当处于正半周期时, 二极管截止, 其两端电压为电源电压, 且电容放电, 因此输出电压为 $v_o = v_i + v_C = 10V$
因此, 输出的信号为 $0V \sim 10V$ 的方波:

由于输出波形的最低值被 钳位到 0V , 因此该电路也称为 钳位电容.
直流恢复器 指为失去直流分量的信号添加直流分量.
(具体暂时不清楚)
3.6.3 电压倍增器
即输出电压是输入峰值的倍数.
如:
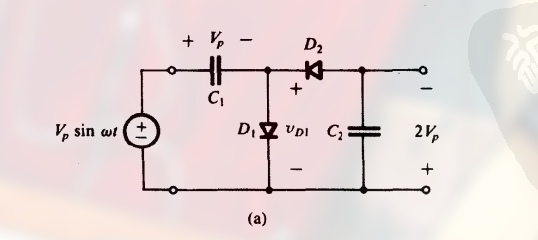
该电路由两部分级联而成:
- $C_1$ 和 $D_1$ 组成的钳位电路
- $D_2$ 和 $C_2$ 组成的峰值整流电路
有:
- 当输入信号为正半周期时, 电容器充电 ( $v_C = V_p$ ), 此时二极管导通 (由于是理想二极管, 此时相当于导线), $D_2$ 和 $C_2$ 此时组成的电路的输入电压为 0.
- 当输入信号为负半周期时, 电容器放电 ( 同样 $v_C = V_p$ ), 此时二极管截止 (两端电压为电源电压), 因此 $D_2$ 和 $C_2$ 此时组成的电路的输入电压为 $v_D + v_C = 2V_p$.
因此 $C_1$ 和 $D_1$ 组成的钳位电路的输出为:
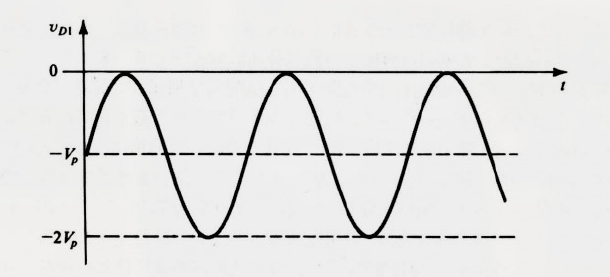
第4章 MOS 场效晶体管 (MOSFET)
这里讨论三端半导体器件. (之前的结二极管是二端半导体器件)
这里涉及的基本原理是: 利用两端之间的电压来控制流过第三端的电流.
因此, 一个三端器件可以用来实现一个受控源.
也可以使用控制信号使第三端电流从 0 变到一个较大的值, 作为 开关 工作.
三端半导体器件主要有两类:
- 金属-氧化物-半导体场效应管 (MOSFET)
- 双极型晶体管 (BJT)
与 BJT 相比, MOSFET 可以造得更小, 制造工艺相对比较简单, 且运行时需要的功率相对较低.
可以只使用 MOSFET 来实现数字电路和模拟电路. (不需要电阻或只需要少量电阻)
模拟功能和数字功能越来越多地在同一块 IC 芯片上实现, 这称为 混合信号设计
Youtube 介绍
其实体图如:

MOSFET 也可以分为 p-type 和 n-type
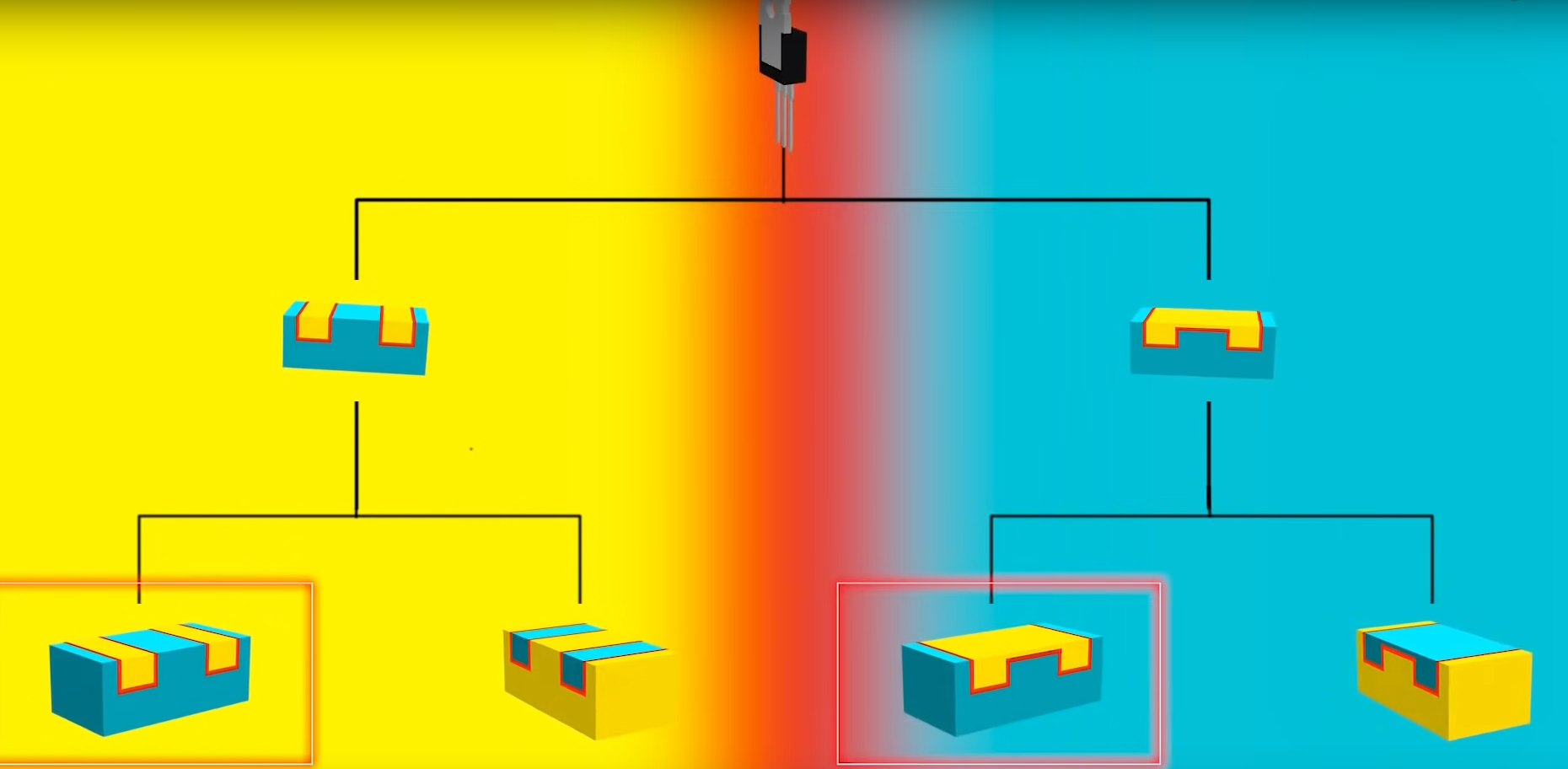
源极和漏极其实结构一样, 因此可以互换, 我们只是用谁连接电源的某个极来判断而已:
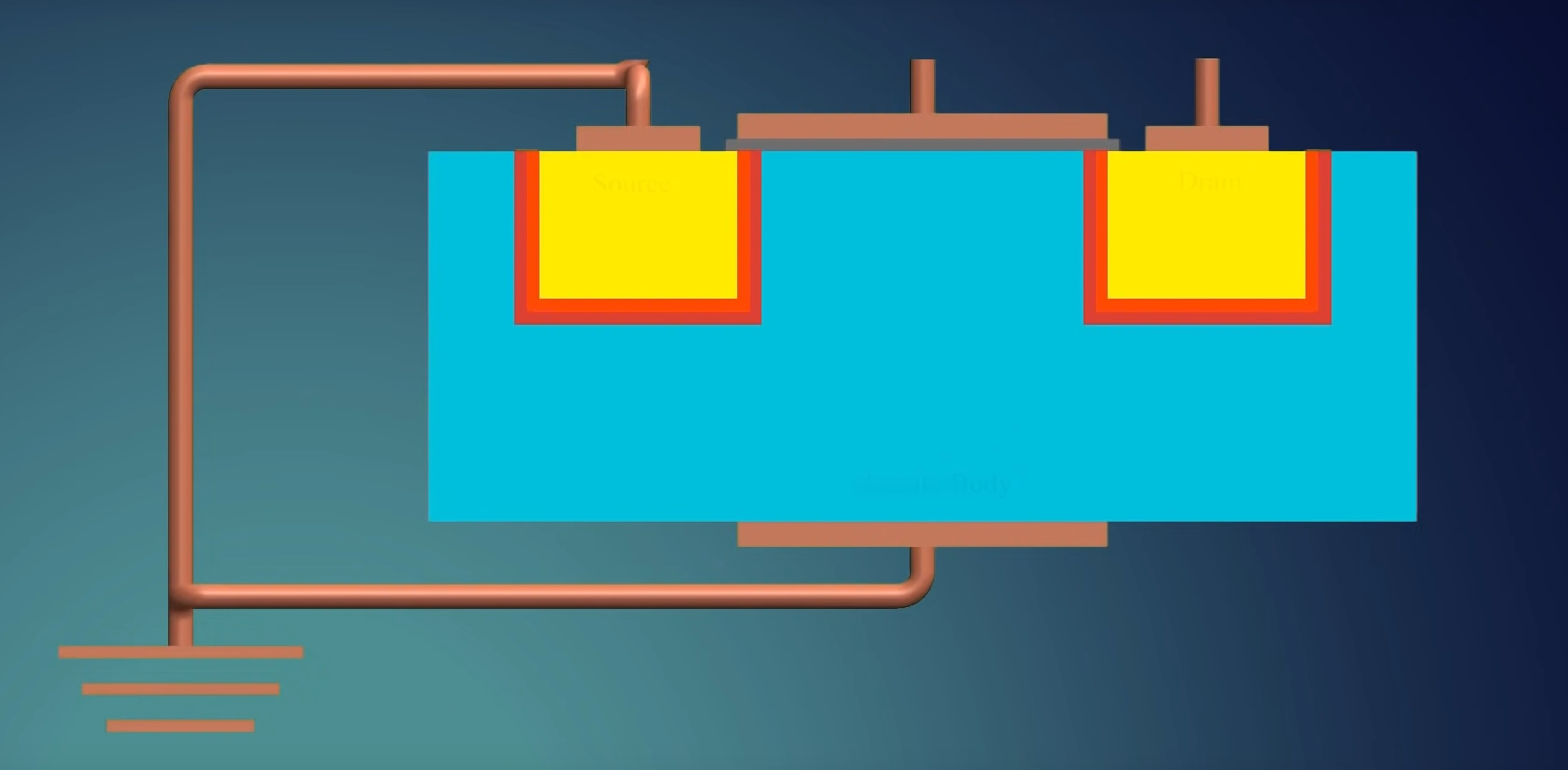
如添加一个 $V_{DS}$:
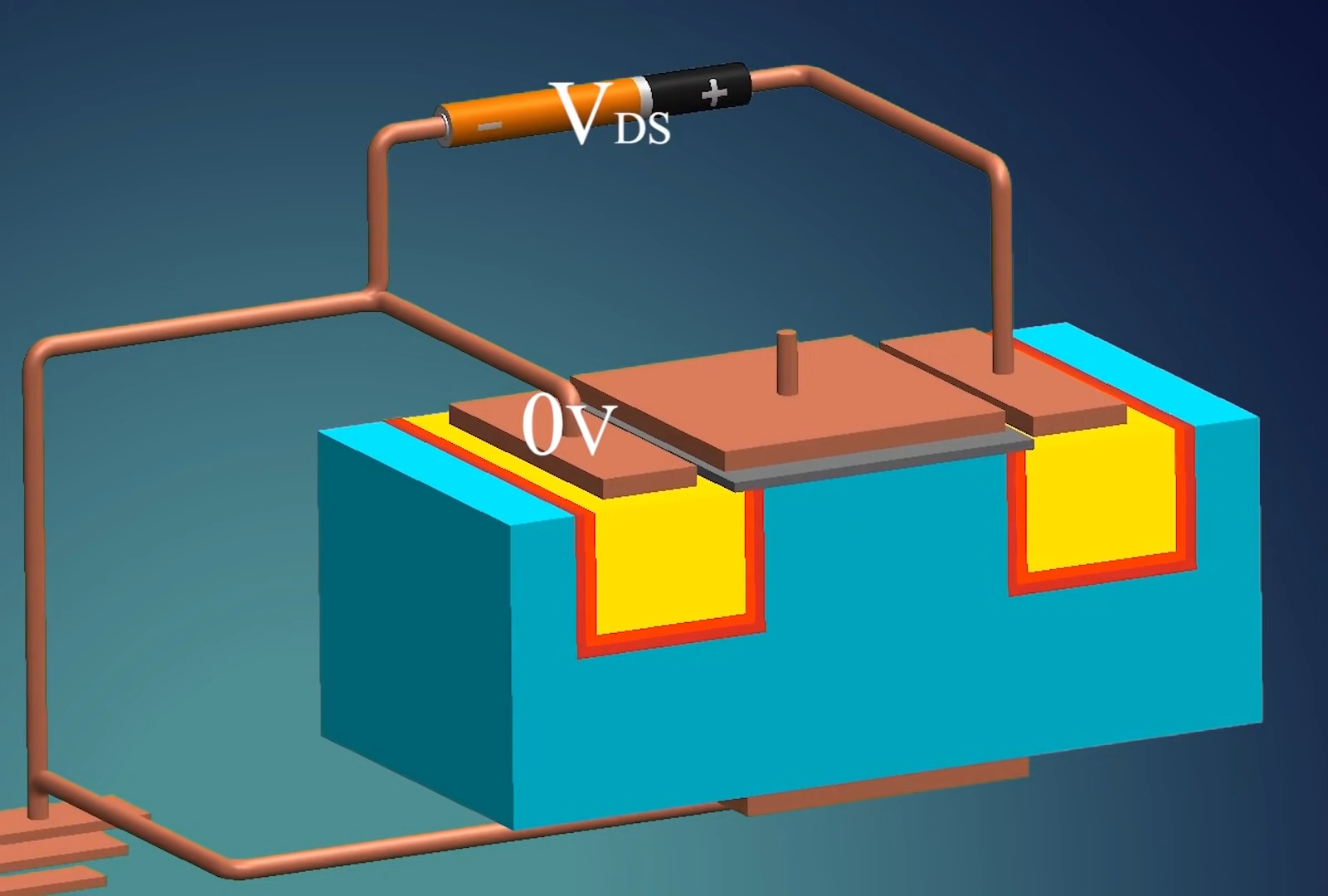
$V_{DS}$ 中的 DS 指电流方向, 从漏极 (Drain) 到源极 (Source).
此时增大 $V_{DS}$, 会使得漏极的耗尽层变小 (正向偏置电压)
但是电流无法从漏极流向源极. 需要创建一个 channel (沟道), 如添加一个 $V_{GS}$:
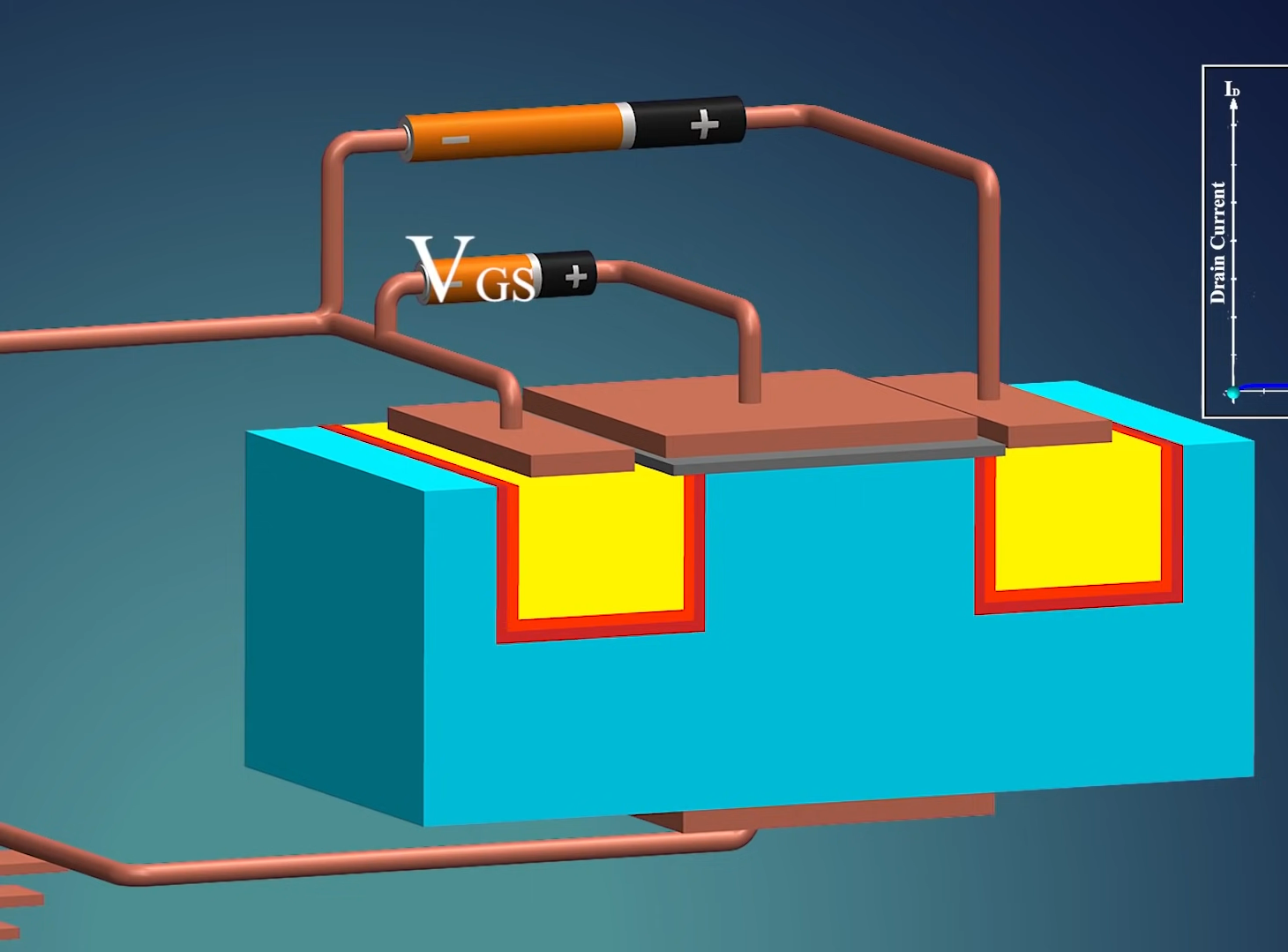
栅极之下为 p-type 区域, 但同样有自由电子, 在增加 $V_{GS}$ 的值时, 自由电子被吸引, 导致这片区域的空穴被填充, 同时, 也有空穴被排斥向下:
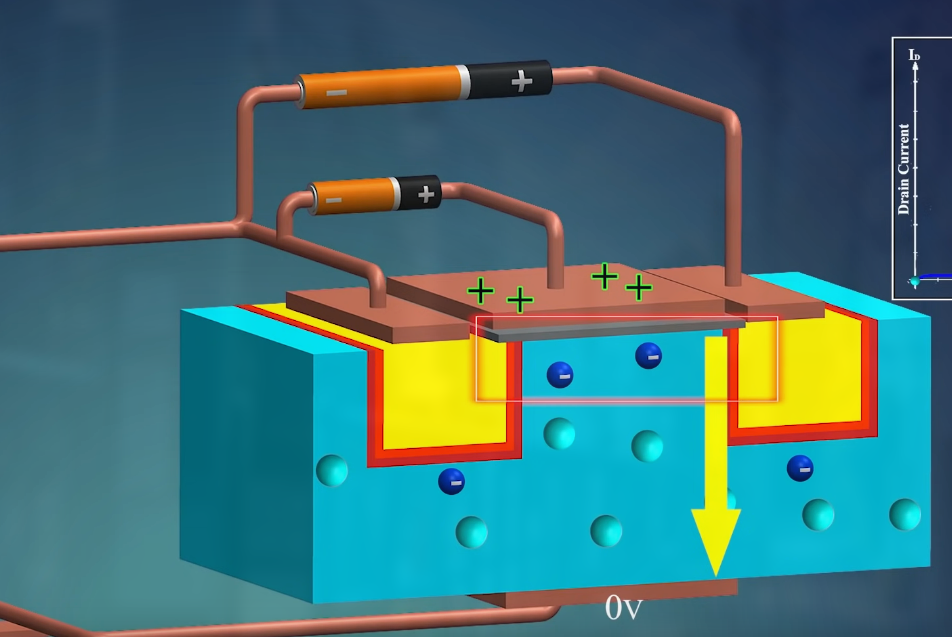
最终导致栅极之下的这片区域也变成 n-type, 也就形成了 channel:

能够使 channel 形成的 $V_{GS}$ 大小被称为 fresh voltage.
这个 channel 的宽度和 $V_{GS}$ 有关:
- $V{GS}$ 增大, channel 变宽
- $V{GS}$ 减小, channel 变窄
此时漏极和源极就被连通了. 电子可以沿这个通道流动:
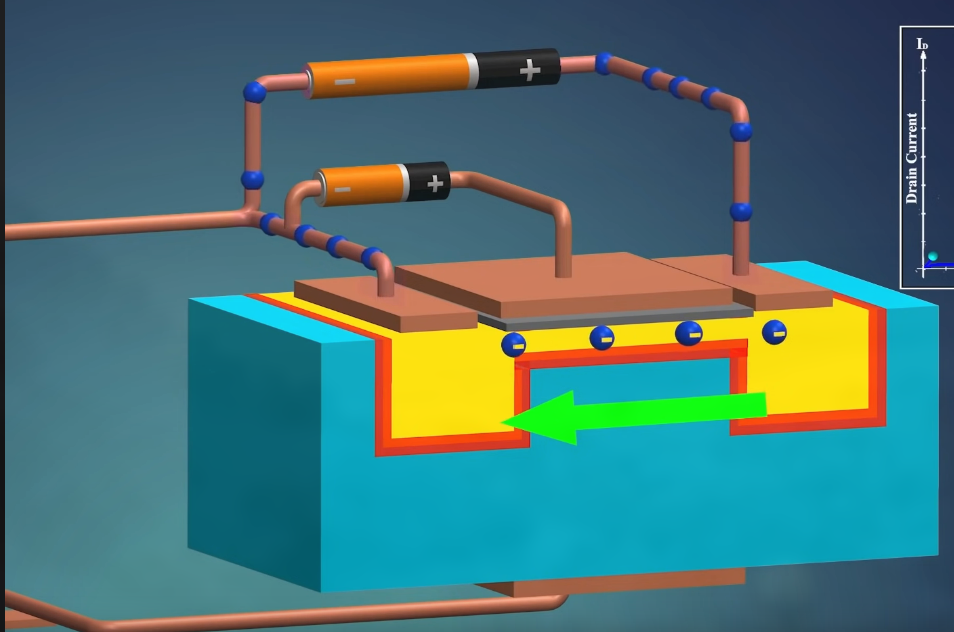
由于电流方向是从 Drain 到 Source, 因此这个电流被称为 Drain current.
由于栅极电压能控制 channel 的宽度, 因此其也能控制 Drain current 的大小.
4.1 器件结构与物理特性
4.1.1 器件结构
这里的示意图为 n 沟道增强型 MOSFET (n 沟道指沟道的类型为 n-type, 增强型指 $V_{GS}$ 增大会使沟道增强, 这些后面会解释):
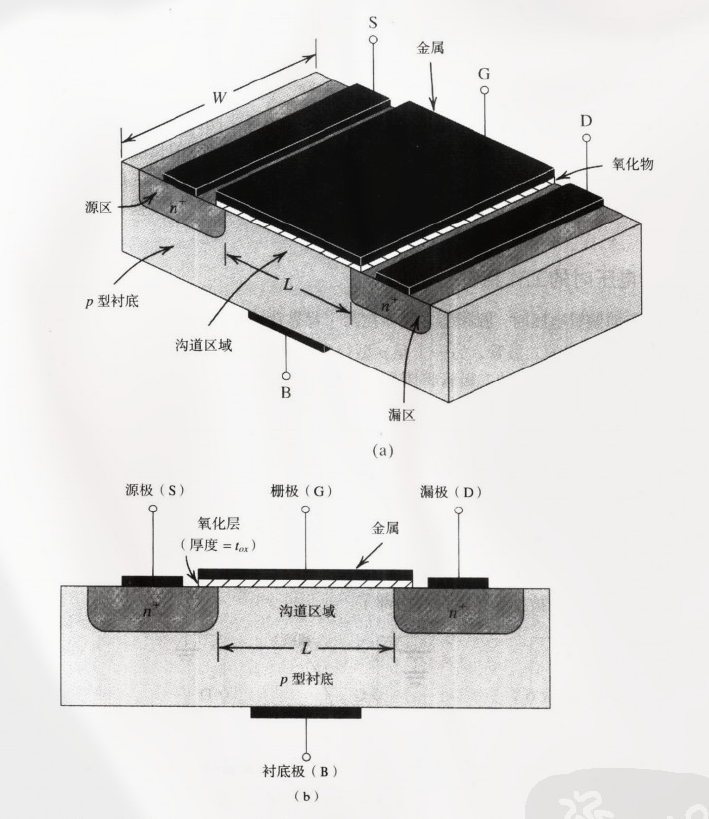
结构解释
最下面的结构为 p 型衬底 , 其本质是单晶硅原片. p 型 的含义是其是通过 p-type 掺杂形成的半导体 , 含有大量空穴 (positive)
其上有两个重掺杂的 n 型区, 即 $n^+$ 源区 和$n^+$ 漏区. n 型区 的以及就是 用 n-type 掺杂的半导体 组成. 源区 指电子流入, 漏区 指电子流出.
源区和漏区之间的区域用 一层二氧化硅绝缘层 覆盖.
最上面的黑色部分是 沉积在氧化层上的金属 从而形成的 栅极电极 .
由于其结构从上到下的组成为 金属-氧化物-半导体FET , 因此其被称为 MOSFET (Metal Oxide Semiconductor Field Effect Transistor)
端子解释
从图中可以看出, 在 4 处地方沉积了金属, 也就是说引出了 4 个电极, 即 4 个端子:
- 栅极 (G, Gate), 其用于控制导电带, 像一道门, 也就是 Gate
- 源极 (S, Source), 其相当于电流的来源, 是电子的源头, 也就是 Source
- 漏极 (D, Drain), 其相当于电子的去处, 也就是电子流走, 即 Drain
- 衬底极 (B, Body), 就是指最下层的衬底
注意, 氧化层的厚度 和 沟道区域 的宽度都是重要的参数.
MOSFET 的另一个名字叫 绝缘栅场效应管 (IGFET, Insulated-Gate Field-Effect Transistor) , 因为绝缘栅极的组成为绝缘体 (氧化层), 导致栅极的电流非常小 ( $10^{-15}$A )
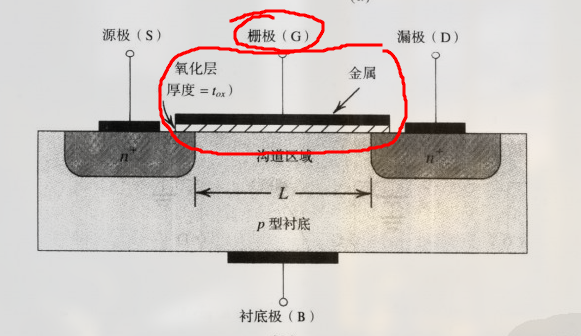
由于衬底为 p-type, 源区和漏区为 n-type, 这里会形成两个 pn 结.
在正常工作时, 这些 pn 结在任何时间都必须 反向偏置 , 由于漏区相对于源区有正电压, 因此将衬底电极连接到源极时, 可以使 pn 结截止 (不太明白)
由此, 可以认为衬底对器件的工作没有影响, 即将 MOSFET 视为一个 三端器件:
- 栅极 (G)
- 源极 (S)
- 漏极 (D)
4.1.2 无栅极电压时的工作特性
当栅极上没有加偏置电压时, 源和漏之间存在两个背靠背的串联二极管.
因此, 当加上电压 $V_{DS}$ 时, 这两个背靠背的二极管将阻碍从漏到源的电流的产生.
4.1.3 创建电流沟道
如图:
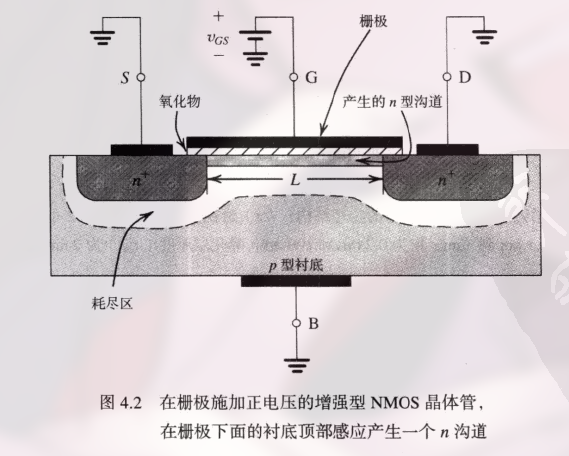
此时:
- 源极和漏极接地
- 栅极加上正电压
结果是, 栅极下衬底区域中的空穴被向下排斥, 自由电子被吸引到这个区域, 最终形成一个 n-type 区域, 此时源区和漏区被连接.
由于 n 型区域形成了从漏到源的电流流通的沟道, 这种 MOSFET 相应称为 n 沟道 MOSFET或称 NMOS 晶体管.
n 沟道是在 p 型衬底中形成的, 沟道的创建过程就是将衬底表面从 p 型转化成 n 型的过程, 因此感应产生的沟道也称为 反型层.
在沟道区域积聚足够数量的自由电子形成导电沟道时的 $V_{GS}$ 电压值称为开启电压, 记为 $V_t$
对于 n 沟道 FET , $V_t$ 为正.
MOSFET 的栅极和沟道之间形成了一个 平板电容器 , 氧化层作为该电容器的电介质.
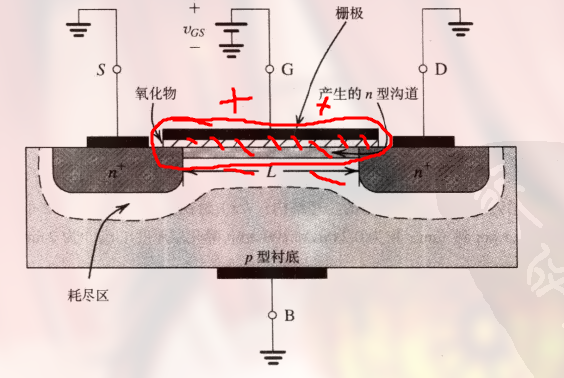
- 正电压使正电荷聚集在电容器上面的平板上 (栅极)
- 负电荷聚集在下面的板上
该电场 控制了沟道中的电荷量 (即确定了沟道的电导率)
4.1.4 施加一个小电压 $v_{DS}$
在产生沟道后, 在源和漏之间施加一个正电压 $V_{DS}$ (之前加上这个电压无法产生电流, 因为无法导通, 此时有沟道就能导通)
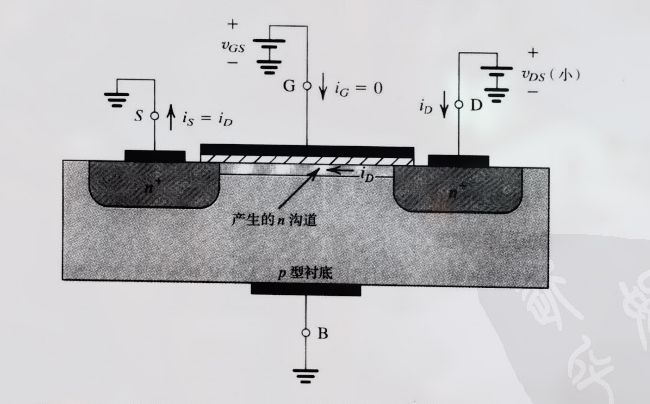
注意, 这里没有画出耗尽层区.
这里 从漏极到源极 的电流 $i_D$ 的大小和 $V_{GS} - V_t$ (被称为过栅电压, 有效电压, 或驱动电压, 因为 $V_t$ 时才产生沟道, 那个时候沟道中的电子密度低, 电流小) 成正比.
且电子密度 取决于 $V_{GS}$ 的大小.
理解
$V_{GS}$ 这个电压用于形成沟道, 如果不加 $V_{DS}$ 也不会形成电流.
对于 NMOS 晶体管, $V_{GS} > V_t$, 并且具有一个小的 $V_{DS}$ 电压, 则该器件相当于一个电阻, 其电阻值由 $V_{GS}$ 确定.
- $V_{GS} \le V_t$ 时, 电阻无穷大
- $V_{GS} > V_t$ 时, 电阻值随 $V_{GS}$ 增大而减小
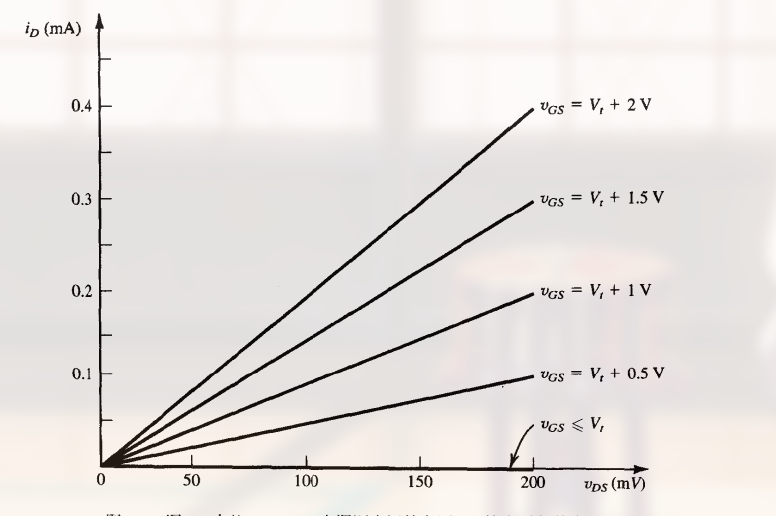
(可以看出, $V_{GS} - V_t$ 的值决定斜率的大小)
$$
\displaylines
{
i_D = (V_{GS} - V_t) V_{DS} \newline~ \newline
若 k = V_{GS} - V_t \newline~ \newline
i_D = k V_{DS} \newline~ \newline
可以看出是正比例函数
}
$$
由此可知, 在开启电压 $V_t$ 之上增大 $V_{GS}$ 将 增强沟道 , 即 增强模式工作和增强型 MOSFET 名字的由来.
注意:
- 流出源极的电流 $i_S$ 等于流入漏极的电流 $i_D$, 即 $i_S = i_D$
- 栅极电流 $i_G = 0$
例, 计算漏到源的电阻范围
$$
\displaylines
{
R = \frac{V_{DS}}{i_D} = V_{GS} - V_t
}
$$
可以看出电阻值由 $V_{GS} - V_t$ 决定.
4.1.5 $V_{DS}$ 增加时的工作特性
如图:
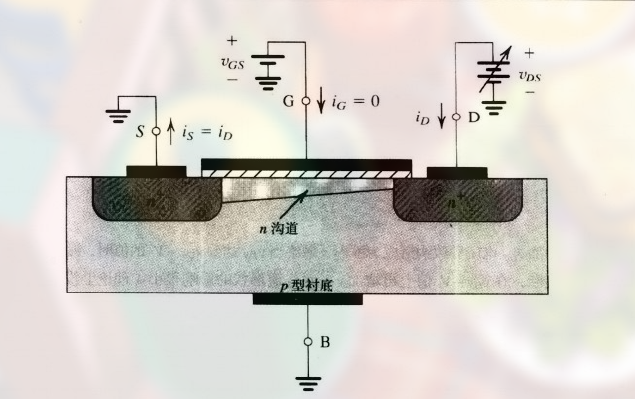
注意理解, $V_{DS}$ 相当于沟道长度两端的电压降, 因为漏区接电源, 电势为 $V_{DS}$; 源区接地, 电势为 $0$.
也可以说, 沿着沟道从源区到漏区, 电压从 0 增大到 $V_{DS}$.
已知了沟道两侧点的电势, 同时在栅极有电压 $V_{GS}$, 因此有:
- 源端电势为 $V_{GS} - 0 = V_{GS}$
- 漏端电势为 $V_{GS} - V_{DS}$
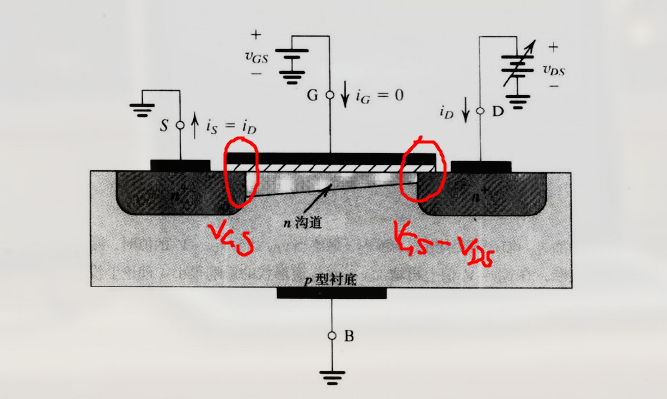
(中间 $V_{DS}$ 产生的电场不是匀强电场, 左端应该是 $V_{GS} - 0$, 右端是 $V_{GS} - V_{DS}$)
又由于 沟道深度取决于电压 , 因此 沟道深度不再均匀. 这里也就是锥形, 源端最深, 漏端最窄.
而当 $V_{DS}$ 增大时, 有:
$$
\displaylines
{
(V_{GS} - V_{DS}) \downarrow
}
$$
因此沟道会变得越来越尖, 同时阻值会相应增加, 导致 $i_D \sim V_{DS}$ 曲线不再是直线, 而是曲线.
当 $V_{DS}$ 增大到使栅极和漏端沟道之间的电压减小为 $V_t$ 时, 即 $V_{GS} - V_{DS} = V_t$ ( $V_t$ 为刚产生沟道的电压值 ), 此时 漏端的沟道深度减为 0 , 沟道被 夹断 .
此时的状态称为 饱和 , 继续增大 $V_{DS}$ 也不会影响沟道的形状, 流过沟道的电流也保持电压达到 $V_{DS} = V_{GS} - V_t$ 时 (也就是夹断的状态) 的值.
漏极电流达到饱和时, 也就是 MOSFET 进入饱和工作区 , 此时出现的电压 $V_{DS}$ 记为 $V_{DSsat}$
$i_D \sim v_{DS}$ 曲线如下:
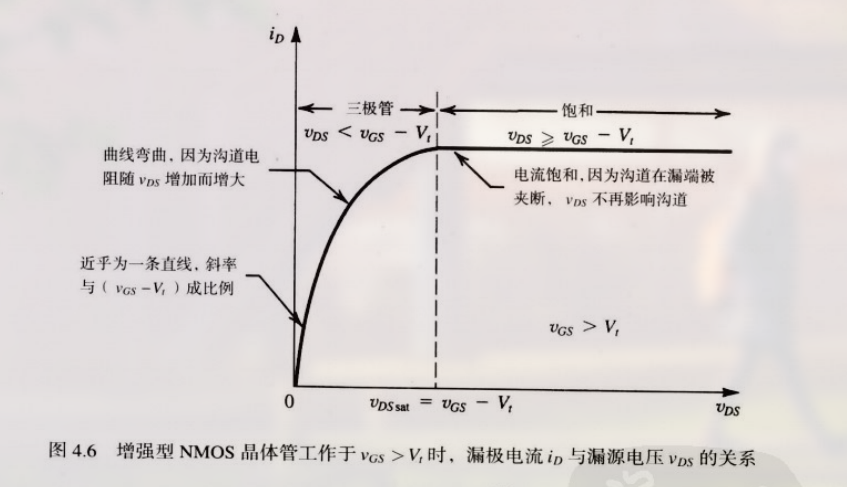
$V_{DSsat}$ 的值可以由下得到:
$$
\displaylines
{
V_{DSsat} = V_{GS} - V_t
}
$$
当:
- $V_{DS} \ge V_{DSsat}$ 时, 器件工作饱和区域在
- $V_{DS} < V_{DSsat}$ 时, 器件工作的区域称为三极管区 (或称为变阻区, 因为这段区域电阻阻值在改变)
4.1.6 $i_D \sim v_{DS}$ 关系的推导
这里, 先计算 $V_{DS}$ 产生的电场对一个无穷小沟道中的电荷的作用, 也就是产生的漂移电流, 然后再积分, 得到最终的漂移电流, 从而得到 $i_D \sim v_{DS}$ 的关系.
最终结果为:
$$
\displaylines
{
i_D = k V_{DS}( V_{OV} - \frac{1}{2}V_{DS} ) (变阻区) \newline~ \newline
i_D = \frac{1}{2} k V_{OV}^2 (饱和区)
}
$$
推导
如图:
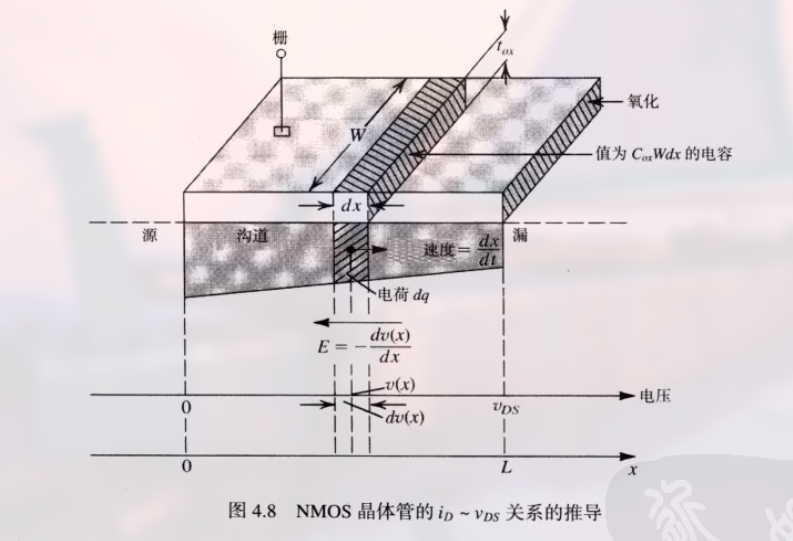
假设的条件为:
- $V_{GS} > V_t$, 以产生沟道
- $V_{DS} < V_{GS} - V_t$, 以工作在变阻区
同时, 单位栅极面积电容量记为 $C_{ox}$ (“ox” 应该就是 “oxygen” 的缩写), 氧化层的厚度为 $t_{ox}$ (其取决于 MOSFET 的工艺), 有:
$$
\displaylines
{
C = \epsilon_0 \frac{A}{d} \newline~ \newline
由于是单位面积, 就有 A = 1 \newline~ \newline
C_{ox} = \frac{\epsilon_{ox}}{t_{ox}}
}
$$
( $\epsilon_{ox}$ 是氧化硅的介电常数, 有 $\epsilon_{ox} = 3.9 \epsilon_0 = 3.9 \times 8.854 \times 10^{-12} = 3.45 \times 10^{-11} F/m$ )
考虑离源区距离为 $x$ 的无穷小的栅极条, 可以求得这个条的电容量:
$$
\displaylines
{
C = C_{ox} A \newline~ \newline
(C_{ox} 为单位面积的电容量) \newline~ \newline
C = C_{ox} W dx \newline~ \newline
(W 为宽度, W dx 指面积)
}
$$
求得电荷量所需的电压为栅极和沟道在 x 点之间的有效电压, 即 $V_{GS} - v(x) - V_t$, $v(x)$ 是沟道在 x 点处的电压, 因此可算出在 x 点的无穷小的沟道中含有的电子电荷 $dq$ 为:
$$
\displaylines
{
dq = -C_{ox} (W dx) [V_{GS} - v(x) - V_t] \newline~ \newline
( Q = CV )
}
$$
电压 $V_{DS}$ 沿负 x 方向产生的电场为:
$$
\displaylines
{
E(x) = - \frac{dv(x)}{dx} \newline~ \newline
( E = \frac{V}{d} )
}
$$
电场 $E(x)$ 使电子电荷 $dq$ 以速度 $dx/dt$ 漂向漏区:
$$
\displaylines
{
\frac{dx}{dt} = -\mu_n E(x) = \mu_n \frac{dv(x)}{dx} \newline~ \newline
(这里用的什么公式不太清楚)
}
$$
$\mu_n$ 是沟道中电子的迁移率 ( 即 表面迁移率, 其是一个物理参数, 具体值取决于工艺技术 )
因此可以得到漂移电流为:
$$
\displaylines
{
i = \frac{dq}{dt} \newline~ \newline
= \frac{dq}{dx} \frac{dx}{dt} \newline~ \newline
= - \mu_n C_{ox} W [V_{GS} - v(x) - V_t] \frac{dv(x)}{dx} \newline~ \newline
}
$$
可以得到 $i_D$ 为:
$$
\displaylines
{
i_D = -i = \mu_n C_{ox} W [V_{GS} - v(x) - V_t] \frac{dv(x)}{dx} \newline~ \newline
(为什么是相反数不太清楚) \newline~ \newline
i_D dx = \mu_n C_{ox} W [V_{GS} - v(x) - V_t] dv(x) \newline~ \newline
\int_0^L i_D dx = \int_0^{V_{DS}} \mu_n C_{ox} W [V_{GS} - v(x) - V_t] dv(x) \newline~ \newline
i_D = (\mu_n C_{ox}) ( \frac{W}{L} ) [(V_{GS} - V_{t})V_{DS} - \frac{1}{2} V^2_{DS}]
}
$$
( 此时为变阻区时的 $i_D \sim V_{DS}$ 特性的表达式 )
当处于饱和区时, 有 $V_{DS} = V_{GS} - V_t$, 即:
$$
\displaylines
{
i_D = \frac{1}{2}(\mu_n C_{ox})( \frac{W}{L} )( V_{GS} - V_t )^2
}
$$
由于 $\mu_n C_{ox}$ 是常数 (被称为工艺跨导参数, 其决定了 MOSFET 的跨导值), 因此记为 $k^\prime_{n}$, 量纲为 $A/V^2$:
$$
\displaylines
{
k^\prime_{n} = \mu_n C_{ox}
}
$$
因此最终有:
$$
\displaylines
{
i_D = k^\prime_{n} \frac{W}{L} [ (V_{GS} - V_t)V_{DS} - \frac{1}{2} V_{DS}^2 ] (变阻区) \newline~ \newline
i_D = \frac{1}{2} k^\prime_{n} \frac{W}{L} (V_{GS} - V_t)^2 (饱和区)
}
$$
若 $k = \frac{W}{L}\mu_n C_{ox}$, 以及 $V_{OV} = V_{GS} - V_t$ ( “OV” 指 “Override Voltage”, 过剩电压 ), 则式子可简化为:
$$
\displaylines
{
i_D = k V_{DS}( V_{OV} - \frac{1}{2}V_{DS} ) (变阻区) \newline~ \newline
i_D = \frac{1}{2} k V_{OV}^2
}
$$
可以看出, 漏极电流和沟道宽度与长度之比成正比, 沟道宽度与长度之比称为 MOSFET 的沟道宽长比
4.1.7 p 沟道 MOSFET
p 沟道增强型 MOSFET (PMOS 晶体管):
- 制造在 n 型衬底上
- 有 $p^+$ 型源区和漏区, 载流子是空穴
- $V_{GS}$ 和 $V_{DS}$ 的极性为负
- 开启电压 $V_t$ 为负
- 电流 $i_D$ 流入源极, 流出漏极
NMOS 器件可以做得更小, 运行更快, 并且 NMOS 比 PMOS 需要的电源电压更低.
4.1.8 互补 MOS 或 CMOS
CMOS 采用两种极性的 MOS 晶体管来制造, 且比 NMOS 更难制造.
CMOS 是所有 IC 技术中最广泛使用的技术, 既适用于模拟电路也适应于数字电路.
其 截面图 为:
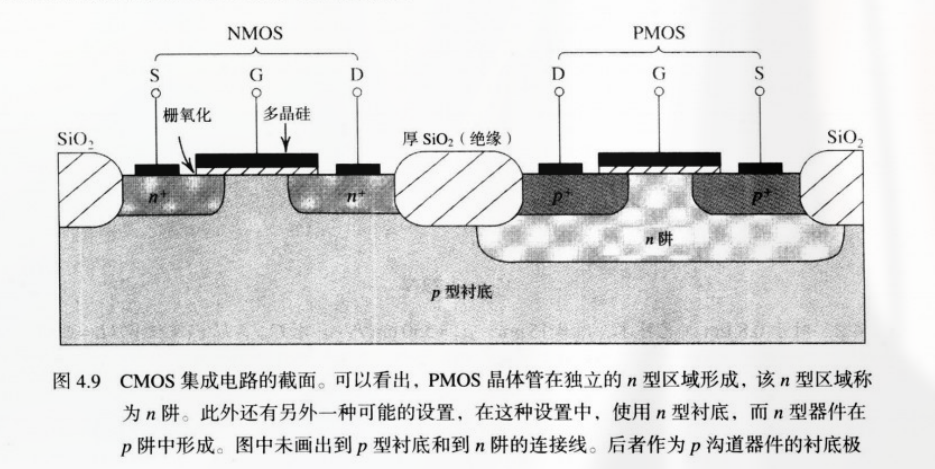
4.1.9 工作在亚阈区的 MOS 晶体管
对于 n 沟道 MOSFET 而言, 当: $V_{GS} < V_t$ 时, 没有电流流过, 器件截止. 但实际上, 在 $V_{GS}$ 的值小于但接近于 $V_t$ 时, 存在一个小的漏极电流, 这个区域称为 亚阈区 , 这里的漏极电流与 $V_{GS}$ 之间呈指数关系.
4.2 电流-电压特性
4.2.1 电路符号
最初的 n 沟道增强型 MOSFET 的电路符号为
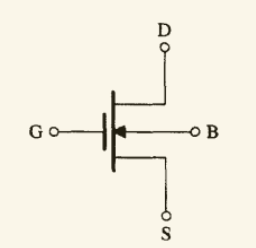
两条垂线之间的空间表明栅极和器件的衬底之间互相绝缘.
箭头 表明是 n 沟道器件. (n 沟道是 p 型衬底, 下面是正)
改进后的电路符号
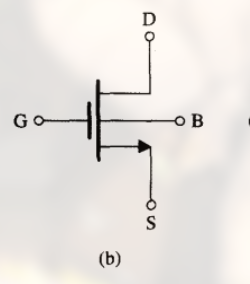
这里, 箭头 写在源极一侧, 箭头的方向 是电流的方向.
进一步简化的电路符号
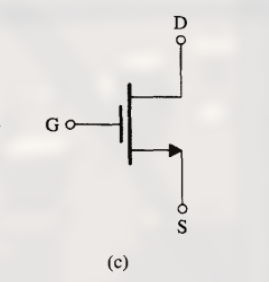
这种用于衬底对电路工作的影响不太重要的应用中.
4.2.2 $i_D \sim V_{DS}$ 特性
这里利用的电路为:
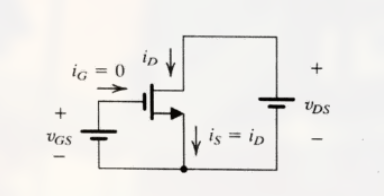
一组 $i_D \sim V_{DS}$ 的曲线, 每一条曲线都是在一个固定的 $V_{GS}$ 时测量得到的. (注意, 这里令 $k^\prime_n (W/L) = 1.0mA/V^2$ 以及 $V_t = 1V$)
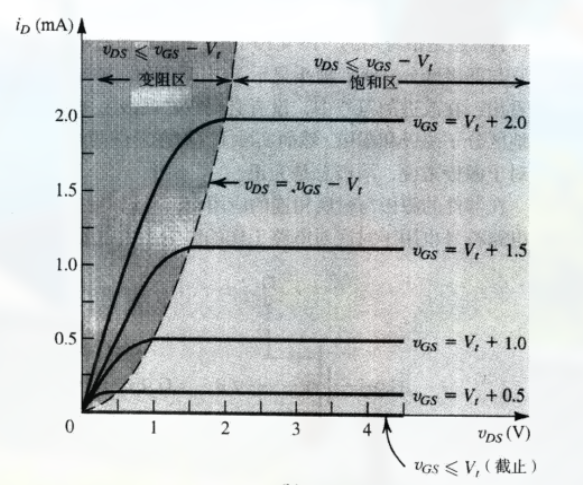
注意 这里的三个不同的工作区域: 截止区, 变阻区和饱和区:
- FET 用作放大器 , 利用饱和区
- FET 用作开关 , 利用截止区和变阻区
使 MOSFET 工作在变阻区的基本条件:
$$
\displaylines
{
V_{GS} \ge V_t \newline~ \newline
(产生沟道)
}
$$
使沟道保持连续, 是 工作在变阻区的另一个条件 , 确保栅极到漏极的电压满足:
$$
\displaylines
{
V_{OV} > V_{DS}
}
$$
在变阻区, $i_D \sim v_{DS}$ 特性的关系为:
$$
\displaylines
{
i_D = k^\prime_{n} \frac{W}{L} [ (v_{GS} - V_t)v_{DS} - \frac{1}{2} v_{DS}^2 ]
}
$$
如果 $v_{DS}$ 足够小, 则可以忽略 $v^2_{DS}$ 项. 因此原点附近 $i_D \sim v_{DS}$ 的特性关系为:
$$
\displaylines
{
i_D = k^\prime_{n} \frac{W}{L} (v_{GS} - V_t)v_{DS}
}
$$
此时的线性关系表明 MOS 晶体管作为一个线性电阻 工作, 其电阻值 $r_{DS}$ 由 $v_{GS}$ 控制:
$$
\displaylines
{
r_{DS} = \frac{v_{DS}}{i_D} \newline~ \newline
= [ k^\prime_{n} \frac{W}{L} (v_{GS} - V_t)v_{DS} ]^{-1} \newline~ \newline
(V_{DS} 小, v_{GS} = V_{GS})
}
$$
用 栅极到源极的过驱动电压 $V_{OV}$ 来表示 $r_{DS}$ 为:
$$
\displaylines
{
V_{OV} = V_{GS} - V_t \newline~ \newline
r_{DS} = 1/ [ k V_{OV} ]
}
$$
变阻区和饱和区的分界线 可以描述为:
$$
\displaylines
{
v_{DS} = V_{OV}
}
$$
有:
- $v_{GS} \ge V_t$ 时, 产生沟道
- $v_{DS} \le V_{OV}$ 时, 沟道连续
- $v_{DS} \ge V_{OV}$ 时, 沟道夹断
饱和电流 可以用分界线的 $v_{DS}$ 值求得:
$$
\displaylines
{
i_D = k^\prime_{n} \frac{W}{L} (v_{GS} - V_t)v_{DS} \newline~ \newline
v_{DS} = v_{GS} - V_t \newline~ \newline
i_D = \frac{1}{2} k^\prime_{n} \frac{W}{L} (v_{GS} - V_t)^2 \newline~ \newline
= \frac{1}{2} k V_{OV}^2
}
$$
可以看出, 在饱和时, MOSFET 提供的漏极电流与漏极电压 $v_{DS}$ 无关, 而由栅极电压 $v_{GS}$ 确定 .
(因为在饱和时, $v_{DS}$ 的增加不会影响沟道的形状, 这里不考虑 沟道长度调制效应)
此时的 MOSFET 可以视为一个 理想电流源
当栅极电压 $v_{GS}$ 变化时, 有:
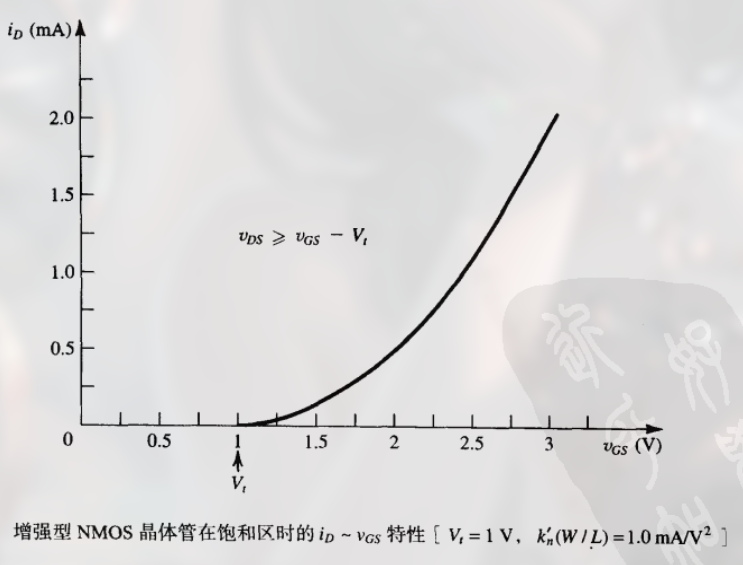
(注意, 这里同样是 $k^\prime_n (W/L) = 1.0mA/V^2$ 和 $V_t = 1V$ 时的特性)
增强型 NMOS 晶体管在饱和区的等效电路图为:
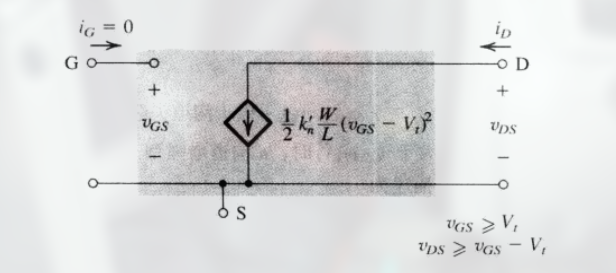
(左侧提供的是栅极电压, 右侧提供的是漏极电压, 下方是流出到源极, 中间是一个电流源)
4.2.3 饱和时的有限输出电阻
结论为
输出电阻不为无穷大:
$$
\displaylines
{
r_o = \frac{V_A}{I_D}
}
$$
推导
当考虑沟道长度调制效应时, $i_D$ 的饱和值与 $V_{DS}$ 相关.
沟道长度调制效应指: 漏极端的沟道被夹断时, 随着 $v_{DS}$ 的增加, 沟道夹断点会从漏端稍微移向源端, 因此长度从 $L$ 减小到 $L - \Delta L$.
其原因为: 加到漏极的多余电压呈现为漏区和沟道尾端之间的窄耗尽区两端的电压降, 该电压加速了沟道漏区一端的电子运动, 并将他们扫过耗尽区而进入漏区 (不是很明白这一段).
示意图为:
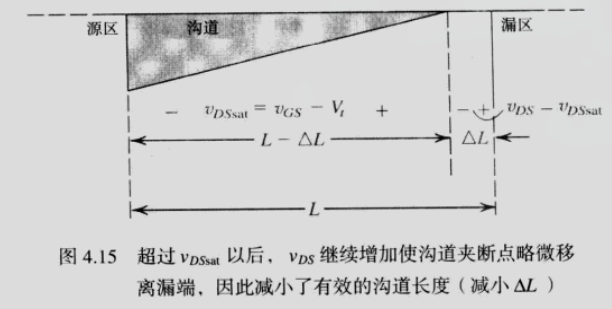
用 $L - \Delta L$ 替代 $i_D$ 和 $v_{DS}$ 的关系式中的 L 得:
$$
\displaylines
{
i_D = \frac{1}{2}k^\prime_{n} \frac{W}{L - \Delta L}(v_{GS} - V_t)^2 \newline~ \newline
= \frac{1}{2} k^\prime_{n}\frac{W}{L} \frac{1}{1- (\Delta L / L)} (v_{GS} - V_t)^2 \newline~ \newline
= \frac{1}{2} k^\prime_{n}\frac{W}{L} (1 + \frac{\Delta L}{L}) (v_{GS} - V_t)^2 \newline~ \newline
}
$$
若 $\Delta L$ 与 $v_{DS}$ 成正比, 则有:
$$
\displaylines
{
\Delta L = \lambda^\prime v_{DS} \newline~ \newline
i_D = \frac{1}{2} k^\prime_{n}\frac{W}{L} (1 + \frac{\lambda^\prime}{L}v_{DS}) (v_{GS} - V_t)^2 \newline~ \newline
(\lambda^\prime 是工艺参数, 量纲为 \mu m/V) \newline~ \newline
通常将 \lambda^\prime / L 记为 \lambda, 即: \newline~ \newline
\lambda = \frac{\lambda^\prime}{L} \newline~ \newline
最终有: \newline~ \newline
i_D = \frac{1}{2} k^\prime_{n}\frac{W}{L} (v_{GS} - V_t)^2 (1 + \lambda v_{DS})
}
$$
可以看出, $i_D$ 和 $v_{DS}$ 有线性关系. 因此观察 $i_D \sim v_{DS}$ 特性的反向延长线:
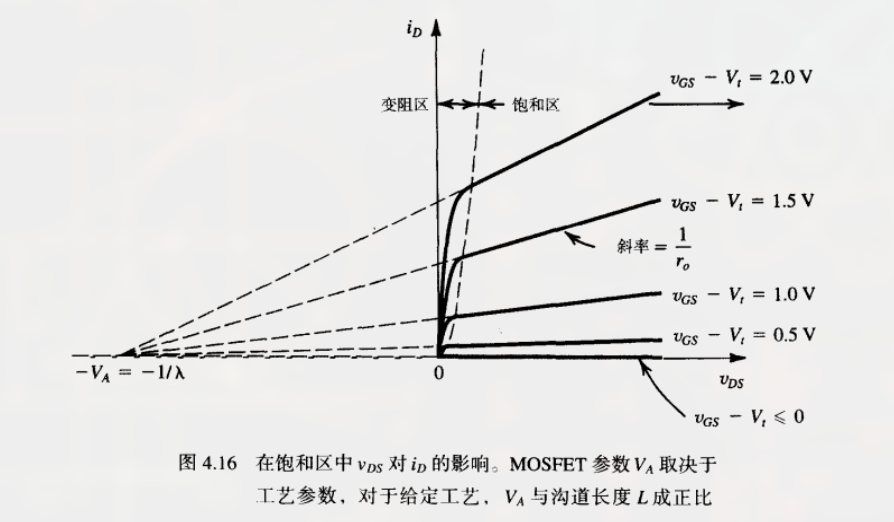
其与 $v_{DS}$ 轴相交于一点:
$$
\displaylines
{
i_D = \frac{1}{2}k^\prime_{n} \frac{W}{L} (v_{GS} - V_t)^2 (1 + \lambda v_{DS}) \newline~ \newline
当 v_{DS} = - \frac{1}{\lambda}, i_D = 0 \newline~ \newline
}
$$
因此这个点为 $(- \frac{1}{\lambda}, 0)$, 令:
$$
\displaylines
{
V_A = \frac{1}{\lambda}
}
$$
(可以看出 $V_A$ 也是一个工艺参数, 量纲为 V)
因此有这个点为 $(-V_A, 0)$, 而 $V_A$ 通常指厄尔利电压 (以 J.M. Early 名字命名).
$V_A$ 同时是最大的 $V_{DS}$ 的值, 也称为漏极反向击穿电压.
将 $L$ 从 $V_A$ 中分离出得:
$$
\displaylines
{
V_A = \frac{1}{\lambda} \newline~ \newline
= \frac{L}{\lambda^\prime}
}
$$
不考虑长度调制效应时, $i_D$ 的电流源的输出电阻为无穷大, 因为:
$$
\displaylines
{
r_o = [ \frac{\partial i_D}{\partial v_{DS}} ]^{-1} (v_{GS} 为常数) \newline~ \newline
v_{DS} 变化时, \partial i_D \approx 0 \newline~ \newline
r_o = \infty
}
$$
但此时, $v_{DS}$ 变化时, $i_D$ 也有了相应的变化, 因此此时的输出电阻不为无穷.
可以写为:
$$
\displaylines
{
r_o = [ \lambda \frac{k^\prime_n}{2} \frac{W}{L} (V_{GS} - V_t)^2 ]^{-1} \newline~ \newline
= \frac{1}{\lambda I_D} \newline~ \newline
= \frac{V_A}{I_D} \newline~ \newline
( I_D = \frac{k^\prime_n}{2} \frac{W}{L} (V_{GS} - V_t)^2, 是不考虑沟道长度调制效应时的漏极电流 )
}
$$
此时 NMOS 在饱和区的等效电路模型为:
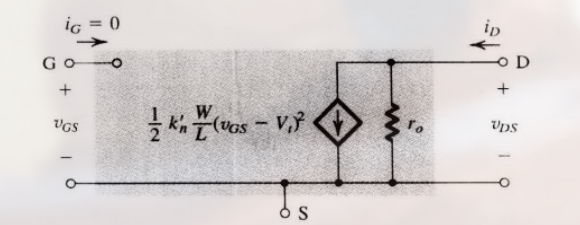
4.2.4 p 沟道 MOSFET 特性
- 为了使 PMOS 导通, 栅极电压必须至少比源极电压低 $\left\vert V_t \right\vert$
- 为了工作在变阻区, 漏极电压必须比栅极电压高 $\left\vert V_t \right\vert$
- 否则工作在饱和区
p 沟道增强型 MOSFET 的电路符号和改进后的电路符号以及简化符号为:
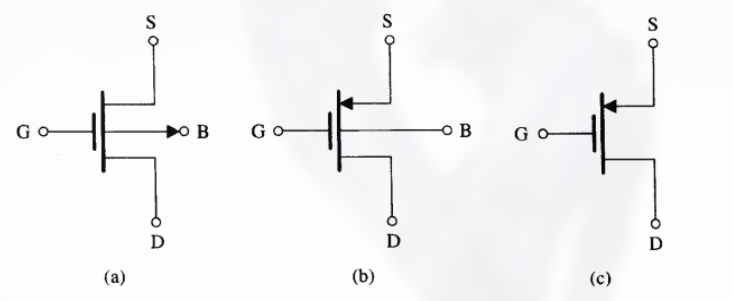
对于 p 沟道期间, 开启电压 $V_t < 0$, 因此, 为了形成沟道:
$$
\displaylines
{
v_{GS} \le V_t (形成沟道)
}
$$
栅极电压和漏极电压都添加负电压 , 电流从源极流向漏极.
工作在变阻区 需满足:
$$
\displaylines
{
v_{DS} \ge v_{GS} - V_t (连续沟道)
}
$$
$i_D \sim v_{DS}$ 的关系式为:
$$
\displaylines
{
i_D = k^\prime_p \frac{W}{L} [ (v_{GS} - V_t)v_{DS} - \frac{1}{2} v^2_{DS} ] \newline~ \newline
k^\prime_p = \mu_p C_{ox} \newline~ \newline
(\mu_p 是 p 沟道中的空穴的迁移率)
}
$$
工作在饱和区 , 需满足:
$$
\displaylines
{
v_{DS} \le v_{GS} - V_t (沟道夹断)
}
$$
$i_D \sim v_{DS}$ 的关系式为:
$$
\displaylines
{
i_D = k^\prime_p \frac{W}{L} (v_{GS} - V_t)^2 (1 + \lambda v_{DS})
}
$$
4.2.6 温度效应
$V_t$ 和 $k^\prime$ 都是温度敏感参数:
- 温度每增加 $1^\circ C$, $V_t$ 减小 2mV
4.3 MOSFET 直流电路
这里忽略沟道长度调制效应, 即假设 $\lambda = 0$.
- 对于 NMOS, $V_t$ 和 $V_{OV}$ 为正
- 对于 PMOS, $V_t$ 和 $V_{OV}$ 为负
($V_{OV} = V_{GS} - V_t$)
例题有用信息
$V_D > V_G$ 意味着 NMOS 工作在饱和区.
$$
\displaylines
{
V_{GS} - V_{DS} = V_G - V_S - ( V_D - V_S ) = V_G - V_D
}
$$
可以利用 $I_D$ 来求 $V_{GS}$
4.4 作为放大器和开关的 MOSFET
MOSFET 作为放大器应用的基础是: 它工作在饱和区域时相当于一个电压控制电流源. (栅极电压 $V_{GS}$ 的变化将导致漏极电流 $i_D$ 的变化)
饱和的 MOSFET 可以用来实现一个 互导放大器
(如何理解互导放大器, 就是指电压控制电流)
从基本的非线性器件中得到线性放大的技术:
- 利用直流偏置使 MOSFET 工作在一个合适的 $V_{GS}$ 和相应的 $I_D$ 上
- 在直流偏置电压 $V_{GS}$ 上叠加所要放大的电压信号 $v_{gs}$, 且将信号 $v_{gs}$ 保持在一个较小的范围内, 所得到的漏极电流的变化 $i_d$ 就与 $v_{gs}$ 成正比
4.4.1 大信号工作的传输特性
共源电路 (Common Source Circuit 或漏端接地电路) 如:
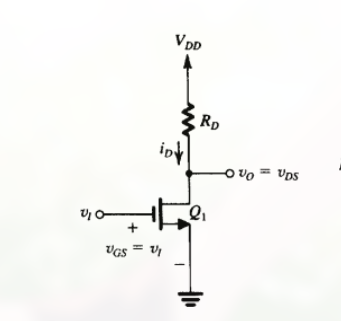
此电路为 二端口网络 (输入端 $v_i$ 和输出端 $v_o$ 两个端口)
名称由来: 接地的源极, 是, 栅极和源极组成的输入端, 以及, 漏极和源极组成的输出端, 的公共端.
该 MOSFET 放大器的输出电压为:
$$
\displaylines
{
v_O = v_{DS} = V_{DD} - R_D i_D
}
$$
4.4.2 传输特性的图解推导
共源放大器的性能受 MOSFET 的 $i_D \sim v_{DS}$ 特性及其关系的制约:
$$
\displaylines
{
v_{DS} = V_{DD} - R_D i_D \newline~ \newline
(这里v_{DS} = v_D, 因为Source端接地) \newline~ \newline
也就是可以写为: \newline~ \newline
v_{D} = V_{DD} - R_D i_D
}
$$
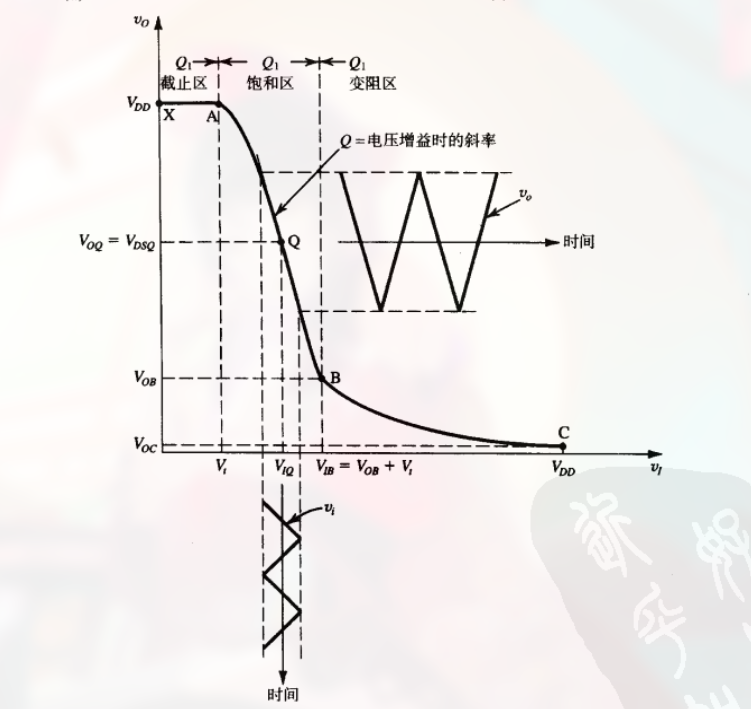
( $v_{DS}$ 就是指 $v_o$, $v_{GS}$ 指 $v_i$ )
这里是增大 $v_{GS}$ 导致电流 $I_D$ 增大, 进而导致 $v_{DS}$ 的变化.
或:
$$
\displaylines
{
i_D = \frac{V_{DD}}{R_{D}} - \frac{1}{R_D} v_{DS} \newline~ \newline
(同时除以 R_D)
}
$$
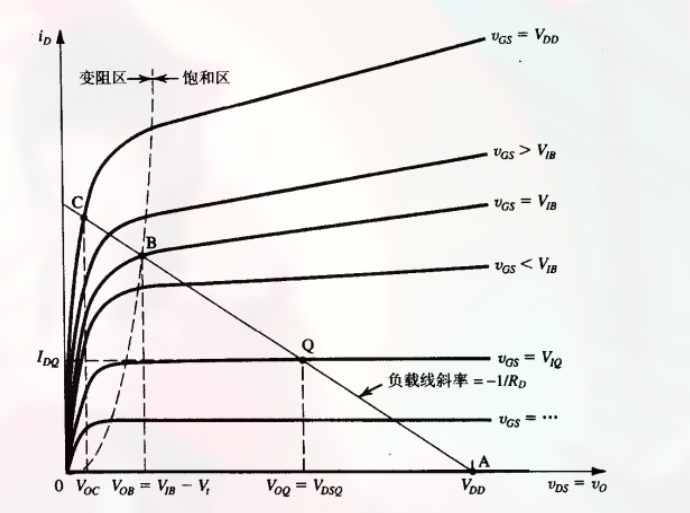
(此处的 $R_D$ 被认为是 放大器的负载电阻, 这里的直线称为 负载线 )
4.4.3 作为开关工作
$v_I$ 应该是指输入的直流信号, $v_i$ 指输入的交流信号.
如图:

通过使 $v_I < V_t$ ( $v_I$ 可能是 $V_{GS}$ ), 器件截止, 这样使得器件工作在线段 XA 中的某一点, 有 $v_O = V_{DD}$ (看图可以得到这个式子), 此时相当于 开关断开
当 $v_I$ 接近 $V_{DD}$ 时,开关导通 , 此时 $v_O$ 很小 (也就是这个器件分压小)
共源 MOS 电路可以用来作为 逻辑反相器 , 它的 “低” 电压接近 0 V (等效于逻辑0), “高” 电压接近 $V_{DD} (等效于逻辑1)$
4.4.4 作为线性放大器工作
为了使 MOSFET 作为放大器工作, 可使用传输曲线的饱和模式的一段, 同样是下图:

器件被偏置在接近曲线中间的点比较合适, 如 Q 点, 也被称为 直流偏置点或静态点 .
(这个点附近的特点为, $v_o$ 与 $v_i$ 具有相同的波形, 其相比输入增大了 $A_v$ 倍)
将所要放大的电压信号 $v_t$叠加在图中直流电压 $V_{IQ}$ 上, 当 $v_t$ 足够小时, 输出信号 $v_o$ 与 $v_t$ 就成线性关系 ( 小信号模型 ). 此时近似为 线性放大器 , $v_o$ 与 $v_i$ 具有相同的波形, 其相比输入增大了 $A_v$ 倍 ( $A_v$ 为放大器在 Q 点的电压增益 ):
$$
\displaylines
{
A_v = \frac{dv_o}{dv_I}(v_I = V_{I Q}) \newline~ \newline
(这里用 dv_o 和 dv_I 而不是 v_o 和 v_I 的原因可能是小信号)
}
$$
$\frac{dv_o}{dv_I}$ 同时也是传输曲线在偏置点 Q 处的斜率, 可以看出斜率为负, 因此基本 CS 放大器 (CS 指 Common Source) 为 反相放大器 .
注意 , 输入信号 $v_i$ 的幅度增大, 输出信号会发生失真, 因为其不再被限制在线性部分.
(如果太大二次方的那部分就不能被忽略)
对于偏置点 Q 的位置的选取 , 需满足 $V_{DSQ}$ 远小于 $V_{DD}$ 且远大于 $V_{OB}$
(也就是位于饱和区)
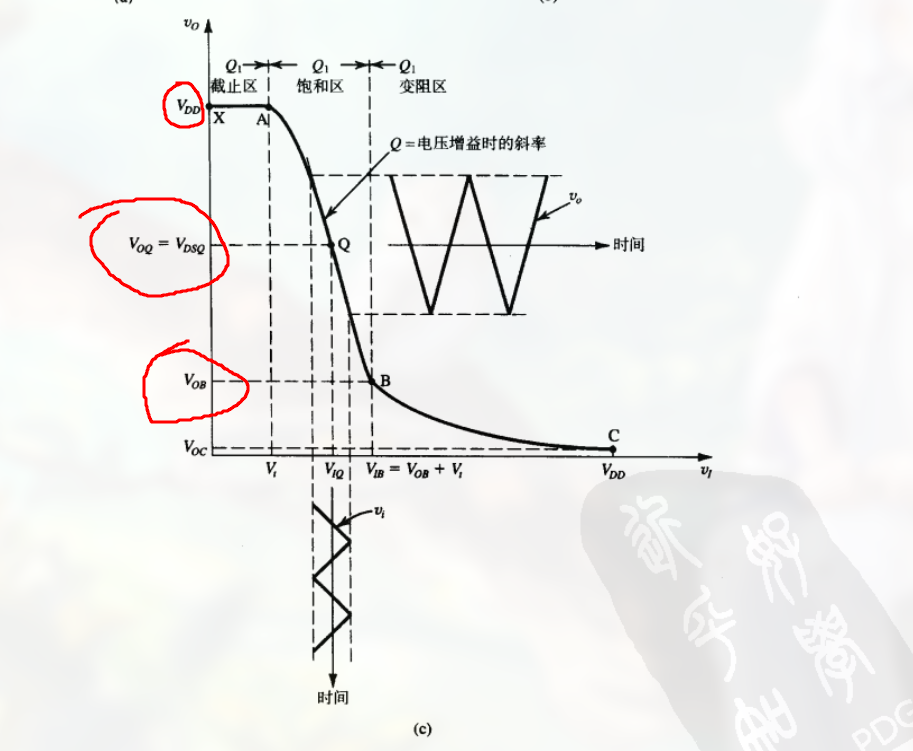
注意一个名词 – 摆幅空间
- 当 $V_{DSQ}$ 接近于 $V_{DD}$ 时, 由于此时 MOSFET 被截止, 输出信号正波峰可能被限制在 $V_{DD}$ 而引起顶部限幅, 此时称为 没有足够的 “正摆幅空间”
- 当 $V_{DSQ}$ 接近变阻区的分界线时, 在负波峰附近的时间里 MOSFET 将进入变阻区, 导致信号失真, 此时称为 没有足够的 “负摆幅空间”
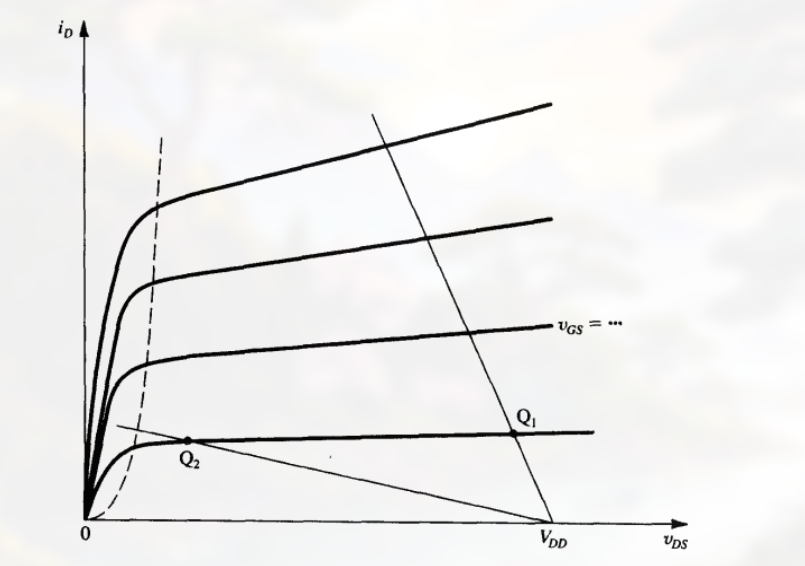
此处为, 两条负载线和相应偏置点:
- 偏置点 $Q_1$ 没有为漏极电压正摆幅流出足够的空间
- 偏置点 $Q_2$ 太接近变阻区的分界线而不能输出足够的负信号摆幅
4.4.5 传输特性的解析表达式
以下 CS 的三段传输特性的解析表达式, 可以用 MOSFET 在三个区域 (截止区, 饱和区和变阻区) 的伏安特性关系推导出:

同样需要看这个图:

截止区域段, XA (上图的线段)
有:
$$
\displaylines
{
v_I \le V_t, v_O = V_{DO}
}
$$
饱和区域段, AQB
有:
$$
\displaylines
{
v_I \ge V_t, v_O \ge v_t - V_t
}
$$
忽略沟道长度调制效应时, 将:
$$
\displaylines
{
i_D = \frac{1}{2} (\mu_n C_{ox}) ( \frac{W}{L} ) ( v_I - V_t )^2
}
$$
带入 $v_o = V_{DD} - R_D i_D$, 得:
$$
\displaylines
{
v_O = V_{DD} - \frac{1}{2}R_D \mu_n C_{ox} \frac{W}{L} (v_I - V_t)^2
}
$$
可由此得到增量电压增益 $A_v$ 的表达式:
$$
\displaylines
{
A_v = \frac{dv_O}{dv_I}(v_I = V_{IQ}) \newline~ \newline
= -R_D \mu_n C_{OX} \frac{W}{L} (V_{IQ} - V_t) \newline~ \newline
( 也就是求导 )
}
$$
(从这里可以看出和 $A_v$ 成正比的量)
推导一个简单有用的电压增益表达式:
将 $v_I = V_{IQ}$, $v_O = V_{OQ}$ 和 $V_{OV} = V_{IQ} - V_t$ 代入
$$
\displaylines
{
v_O = V_{DD} - \frac{1}{2}R_D \mu_n C_{ox} \frac{W}{L} (v_I - V_t)^2
}
$$
得:
$$
\displaylines
{
V_{OQ} = V_{DD} - \frac{1}{2}R_D \mu_n C_{ox} \frac{W}{L} V_{OV}^2 \newline~ \newline
-R_D \mu_n C_{OX} \frac{W}{L} V_{OV} = 2 \frac{V_{OQ} - V_{DD}}{V_{OV}}
}
$$
代回:
$$
\displaylines
{
A_v = -R_D \mu_n C_{OX} \frac{W}{L} (V_{IQ} - V_t) \newline~ \newline
}
$$
得:
$$
\displaylines
{
A_v = - \frac{2(V_{DD} - V_{OQ})}{V_{OV}} \newline~ \newline
= - \frac{2V_{RD}}{V_{OV}}
}
$$
( $V_{RD}$ 是漏极电阻 $R_D$ 两端的直流电压, 即 $V_{RD} = V_{DD} - V_{OQ}$ )
变阻区域段, BC
有:
$$
\displaylines
{
v_I \ge V_t \newline~ \newline
v_O \le v_I - V_t
}
$$
将 $i_D$:
$$
\displaylines
{
i_D = \mu_n C_{OX} \frac{W}{L} [ (v_I - V_t)v_O - \frac{1}{2}v_O^2 ]
}
$$
带入:
$$
\displaylines
{
v_O = V_{DD} - R_D i_D
}
$$
得:
$$
\displaylines
{
v_O = V_{DD} - R_D \mu_n C_{OX} \frac{W}{L} [ (v_I - V_t)v_O - \frac{1}{2}v_O^2 ]
}
$$
当 $v_O$ 较小时的一段曲线可近似为:
$$
\displaylines
{
v_O \sim V_{DD} - R_D \mu_n C_{OX} \frac{W}{L} (v_I - V_t)v_O \newline~ \newline
= \frac{V_{DD}}{[ 1 + R_D \mu_n C_{OX} \frac{W}{L} (v_I - V_t) ]}
}
$$
该式结合 $i_D - v_{DS}$ 平面的原点附近漏极到源极的电阻 $r_{DS}$ 的表达式:
$$
\displaylines
{
r_{DS} = \frac{1}{\mu_n C_{OX} \frac{W}{L} (v_I - V_t)}
}
$$
得:
$$
\displaylines
{
v_O = V_{DD} \frac{r_{DS}}{r_{DS} + R_D}
}
$$
(一个分压表达式)
从这个式子可以看出, 当 $v_O$ 较小时, MOSFET 相当于一个电阻 $r_{DS}$(其值由 $v_I$ 决定), 该电阻与 $R_D$ 一起组成对 $V_DD$ 进行分压的一个电压分压器.
通常 $r_{DS} \ll R_D$ , 因此上式可简化为;
$$
\displaylines
{
v_O = V_{DD} \frac{r_{DS}}{R_D}
}
$$
4.5 MOS 放大电路的偏置
4.5.1 采用固定 $V_{GS}$ 的偏置
对 MOSFET 进行偏置最直接的方法是将它的栅源电压 $V_{GS}$ 固定, 且能够提供所需要的 $I_D$ 值.
但这 不是 MOSFET 偏置的好方法 .
原因
因为:
$$
\displaylines
{
I_D = \frac{1}{2} \mu_n C_{OX} \frac{W}{L} (V_{GS} - V_t)^2
}
$$
当 $V_{GS}$ 固定时, $I_D$ 的值就与生产工艺以及温度相关密切, 导致不同器件在同一 $V_{GS}$ 下的漏极电流值的差别很大:
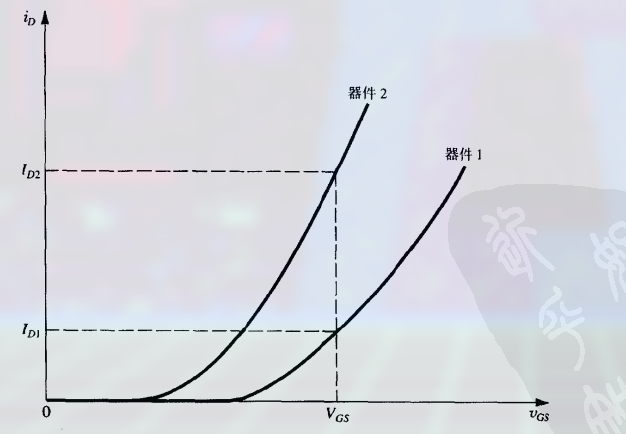
4.5.2 源极接电阻的固定 $V_G$ 偏置
固定栅极上的直流电压 $V_G$ 并在源极连接上一个电阻:
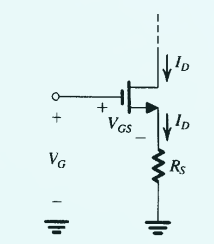
有:
$$
\displaylines
{
V_G = V_{GS} + R_S I_D
}
$$
此时:
- 如果 $V_G$ 远大于 $V_{GS}$, $I_D$ 将主要由 $V_G$ 和 $R_S$ 的值确定
- 即使 $V_G$ 不是远大于 $V_{GS}$, 电阻 $R_S$ 可以提供负反馈, 稳定偏置电流 $I_D$ 的值
稳定电流
当 $I_D$ 由于某种原因增大时, 由于 $V_{G}$ 不变, 因此 $V_{GS}$ 减小.
由于:
$$
\displaylines
{
I_D=\frac{1}{2} \mu_n C_{OX} \frac{W}{L} (V_{GS} - V_t)^2
}
$$
$V_{GS}$ 的减小又会导致 $I_D$ 减小 (意料之外的变化为变大, 这里又使其变小, 与原变化相反, 起到负反馈作用)
$R_S$ 的作用就是保持漏极电流 $I_D$ 尽可能稳定, 因此其称 衰减电阻
两种可能的实际实现电路:
- 第一种
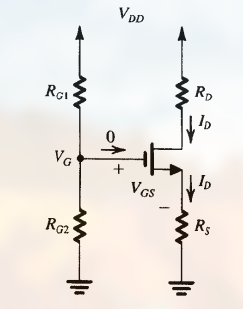
其使用 单电源 $V_{DD}$ 并通过 电压分压器 ( $R_{G1}, R_{G2}$ ) 得到 $V_G$
不是很明白的部分 :

- 第二种
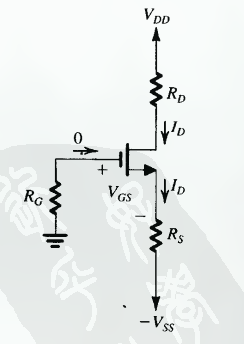
采用 两个电源 , 用 $V_{SS}$ 代替 $V_G$.
4.5.3 栅源间接反馈电阻的偏置
使用连接在漏极和栅极之间的反馈电阻进行偏置:
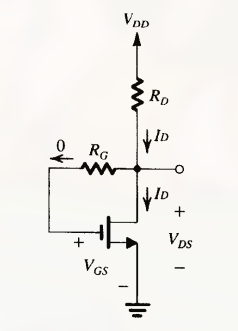
反馈电阻 $R_G$ 为大电阻 ( $M\Omega$ 数量级 ), 其使 栅极直流电压等于漏极直流电压 ( 因为 $I_G = 0$ )
因此有:
$$
\displaylines
{
V_{GS} = V_{DS} = V_{DD} - R_D I_D \newline~ \newline
V_{DD} = V_{GS} + R_D I_D
}
$$
使用耦合电容来加上信号不会破坏已经建立的直流偏置条件.
4.5.4 恒流源偏置
对 MOSFET 放大器进行偏置的最有效的方法是 使用恒流源 .
恒流源两端有一个压降.
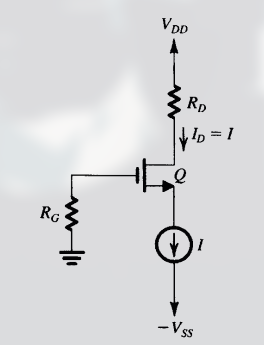
其中, $R_G$ 是大电阻 ( $M\Omega$ 数量级 ), $R_D$ 用于在漏极上建立合适的直流电压, 确保晶体管工作在饱和区.
I 是恒流源. 其实现电路为:
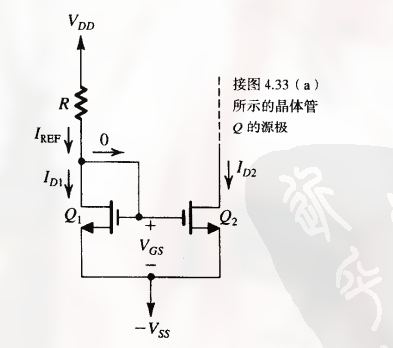
其包含两个晶体管 $Q_1, Q_2$.
对于 $Q_1$, 其漏极与栅极短路, 因此工作在饱和区 (不是很明白), 有:
$$
\displaylines
{
I_{D1} = \frac{1}{2} k V_{OV}^2
}
$$
(这里忽略了沟道长度调制效应)
$Q_1$ 的漏极电流由 $V_{DD}$ 通过 R 提供, 且栅极电流为 0, 因此有:
$$
\displaylines
{
I_{D1} = I_{REF} = \frac{V_{DD} + V_{SS} - V_{GS}}{R}
}
$$
$I_{REF}$ 指流过 R 的电流, 被称为 电流源的参考电流
对于 $Q_2$ , 其与 $Q_1$ 有相同的 $V_{GS}$, 如果其工作在饱和区, 则其漏极电流为;
$$
\displaylines
{
I = I_{D2} = \frac{1}{2} k V_{OV}^2
}
$$
(也忽略了沟道调制效应)
最终得到电流为:
$$
\displaylines
{
I = I_{REF} \frac{(W/L)_2}{(W/L)_1}
}
$$
(不知道怎么得到的)
该电路也被称为 镜像电流源 .
4.6 小信号工作与小信号模型
可以通过对 MOSFET 进行偏置使其工作在饱和区并保持输入信号足够小以实现线性放大.
通过下图来分析小信号放大器性能:
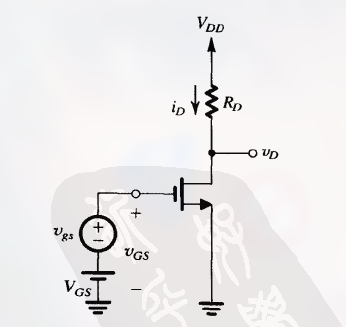
这里用直流电压 $V_{GS}$ 进行偏置, 所要放大的输入信号 $v_{gs}$ 被叠加在直流偏置电压上, 输出电压 从漏极获得.
4.6.1 直流偏置点
当信号 $v_{gs} = 0$ 时, 直流偏置电流 $I_D$ 为:
$$
\displaylines
{
I_D = \frac{1}{2} k V_{OV}^2
}
$$
(这里忽略了沟道长度调制效应, 即假定 $\lambda=0$)
直流偏置点指的可能就是所加的 直流电压值
漏极直流电压 $V_{DS}$ 为:
$$
\displaylines
{
V_{DS} = V_{DD} - R_D I_D
}
$$
确保工作在饱和区, 必须有:
$$
\displaylines
{
V_{DS} > V_{GS} - V_t
}
$$
4.6.2 漏极信号电流
当加上 $v_{gs}$ 后, 栅源电压的总瞬时量为:
$$
\displaylines
{
v_{GS} = V_{GS} + v_{gs}
}
$$

此时得到的总瞬时漏极电流 $i_D$ 为:
$$
\displaylines
{
i_D = \frac{1}{2} k (V_{GS} + v_{gs} - V_t)^2 \newline~ \newline
= \frac{1}{2} k (V_{GS} - V_t)^2 + k (V_{GS} - V_t)v_{gs} + \frac{1}{2} k v_{gs}^2
}
$$
可以看出, 第三项是非线性的, 其表示了非线性失真, 而当输入信号足够小 时, 使得:
$$
\displaylines
{
\frac{1}{2} k v_{gs}^2 \ll k (V_{GS} - V_t)v_{gs} \newline~ \newline
v_{gs} \ll 2(V_{GS} - V_t) \newline~ \newline
v_{gs} \ll 2V_{OV}
}
$$
(即第二项远大于第三项)
此时可以忽略最后一项, 有:
$$
\displaylines
{
i_D = I_D + i_d \newline~ \newline
其中: \newline~ \newline
i_d =k (V_GS - V_t) v_{gs}
}
$$
可以用 跨导 $g_m$ 将 $i_d$ 和 $v_{gs}$ 关联起来:
$$
\displaylines
{
g_m = \frac{i_d}{v_{gs}} = k (V_{GS} - V_t) \newline~ \newline
= k V_{OV}
}
$$
示意图:
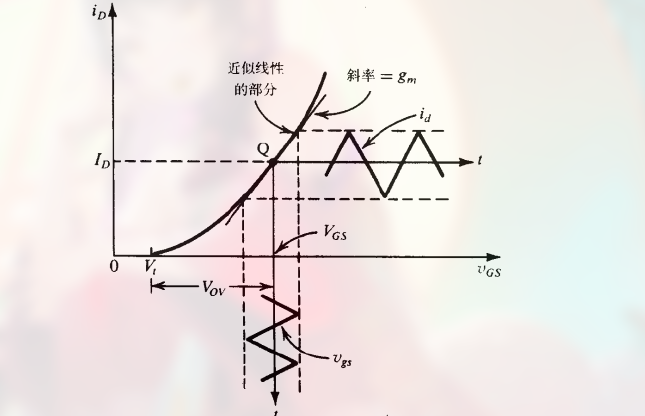
对于 “跨导” 中的 “跨” 的理解
用电压控制电流, 相当于从电压 “跨” 到了电流.
4.6.3 电压增益

用 $v_D$ 表示总的瞬时漏极电压, 有:
$$
\displaylines
{
v_D = V_{DD} - R_D i_D
}
$$
在小信号条件下:
$$
\displaylines
{
v_D = V_{DD} - R_D (I_D + i_d) \newline~ \newline
= V_D - R_D i_d \newline~ \newline
(这里的转换不清楚)
}
$$
因此漏极电压的信号分量为:
$$
\displaylines
{
v_d = -i_d R_D = -g_m v_{gs} R_D
}
$$
(问题, 不同符号的含义)
电压增益为:
$$
\displaylines
{
A_v = \frac{v_d}{v_{gs}} = -g_m R_D
}
$$
这里的负号 表明输出信号 $v_d$ 与输入信号 $v_{gs}$ 有 $180^\circ$ 的相位差. (毕竟是正弦信号)
如: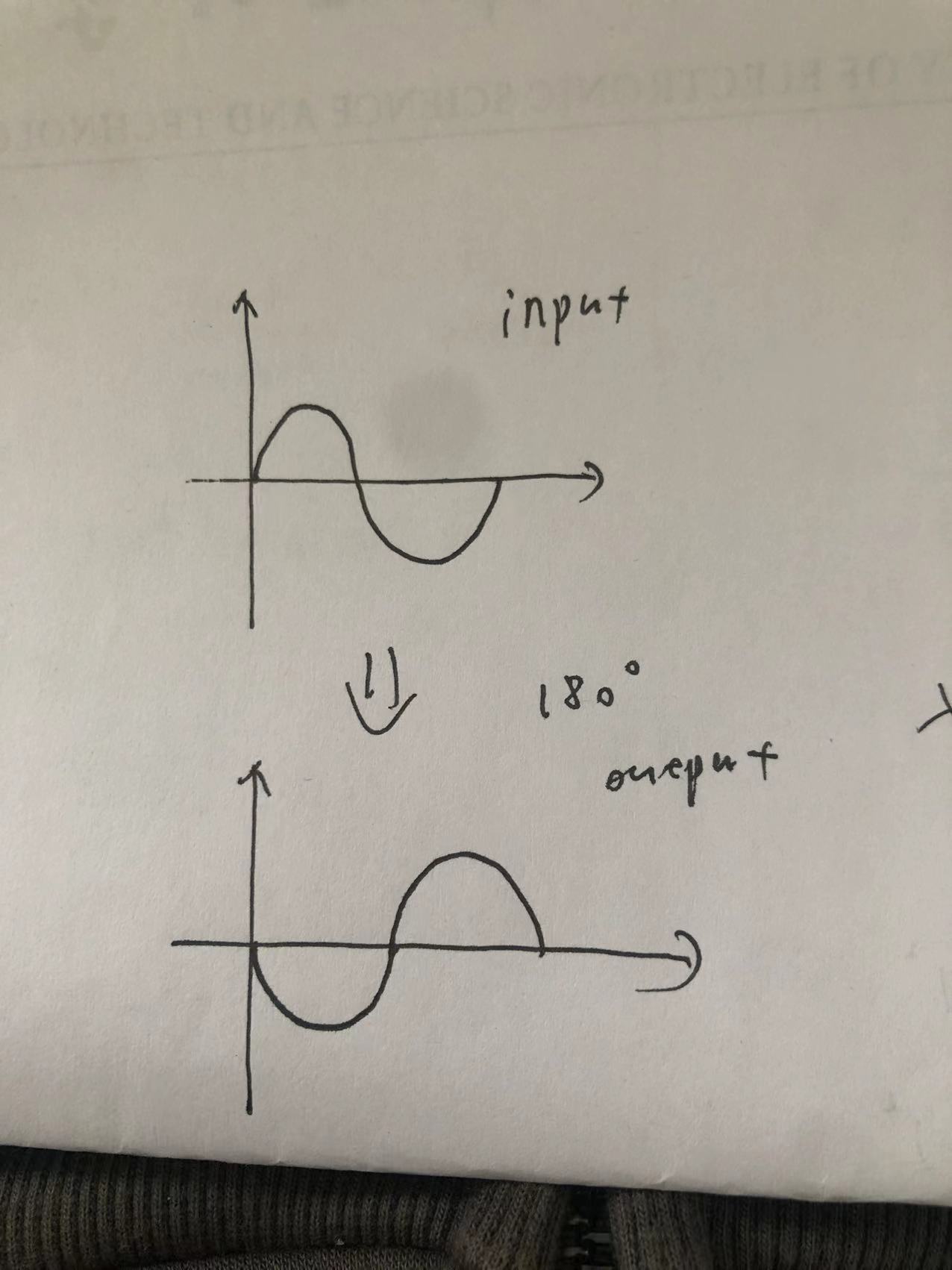
注意这里都是 电压放大器.
4.6.4 直流分析和信号分析的分离
将直流计算和小信号分开可以大大简化分析和设计.
一旦建立了稳定的直流工作点并通过计算得到所有直流量, 就可以忽略直流量来进行信号分析.
(不知道为什么)
4.6.5 小信号等效电路模型
从信号的观点看, FET 相当于一个电压控制电流源:
- 在栅极和源极之间输入信号 $v_{gs}$, 在漏极输出电流 $g_m v_{gs}$
- 输入电阻非常高, 理想情况为无穷大
- 输出电阻也很高, 目前假设为无穷大
以上同时为 MOSFET 的小信号特性, 其等效电路为:
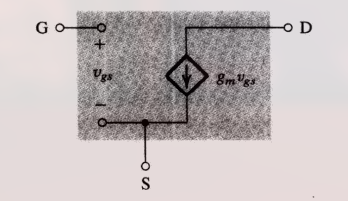
注意这里的 理想直流恒流源开路 , 因为直流恒流源的信号电流总为 0 (电阻为无穷大).
该模型的缺陷在于 其假定饱和区的漏极电流与漏极电压无关, 但实际上其受 $v_{DS}$ 的线性影响, 这种影响可以用 漏极和源极之间的一个有限电阻 $r_O$ 来建模.
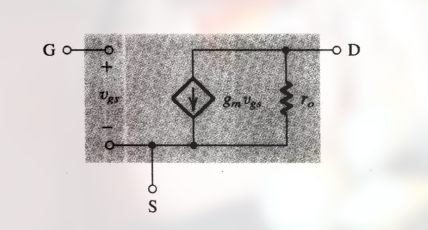
这里并联的原因为: 原本的总电流只有电流源一条支路, 增加一条支路后, 电流增加 $\frac{v_{DS}}{r_O}$, 或者说, 电流源的内阻就是和电流源并联表示.
$$
\displaylines
{
r_O = \frac{ \left\vert V_A \right\vert }{I_D}
}
$$
( $V_A = \frac{1}{\lambda}$, 其与 MOSFET 的沟道长度成正比 $I_D$ 是不考虑沟道长度调制效应时的漏极直流电流值 $I_D = \frac{1}{2} k V_{OV}^2$ )
此时电压增益表达式为:
$$
\displaylines
{
A_v = \frac{v_d}{v_{gs}} = -g_m (R_D // r_O)
}
$$
注意, 小信号模型参数 $g_m$ 和 $r_O$ 与 MOSFET 的直流偏置点有关 (因为 $g_m = k V_{OV} = k( V_{GS} - V_t )$).
4.6.6 跨导 $g_m$
MOSFET 的跨导:
$$
\displaylines
{
g_m = \frac{i_d}{v_{gs}} = k (V_{GS} - V_t) \newline~ \newline
= k V_{OV}
}
$$
可以看出, $g_m$ 与:
- 工艺互导参数 $k_n^\prime = \mu_n C_{OV}$
- $\frac{W}{L}$
- 驱动电压 $V_{OV} = V_{GS} - V_t$
成正比.
若要得到较大的跨导, 该器件 沟道必须短而宽
通过对器件偏置更大的 $V_{GS}$ 来增加 $g_m$有一个缺点 , 其会减小漏极短允许的电压信号幅度 (为什么).
将上式中的 $V_{OV}$ 用 $\sqrt{2 I_D / (k_n^\prime (W / L))}$ 替换, 可以得到一个有用的表达式:
$$
\displaylines
{
g_m = \sqrt{2k_n^\prime} \sqrt{W / L} \sqrt{I_D}
}
$$
其表明:
- 对于给定的 MOSFET, $g_m$ 与直流偏置电流的平方根成正比
- 对于 给定的偏置电流 , $g_m$ 与 $\sqrt{W/L}$ 成正比
(其跨导与器件的形状有关)
双极型晶体管 (BJT) 的跨导与偏置电流成正比, 而与器件的物理尺寸和几何形状无关.
将下式中:
$$
\displaylines
{
g_m = \frac{i_d}{v_{gs}} = k (V_{GS} - V_t) \newline~ \newline
= k V_{OV}
}
$$
的 $k$ 用 $2I_D / (V_{GS} - V_t)^2$ 代替, 得:
$$
\displaylines
{
g_m = \frac{2I_D}{V_{GS} - V_t} = \frac{2I_D}{V_{OV}}
}
$$
因此, 可以用三个不同的关系式确定 $g_m$.
4.6.7 T 等效模型
T 等效模型的变换过程如下:
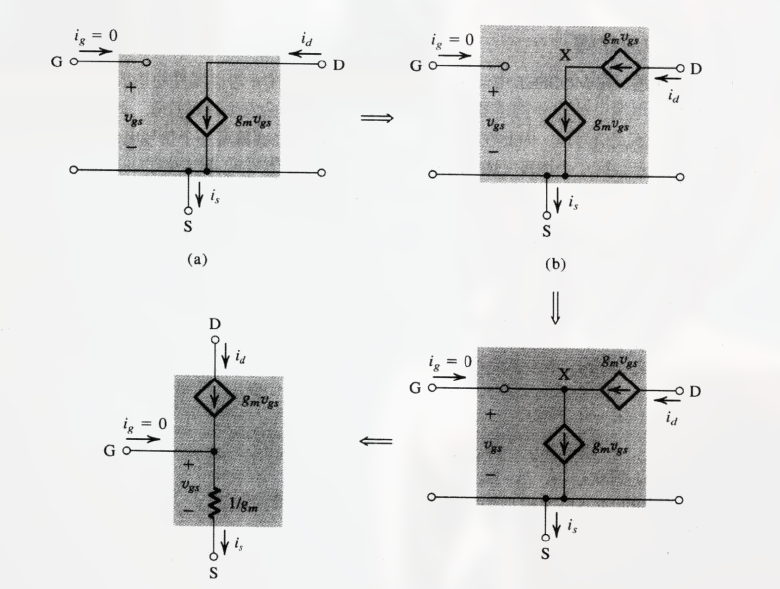
(这里先不考虑 $r_O$)
第一步
增加一个 $g_m v_{gs}$ 电流源与原来的受控源串联.
此时, 端口电流( $i_d 和 i_s$ )没有变化 (两个电流源两端的电流大小相等, 都是 $g_m vv_{gs}$)
第二步
创建新的标为 X 的电路节点与栅极 G 合在一起.
此时, 栅极电流没有变化, 仍然为 0.
(中间的空心点可能表示断路)
第三步
用一个电阻, 替换连接在控制电压 $v_{gs}$ 两端的受控源. 只要 该电阻与受控源有相同的电流 即可. (源吸收定理?)
该电阻值为 $v_{gs} / g_m v_{gs} = 1 / g_m$
变换之后的各参数没有变化:
- $i_g = 0$
- $i_d = g_m v_{gs}$
- $i_s = v_{gs} / (1/g_m) = g_m v_{gs}$
- 栅源之间的电阻为无穷大
若考虑 $r_O$ 则在漏极和源极之间接入电阻 $r_O$ ($r_O$ 是什么)
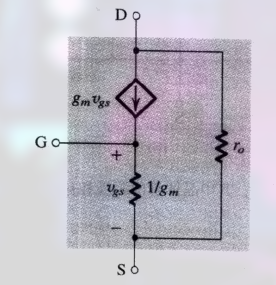
为了区分, 下图又被称为 混合 $\pi$ 模型

T 模型和 Pi 模型各自的优势
- 如果MOSFET源极连接了确定的电势点(如地GND),用Pi模型将较好分析
- 如果MOSFET源极额外的接了一个电阻,或其他器件,用T模型替代MOS将更便于分析
4.6.8 衬底效应建模
暂时跳过
4.7 单极 MOS 放大器
因为在分离电路中 MOSFET 源极通常连接到衬底极, 因此衬底效应可以忽略.
在某些电路中, 为了使分析简单也忽略 $r_O$, 而把注意力集中在放大器组态的主要特征上.
4.7.1 基本结构
实现分立电路 MOS 放大器不同组态的基本电路如下:
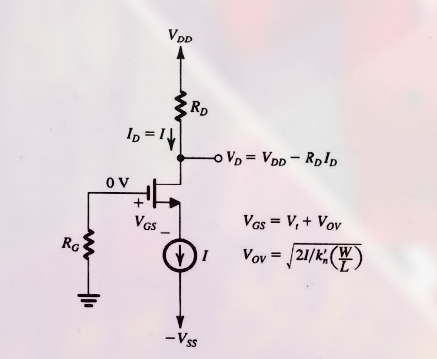
这里用 恒流源偏置 的策略.
4.7.2 放大器特性
判断共源, 共栅和共漏放大器的方法 : 去掉信号输入端, 从哪边往外取信号, 就是 “共” 另外一边的极. 或者, 在交流等效电路中哪个极接地就是 “共” 哪个极.
4.7.3 共源 (CS) 放大器
总结共源放大器的特征
CS 放大器具有
- 非常高的输入电阻
- 适中的电压增益, 反相放大器
- 相当高的输出电阻
共源 (CS) 或源极接地组态是使用最广泛的 MOSFET 放大器电路.
(什么是接地组态)
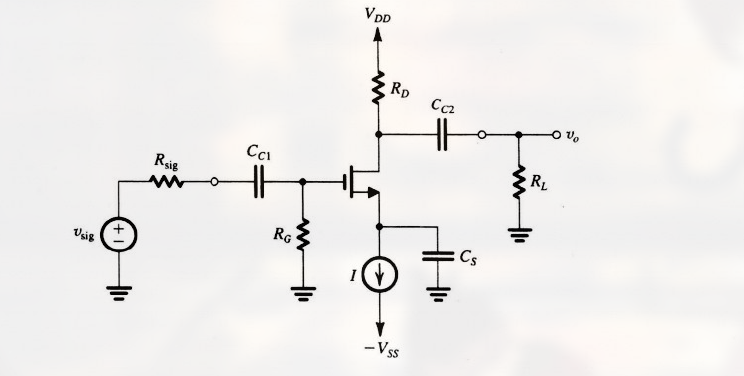
什么是 信号地 , 交流地 .
为了在源极建立信号地或通常所说的交流地, 在源极和地之间接上一个大电容 $C_S$, 该电容通常在 $\mu F$ 的范围, 并要求它在感兴趣的所有频率处具有非常小的阻抗 (理想情况下为 0 阻抗, 相当于短路)
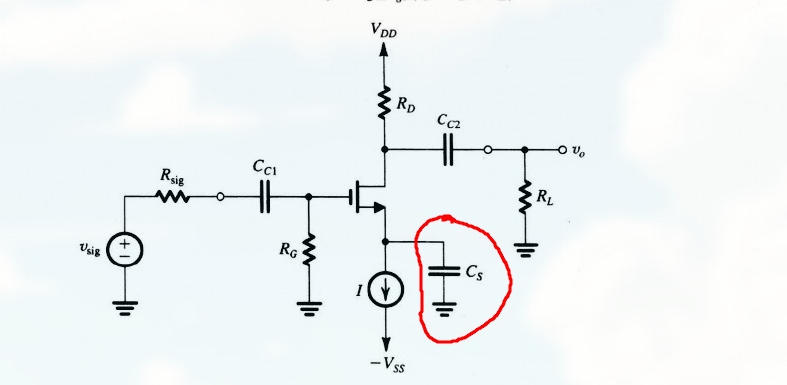
信号电流可以通过 $C_S$ 到地, 因此它旁路了(?)电流源 I (以及其他可能连接到 MOSFET 源极的任何电路元件) 的输出电阻, 因此, $C_S$ 被称为旁路电容
信号频率越低, 该旁路电容的有效性越低.
这里假定 $C_S$ 相当于 短路 , 因此在 MOSFET 源极建立一个 0 信号电压.
为了不干扰直流偏置电流和电压, 电压源 $v_{sig}$ 与内阻 $R_{sig}$ 的所要放大的信号 通过一个大电容 $C_{C1}$ 被连接到栅极.
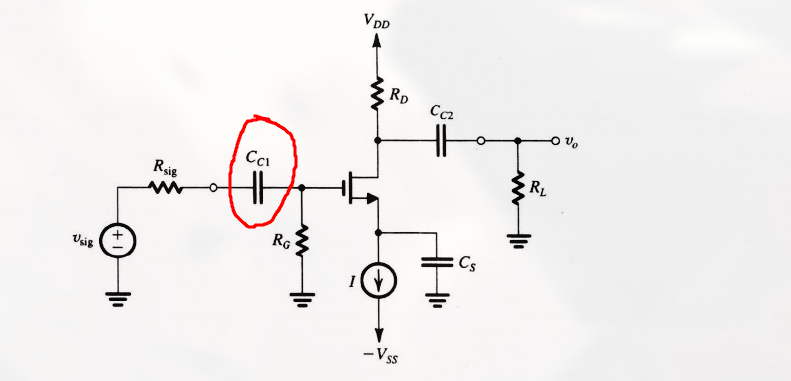
电容 $C_{C1}$ 被称为 耦合电容 , 其对所有感兴趣的信号频率呈短路 (也就是通过), 而对直流起隔断作用.
(为什么称为耦合电容)
在信号频率降低时, $C_{C1}$ 的阻抗会减小 ( $1/j\omega C_{C1}$, ? 不是增大么 ), 其作为耦合电容的作用会降低.
注意 , 在信号源能提供合适的到地的直流通路的情况下, 栅极可以直接连接到信号源, 并且 $R_G$ 和 $C_{C1}$ 可以略去.
在漏极产生的电压信号通过另一个耦合电容 $C_{C2}$ 耦合到负载电阻 $R_L$.
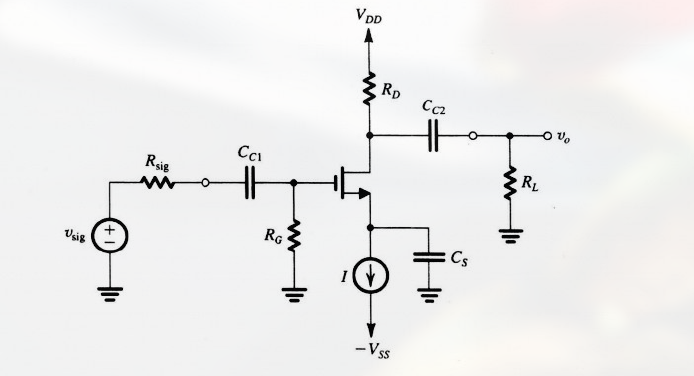
假定 $C_{C2}$ 对所有关心的信号都呈现短路, 因此输出电压:
$$
\displaylines
{
v_O = v_d
}
$$
( $v_d$ 是什么 )
确定 CS 放大器的端口特性
包括:
- 输入电阻
- 电压增益
- 输出电阻
用 小信号模型 来替代 MOSFET:
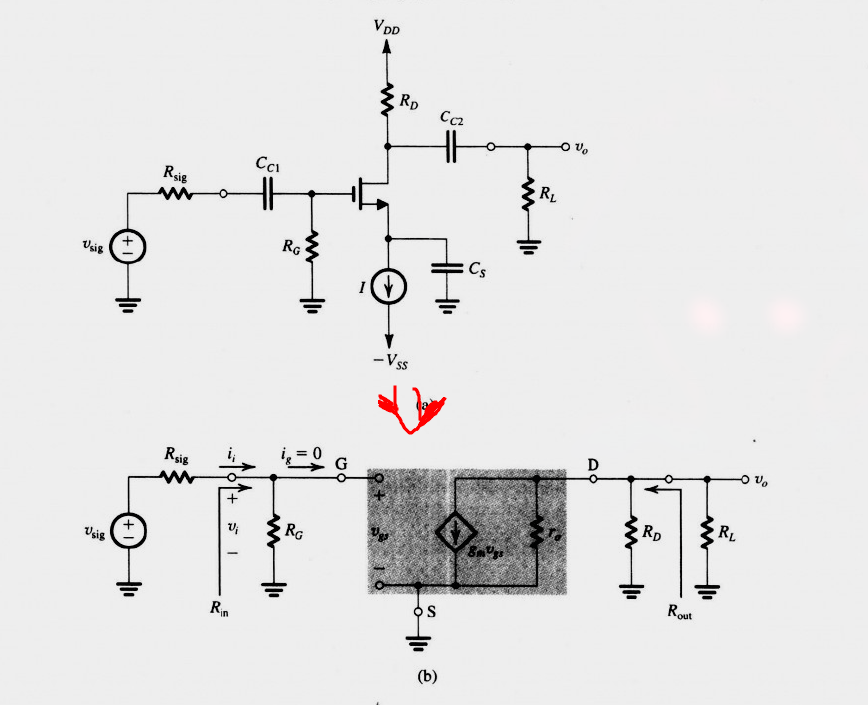
这里:
- 去掉了三个电容
- 标出了 MOSFET 的三个端口.
- 用 $v_{gs}$ 代替 $V_{DD}$ 和 $V_{SS}$ 和恒流源 (?)
此处:
$$
\displaylines
{
R_{in} = R_i \newline~ \newline
R_{out} = R_O
}
$$
分析
$$
\displaylines
{
i_g = 0 \newline~ \newline
R_{in} = R_G \newline~ \newline
v_i = v_{sig} \frac{R_{in}}{R_{in} + R_{sig}} \newline~ \newline
= v_{sig} \frac{R_G}{R_G + R_{sig}}
}
$$
通常有 $R_G \gg R_{sig}$ ( $R_G$ 为 $M\Omega$ 量级 ), 因此有:
$$
\displaylines
{
v_i \sim v_{sig} \newline~ \newline
v_{gs} = v_i \newline~ \newline
v_O = -g_m v_{gs} (r_O || R_D || R_L) \newline~ \newline
(v_O = i_O R, i_O = -g_m v_{gs}, R = r_O || R_D || R_L ) \newline~ \newline
电压增益 A_v: \newline~ \newline
A_v = -g_m (r_O || R_D || R_L) \newline~ \newline
(由 \frac{v_O}{v_{gs}} 得到) \newline~ \newline
开路电压增益 A_{VO}: \newline~ \newline
A_{VO} = -g_m (r_O || R_D) \newline~ \newline
从信号源到负载的总的电压增益为: \newline~ \newline
G_v = \frac{R_{in}}{R_{in} + R_{sig}} A_v \newline~ \newline
= -\frac{R_{in}}{R_{in} + R_{sig}}(r_O || R_D || R_L)
}
$$
(电压增益和开路电压增益有什么区别)
求放大器输出电阻 $R_{out}$
设 $v_{sig} = 0$, 有:
$$
\displaylines
{
R_{out} = r_O || R_D
}
$$
4.7.4 接源极电阻的共源放大器
在共源放大器的源极接入一个电阻 $R_S$ 通常非常有用 (后面有讲):
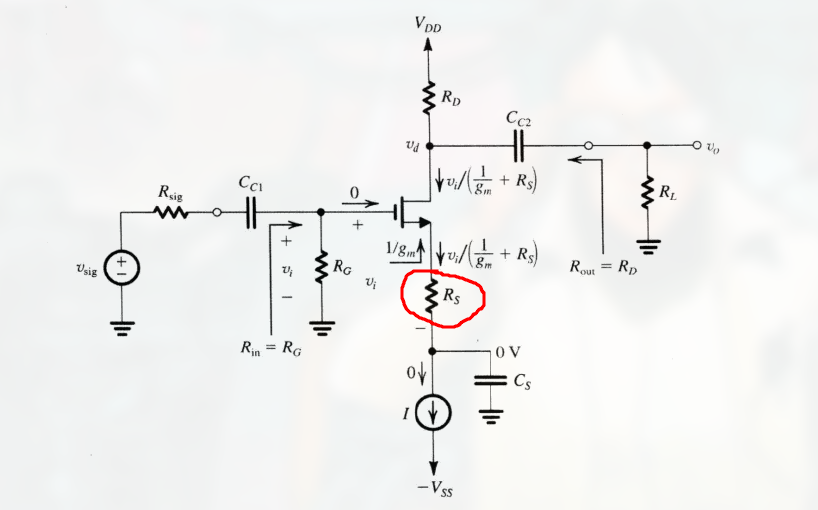
用 T 型等效电路模型替代得:
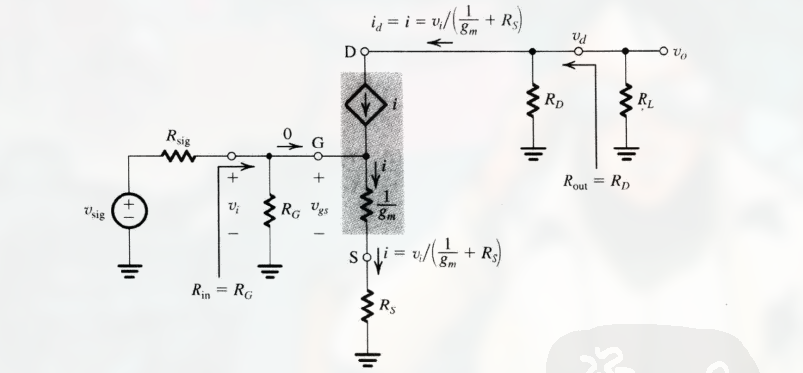
(这里忽略了 $r_O$, 已经证明了 $r_O$ 对分立元件电路放大器的影响并不重要)
分析端口特性
$$
\displaylines
{
R_{in} = R_i = R_G \newline~ \newline
v_i = v_{sig} \frac{R_G}{R_G + R_{sig}}
}
$$
此时 $v_{gs}$ 为 $v_i$ 的一部分:
$$
\displaylines
{
v_{gs} = v_i \frac{ \frac{1}{g_m} }{ \frac{1}{g_m} + R_s } \newline~ \newline
= \frac{v_i}{1 + g_m R_s}
}
$$
可以看出, 能够用 $R_S$ 的值来控制信号 $v_{gs}$ 的大小. $R_S$ 能提供负反馈, 但是会减小电压增益.
电流 $i_d$:
$$
\displaylines
{
i_d = i = \frac{v_i}{ \frac{1}{g_m} + R_S } \newline~ \newline
= \frac{g_m v_i}{1 + R_m R_S}
}
$$
输出电压 $v_O$:
$$
\displaylines
{
v_O = -i_d ( R_D || R_L ) \newline~ \newline
= - \frac{g_m (R_D || R_L)}{1 + g_m R_S} v_i
}
$$
电压增益 $A_V$:
$$
\displaylines
{
A_V = - \frac{g_m (R_D || R_L)}{1 + g_m R_S}
}
$$
(也可以理解为 从栅极到漏极的增益就是漏极的总电阻 $(R_D || R_L)$ 与源极的总电阻 $(1/g_m) + R_S$ 之比 )
若 $R_L = \infty$, 则有:
$$
\displaylines
{
A_V = - \frac{g_m R_D}{1 + g_m R_S}
}
$$
总电压增益 $G_V$:
$$
\displaylines
{
G_V = - \frac{R_G}{R_G + R_{sig}} \frac{g_m (R_D || R_L)}{1 + g_m R_S}
}
$$
$R_S$ 使 $i_d$ 减小, 而 $i_d$ 其实就是 $I_D$ 的变化量.
由于 $R_S$ 降低了增益, 因此称它为 源衰减电阻
4.7.5 共栅 (CG) 放大器
特点
- 较低输入电阻
- 同相放大器
将 MOSFET 的栅极接地可得到一个 共栅 (Common Gate) 或栅极接地放大器 .
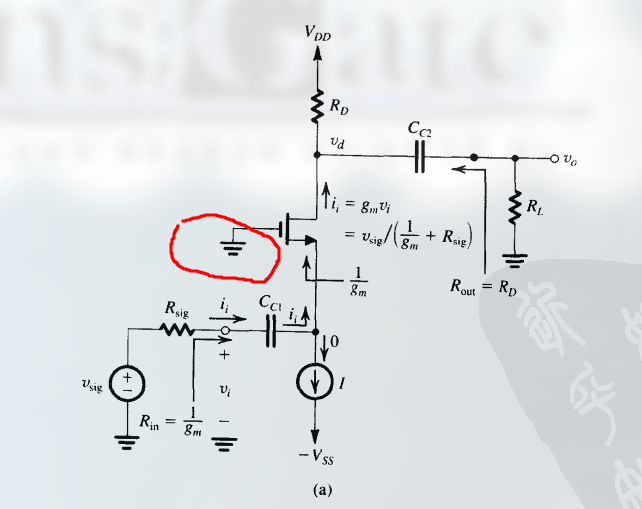
- 输入信号被加到源极
- 输出从 漏极 得到
- 栅极 成为输入和输出端口的 公共端 (这里可以把栅极看作一个端点)
其由下图变换而来:
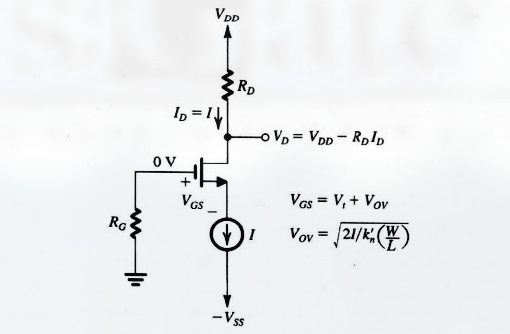
栅极处直流和交流电压都为 0, 可以直接将栅极接地, 同时也可以消除电阻 $R_G$.
CG 放大器中的 $C_{C1}$ 和 $C_{C2}$ 耦合电容的作用同样是: 对所有感兴趣的信号频率呈短路 (也就是通过), 而对直流起隔断作用.
CG 放大器的小信号等效电路模型 为 (这里为 T 模型):
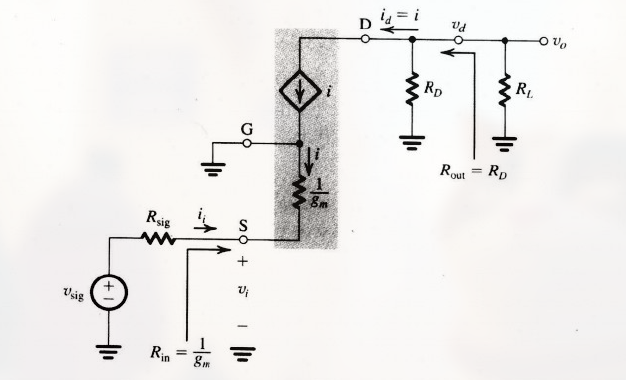
从这个模型可看出, 输入电阻为:
$$
\displaylines
{
R_{in} = \frac{1}{g_m}
}
$$
因为 $g_m$ 为 1mA/V 数量级, 因此 CG 放大器的输入电阻相对较低 (为 1 $k\Omega$ 数量级).
当信号耦合到 CG 放大器输入端时, 可能会造成较大的信号强度丢失, 因为:
$$
\displaylines
{
v_i = v_{sig} \frac{R_{in}}{R_{in} + R_{sig}}
}
$$
(可能是因为 $R_{in}$ 没有远大于 $R_{sig}$)
因此;
$$
\displaylines
{
v_i = v_{sig} \frac{ \frac{1}{g_m} }{ \frac{1}{g_m} + R_{sig} } \newline~ \newline
= v_{sig} \frac{1}{1 + g_m R_{sig}}
}
$$
可以看出, 为了减少信号强度的丢失, 源电阻 $R_{sig}$ 必须很小 :
$$
\displaylines
{
R_{sig} \ll \frac{1}{g_m}
}
$$
一些量的计算
可得出电流 $i_i$ :
$$
\displaylines
{
i_i = \frac{v_i}{R_{in}} = \frac{v_i}{1/g_m} = g_m v_i
}
$$
漏极电流 $i_d$:
$$
\displaylines
{
i_d = i = -i_i = -g_m v_i
}
$$
输出电压为:
$$
\displaylines
{
v_O = v_d = -i_d (R_D || R_L) = g_m (R_D || R_L) v_i
}
$$
电压增益为:
$$
\displaylines
{
A_V = g_m (R_D || R_L)
}
$$
开路电压增益:
$$
\displaylines
{
A_{VO} = g_m R_D
}
$$
总电压增益为:
$$
\displaylines
{
G_V = \frac{R_{in}}{R_{in} + R_{sig}}A_V = \frac{ \frac{1}{g_m} }{ \frac{1}{g_m} + R_{sig} }A_V = \frac{A_V}{1 + g_m R_{sig}} \newline~ \newline
= \frac{g_m (R_D || R_L)}{1 + g_m R_{sig}}
}
$$
输出电阻为:
$$
\displaylines
{
R_{out} = R_O = R_D
}
$$
共源放大器与共栅放大器的比较
- CS 放大器是反相放大器, CG 放大器为同相放大器
- CS 放大器有很高的输入电阻, 而 CG 放大器的输入电阻较低.
- CS 和 CG 放大器的 $A_V$ 值几乎相等, 而 CG 放大器的总电压增益要比 CS 放大器小 $1 + g_m R_{sig}$ 倍
CG 放大器的运行
用内阻为 $R_{sig}$ 的信号电流源 $i_{sig}$ 来激励 CG 放大器:
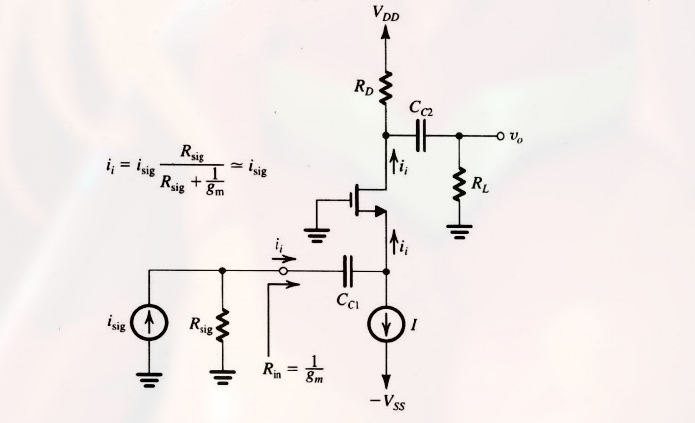
则, 流进 MOSFET 源极的电流 $i_i$:
$$
\displaylines
{
i_i = i_{sig} \frac{R_{sig}}{R_{sig} + R_{in}} \newline~ \newline
= i_{sig} \frac{R_{sig}}{R_{sig} + \frac{1}{g_m}} \newline~ \newline
( 利用电流分流以及 R_{in} = \frac{1}{g_m} )
}
$$
一般有 $R_{sig} \gg \frac{1}{g_m}$, 则有:
$$
\displaylines
{
i_i = i_{sig}
}
$$
可以得出, 当电路相对于输入信号电流源有相当低的输入电阻 $1/ g_m$, 使得输入端的信号电流衰减非常小
MOSFET 在漏极端重新产生这个电流, 并具有很大的输出电阻.
4.7.6 共漏或源极跟随放大器
特点
- 非常高的输入电阻
- 相当低的输出电阻
- 小于 1 但接近 1 的电压增益
该单极 MOSFET 放大器组态是在漏极上建立信号地, 并把它作为 栅极与漏极之间的输入端口和源极与漏极之间的输出端口的公共端 , 该电路叫做共漏放大器或漏极接地放大器, 也称源极跟随器.
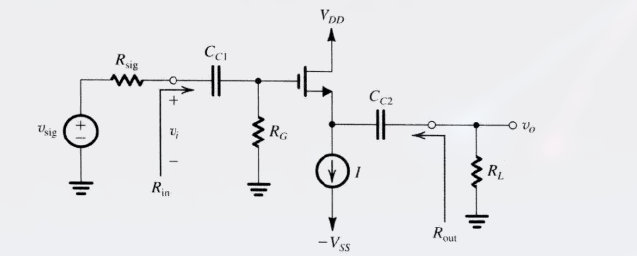
(信号地的含义似乎就是公共端口)
- 输入信号通过耦合电容 $C_{C1}$ 进入 MOSFET 栅极
- 在 MOSFET 源极的输出信号通过耦合电容 $C_{C2}$ 耦合到负载电阻 $R_L$
T 模型的共漏放大器的小信号等效电路为:
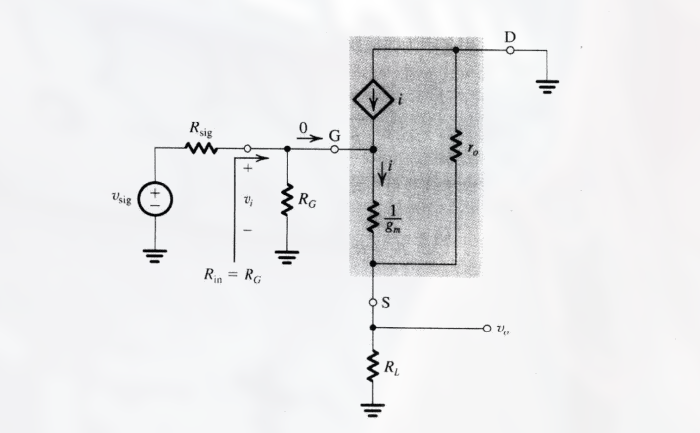
利用这个图来分析
输入电阻 $R_{in}$ 为:
$$
\displaylines
{
R_{in} = R_G
}
$$
输入信号:
$$
\displaylines
{
v_i = v_{sig} \frac{R_{in}}{R_{in} + R_{sig}} = v_{sig} \frac{R_G}{R_G + R_{sig}}
}
$$
通常 $R_{sig} \gg R_G$, 则:
$$
\displaylines
{
v_i \sim v_{sig}
}
$$
用电压分压法则来确定 $v_O$ 为:
$$
\displaylines
{
v_O = v_i \frac{R_L || r_O}{( R_L || r_O ) + \frac{1}{g_m}}
}
$$
电压增益 $A_v$ 为:
$$
\displaylines
{
A_v = \frac{R_L || r_O}{( R_L || r_O ) + \frac{1}{g_m}} \newline~ \newline
一般有, $r_O \gg R_L$, 因此: \newline~ \newline
A_v = \frac{R_L}{R_L + \frac{1}{g_m}}
}
$$
开路电压增益 $A_{vo}$ 为:
$$
\displaylines
{
A_{vo} = \frac{r_O}{r_O + \frac{1}{g_m}}
}
$$
通常 $r_O \gg 1/g_m$, 因此从栅极到源极的开路电压增益几乎为 1, 因此 源极电压跟随栅极电压而变 , 因此又被称为 源极跟随器 .
总电压增益 $G_V$ 为:
$$
\displaylines
{
G_V = \frac{R_G}{R_G + R_{sig}} \frac{R_L || r_O }{(R_L || r_O) + \frac{1}{g_m}} \newline~ \newline
当 R_G \gg R_{sig}, r_O \gg 1/g_m, r_O \gg R_L 时 \newline~ \newline
G_V \sim 1
}
$$
在 MOSFET 小信号模型的电路图上直接进行小信号分析来 确定输出电阻 :
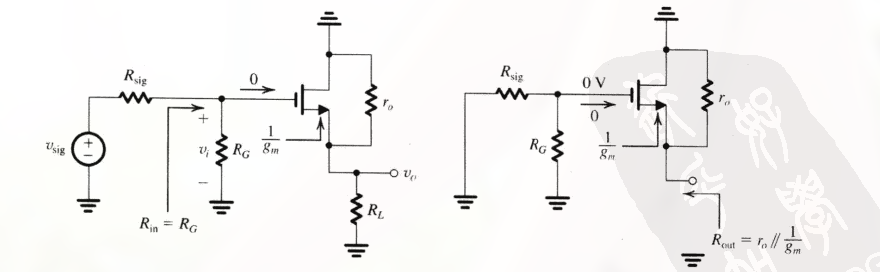
因为栅极电压为 0, 从源极看, 发现在源极和地之间电阻 $1/g_m$ 与 $r_O$ 并联:
$$
\displaylines
{
R_{out} = \frac{1}{g_m} || r_O \newline~ \newline
通常, r_O \gg 1/g_m, 因此: \newline~ \newline
R_{out} \sim \frac{1}{g_m}
}
$$
可以看出 $R_{out}$ 较低.
应用
把一个能提供合理大小的信号但具有高内阻的电压信号源连接到一个非常小的负载电阻, 也就是作为单位增益的 电压缓冲放大器
第6章 单级集成电路放大器
同时使用 MOS 管和 BJT 的电路被称为 BiMOS 或 BiCMOS 技术.
6.3 集成电路中的偏置 – 电流源, 镜像电流源及电流导向电路
6.3.1 MOSFET 基本电流源
一个简单的 MOSFET 恒流源如下:
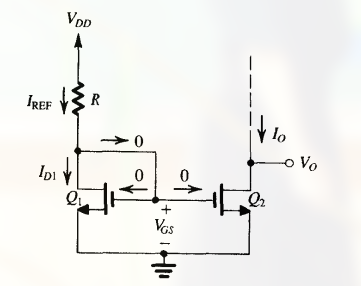
其核心为晶体管 $Q_1$, 其漏极与栅极短接, 因此其工作在饱和区.
对于 $Q_1$
有:
$$
\displaylines
{
I_{D1} = \frac{1}{2} k_n^\prime (\frac{W}{L}){2} ( V{GS} - V_{tn} )^2 \newline~ \newline
}
$$
(这里忽略了沟道长度调制效应)
同时:
$$
\displaylines
{
I_{D1} = I_{REF} = \frac{V_{DD} - V_{DS}}{R}
}
$$
通过 R 的电流被认为是电流源的参考电流, 记作 $I_{REF}$ (什么是参考电流, 其作用是什么)
对于 $Q_2$
- $V_{GS}$ 与 $Q_1$ 相等
若工作在饱和区, 即 $V_O \ge V_{OV}$, 则其漏极电流为:
$$
\displaylines
{
I_O = I_{D2} = \frac{1}{2} k_n^\prime ( \frac{W}{L} )2 ( V{GS} - V_{tn} )^2
}
$$
输出电流 $I_O$ 和参考电流 $I_{REF}$ 的关系为:
$$
\displaylines
{
\frac{I_O}{I_{REF}} = \frac{ (W/L)_2 }{ (W/L)_1 }
}
$$
当 两个晶体管完全一样时 , 有:
$$
\displaylines
{
(\frac{W}{L})_2 = (\frac{W}{L})_1
}
$$
即:
$$
\displaylines
{
I_O = I_{REF}
}
$$
电路在输出端简单地复制后镜像了参考电流, 此时, $Q_1$ 和 $Q_2$ 构成的电路被称为 镜像电流源.
这种 MOSFET 基本镜像电流源可以画为:
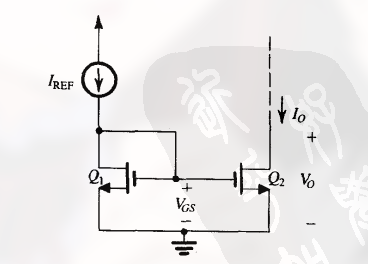
这里的条件为 $Q_2$为恒流源的输出端, 其需要保持饱和. 可以看出, 在输出电压 $V_O$ 低至 $V_{OV}$ 时, 电流源仍可正常工作.
当 考虑沟道长度调制效应 时, $Q_2$ 的漏极电流 $I_O$ 和 $Q_1$ 中的电流 $I_{REF}$ 都会 受到 $V_{DS}$ 的影响.
此时要让 $Q_2$ 的漏极电流 $I_O$ 与 $Q_1$ 中的电流 $I_{REF}$ 相等, 就需要使两个器件的 $V_{DS}$ 相等, 即:
$$
\displaylines
{
V_O = V_{GS}
}
$$
$I_O$ 随 $V_O$ 变化的关系图为:
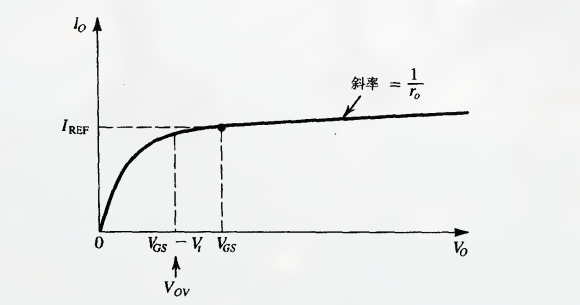
(可以看出在 $V_O = V_{GS}$ 时 $I_O = I_{REF}$)
上述两个电流源都有 有限大小的输出电阻 $R_O$ :
$$
\displaylines
{
R_O = \frac{\Delta V_O}{\Delta I_O} = r_{O2} = \frac{V_{A2}}{I_O}
}
$$
还可以把 $I_O$ 写为:
$$
\displaylines
{
I_O = \frac{(W/L)2}{(W/L)1} I{REF} ( 1 + \frac{V_O - V{GS}}{V_{A2}} )
}
$$
6.3.2 MOS 电流导向电路
把恒流源应用到集成电路的各级放大器以提供直流偏置电流.
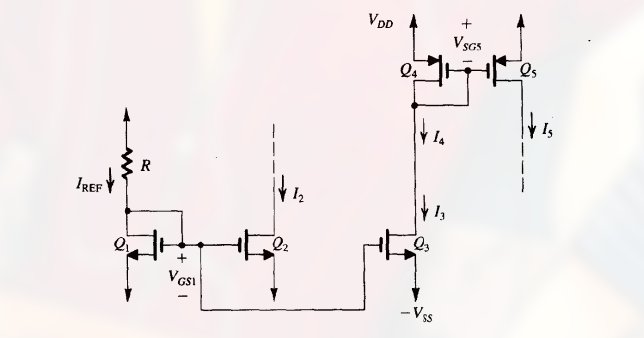
$Q_1$ 和 R 共同决定参考电流 $I_{REF}$, 晶体管 $Q_1$, $Q_2$ 和 $Q_3$ 构成了有两个输出端的镜像电流源.
(形成镜像电流源的条件)
有:
$$
\displaylines
{
I_2 = I_{REF} \frac{(W/L)_2}{(W/L)1} \newline~ \newline
I_3 = I{REF} \frac{(W/L)_2}{(W/L)_1}
}
$$
为了保证工作在饱和区, $Q_2$ 和 $Q_3$ 的漏端电压需满足:
$$
\displaylines
{
V_{D2}, V_{D3} \ge -V_{SS} + V_{GS1} - V_{tn} \newline~ \newline
即: \newline~ \newline
V_{D2}, V_{D3} \ge -V_{SS} + V_{OV1} \newline~ \newline
}
$$
( 驱动电压 $V_{OV}$ 通常是零点几伏)
$Q_4和Q_5$ 组成的镜像电流源提供的电流为:
$$
\displaylines
{
I_5 = I_4 \frac{ (W/L)_5 }{ (W/L)_4 } \newline~ \newline
I_4 = I_3
}
$$

为了让 $Q_5$ 保持工作在饱和区, 其漏端电压需满足:
$$
\displaylines
{
V_{DS} \le V_{DD} - \left\vert V_{OV5} \right\vert
}
$$
这里, $Q_5$ 将它的电流 $I_5$ 推入负载, 因此 $Q_5$ 被称为 电流源 , $Q_2$ 被称为 电流吸收器
第7章 差分放大器与多级放大器
7.1 MOS 差分对
MOS 差分对的基本结构如下:
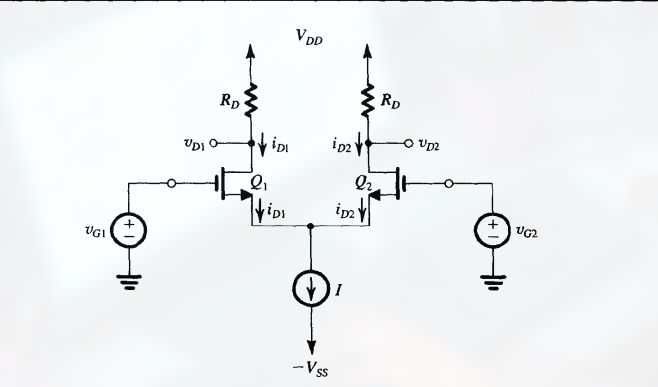
- 两个晶体管 $Q_1$ 和 $Q_2$ 的源极连接在一起
- 通过一个恒流源 I 提供偏置 (这里假设为理想恒流源, 输出电阻无穷大)
共模信号和差模信号
在差分放大器中,差模信号是指差分输入信号,也就是输入信号的两个分量的差,而共模信号是指两个分量的平均值。
具体来说,差分放大器有两个输入端口,分别为正输入($V_{in+}$)和负输入($V_{in-}$)。差模信号就是这两个输入信号的差,即 $V_{in+}-V_{in-}$。差分放大器的目的是放大这个差模信号。
而共模信号则是指这两个输入信号的平均值,即 $(V_{in+}+V_{in-})/2$。共模信号是差分放大器中的一种干扰,因为如果有共模信号存在,它会被放大器同时放大,从而影响系统的性能。
因此,差分放大器的一个重要特点是它可以抑制共模信号,只放大差模信号。这是通过将共模信号从放大器的输出中消除来实现的。一种常用的方法是使用差分放大器的输出来驱动一个反向相位的电路,从而将共模信号消除掉。
共模电压增益和差模电压增益
共模电压增益是指输入信号的共模分量经过放大器之后在输出信号中的增益。具体来说,如果 $V_{cm}$ 是输入信号的共模分量,$V_{out}$ 是放大器的输出信号,则共模电压增益 $A_{cm}$ 定义为:
$$ A_{cm} = \frac{V_{out}}{V_{cm}} $$
差模电压增益是指输入信号的差模分量经过放大器之后在输出信号中的增益。具体来说,如果 $V_{dm}$ 是输入信号的差模分量,则差模电压增益 $A_{dm}$ 定义为:
$$ A_{dm} = \frac{V_{out}}{V_{dm}} $$
差分放大器的设计目的是放大差模信号并抑制共模干扰。因此,差模电压增益是放大器性能的关键指标,它越大,放大器的放大能力就越强。而共模电压增益则是放大器的一个不良特性,因为它会将输入信号的共模分量放大并输出,从而影响系统的性能。
在理想情况下,差分放大器应该具有无穷大的差模电压增益和零的共模电压增益。在实际应用中,由于各种因素的影响,差分放大器的实际性能可能会受到影响。因此,设计和优化差分放大器的差模和共模增益是一个重要的工作。
7.1.1 共模电压输入下的工作特性
结论
当 $Q_1$ 和 $Q_2$ 处于饱和区时 , 电流 $I$ 始终会被 $Q_1$ 和 $Q_2$ 等分, 即漏极的电压保持不变, 差分对, 不对共模输入信号产生影响.
差分, 求的是 $v_{D1}$ 和 $v_{D2}$ 的差.
共模, 指的是两个 MOSFET 的栅极接在同一个电压上.
共模电压 (common mode voltage, 这里的 “模” 指 “模式”)为:

其中 两个栅极一同连接在电压 $v_{Cm}$ 上, 因此有:
$$
\displaylines
{
v_{G1} = v_{G2} = v_{CM}
}
$$
由于 $Q_1$ 和 $Q_2$ 是相同的晶体管, 因此:
$$
\displaylines
{
i_{D1} = i_{D2} = \frac{I}{2}
}
$$
(平分电流I)
源极电压 $v_S$ 为:
$$
\displaylines
{
v_S = v_{CM} - V_{GS}
}
$$
每个晶体管的漏极电压为:
$$
\displaylines
{
v_{D1} = v_{D2} = V_{DD} - \frac{I}{2} R_D
}
$$
此时两个漏极之间的电压差为零.
忽略沟道长度调制效应时, $V_{GS}$ 和 $I/2$ 的关系可以写为:
$$
\displaylines
{
\frac{I}{2} = \frac{1}{2} k_n^\prime \frac{W}{L} ( V_{GS} - V_t )^2 \newline~ \newline
= \frac{1}{2} k_n^\prime \frac{W}{L} V_{OV}^2 \newline~ \newline
V_{OV} = \sqrt{ I/k_n^\prime(W/L) }
}
$$
当 $Q_1$ 和 $Q_2$ 处于饱和区时 , 电流 $I$ 始终会被 $Q_1$ 和 $Q_2$ 等分, 即漏极的电压保持不变, 差分对, 不对共模输入信号产生影响.
共模输入的范围为:
$$
\displaylines
{
上限由 Q_1 和 Q_2 工作在饱和区决定: \newline~ \newline
v_{CMmax} = V_t + V_{DD} - \frac{I}{2} R_D \newline~ \newline
下限由电流源 I 正常工作所需要的电压决定, 若电流源需要的电压为 V_{CS}, 则: \newline~ \newline
v_{CM min} = -V_{SS} + V_{CS} + V_t + V_{OV}
}
$$
7.1.2 差模电压输入下的工作特性
施加一个差模电压, 如:
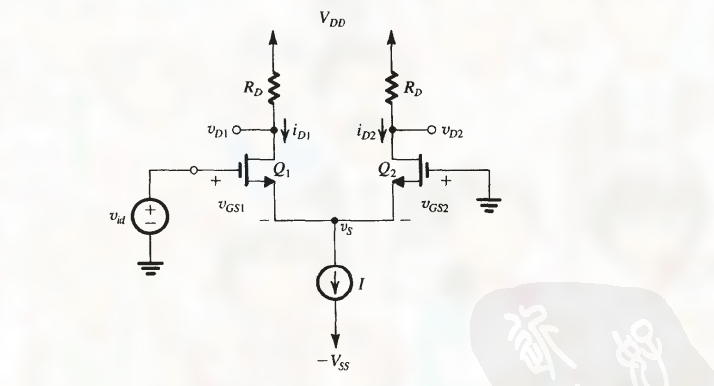
注意看和下图的共模输入的区别:

考虑当偏置电流 I 完全流过两个晶体管中的一个 的情况
此时需要:
- 一个 $v_{GS1}$ 使 $i_{D1} = I$
- $v_{G2} = -V_t$, 即 $v_S = -V_t$
即, $Q_2$ 刚刚开启, 此时没有电流通过, 因此流经最后电流源的电流只有 $Q_1$ 产生的电流.
计算 $v_{GS1}$
$$
\displaylines
{
\begin{aligned}
I = \frac{1}{2} ( k_n^\prime \frac{W}{L} ) ( v_{GS1} - V_t )^2 \newline~ \newline
v_{GS1} = V_t + \sqrt{ 2I / k_n^\prime (W/L) } \newline~ \newline
= V_t + \sqrt{2} V_{OV}
\end{aligned}
}
$$
计算 $v_{id\ max}$
$$
\displaylines
{
\begin{aligned}
v_{id\ max} = v_{GS1} + v_S \newline~ \newline
= V_t + \sqrt{2} V_{OV}
\end{aligned}
}
$$
(因为 $v_{GS1} = v_{id} - v_S$, 因此有 $v_{id} = v_{GS1} + v_S$)
可以得出 $v_{id}$ 的变化范围是:
$$
\displaylines
{
\begin{aligned}
-\sqrt{2} V_{OV} \le v_{id} \le \sqrt{2} V_{OV}
\end{aligned}
}
$$
(即差模输入的范围)
此时, 电流 I 来自两个晶体管.
但:
- 当 $v_{id} > \sqrt{2}V_{OV}$ 时, $i_{D1} = I$, 且 $v_{GS1}$ 始终等于 $V_t + \sqrt{2} V_{OV}$ (即 $v_{GS1}$ 不变), 因此 $v_S$ 增大 (因为 $v_{idmax} = v_{GS1} + v_S$, 一个增大, 另一个减小), 导致 $Q_2$ 截止
- 当 $v_{id} < -\sqrt{2}V_{OV}$ 时, $Q_1$ 截止, $Q_2$ 导通, 全部电流流过 $Q_2$
因此, 通过改变 $v_id$ 的值, 可以使电流 I 从一个晶体管流向另一个晶体管.
当把差分对作为 线性放大器使用 时, 需要确保输入信号 $v_{id}$ 是 一个小量 , 因此:
- 一个晶体管 ( $v_{id}$ 为正时, 是 $Q_1$ ), 流过的电流为 $\frac{I}{2} + \Delta I$, 增量电流 $\Delta I$ 与 $v_{id}$ 成正比
- 另一晶体管流过的电流为 $\frac{I}{2} - \Delta I$
由于, 增量电流
- 在前者漏端产生 $-\Delta I R_D$ 的信号电压
- 在另一个漏端产生相反方向的信号电压 $\Delta I R_D$
因此, 从两个漏极间获得的输出信号电压 为 $2\Delta I R_D$, 同样正比于差模输入 $v_id$.
7.1.3 大信号工作特性
这里推导差模输入信号 $v_{id} = v_{G1} - v_{G2}$ 表示的漏极电流 $i_{D1}$ 和 $i_{D2}$ 的表达式.
假设 $Q_1$ 和 $Q_2$ 始终不工作在变阻区, 且忽略沟道长度调制效应 ( $\lambda = 0$ ) 和衬底效应.
如下图:
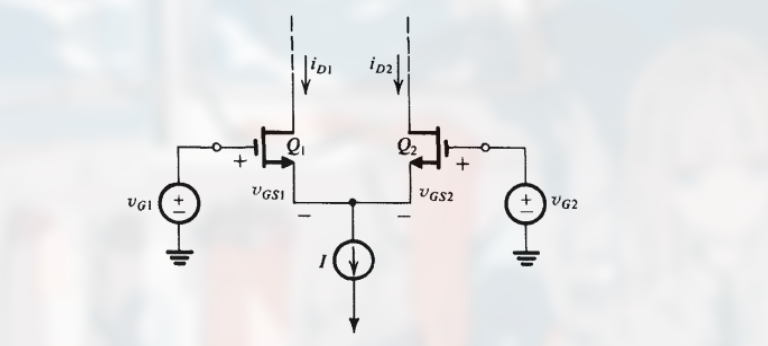
有 $Q_1$ 和 $Q_2$ 的漏极电流表达式:
$$
\displaylines
{
\begin{aligned}
i_{D1} = \frac{1}{2} k_n^\prime \frac{W}{L} ( v_{GS1} - V_t )^2 \newline~ \newline
i_{D2} = \frac{1}{2} k_n^\prime \frac{W}{L} ( v_{GS2} - V_t )^2
\end{aligned}
}
$$
($v_{GS} - V_{t} = V_{OV}$)
开方得:
$$
\displaylines
{
\begin{aligned}
\sqrt{i_D1} = \sqrt{ \frac{1}{2} k_n^\prime \frac{W}{L} } (v_{GS1} - V_t) \newline~ \newline
\sqrt{i_D2} = \sqrt{ \frac{1}{2} k_n^\prime \frac{W}{L} } (v_{GS2} - V_t)
\end{aligned}
}
$$
两式相减且带入 $v_{GS1} - v_{GS2} = v_{G1} - v_{G2} = v_{id}$ 得:
$$
\displaylines
{
\begin{aligned}
\sqrt{i_D1} - \sqrt{i_{D2}} = \sqrt{ \frac{1}{2}k_n^\prime \frac{W}{L} v_{id} }
\end{aligned}
}
$$
且有:
$$
\displaylines
{
\begin{aligned}
i_{D1} + i_{D2} = I
\end{aligned}
}
$$
当偏置(静态)工作点上的 $v_{id} = 0$ 时, 可以推出:
$$
\displaylines
{
\begin{aligned}
i_{D1} = i_{D2} \frac{I}{2} \newline~ \newline
即: \newline~ \newline
v_{GS1} = v_{GS2} = V_{GS}
\end{aligned}
}
$$
由:
$$
\displaylines
{
\begin{aligned}
\frac{I}{2} = \frac{1}{2} k_n^\prime \frac{W}{L} ( V_{GS} - V_t )^2 = \frac{1}{2} k_n^\prime \frac{W}{L} V_{OV}^2
\end{aligned}
}
$$
可以推导出:
$$
\displaylines
{
\begin{aligned}
i_{D1} = \frac{I}{2} + ( \frac{I}{V_{OV}} )( \frac{v_{id}}{2} ) \sqrt{1 - ( \frac{v_{id}/2}{V_{OV}} )^2} \newline~ \newline
i_{D2} = \frac{I}{2} - ( \frac{I}{V_{OV}} )( \frac{v_{id}}{2} ) \sqrt{1 - ( \frac{v_{id}/2}{V_{OV}} )^2} \newline~ \newline
\end{aligned}
}
$$
(注意, 一个是 +, 一个是 -)
其描述了:
- 当 $v_{id} = 0$ 时, 两个电流均为 $I/2$
- 当 $v_{id}$ 正值增加, $i_{D1}$ 增大的部分和 $i_{D2}$ 减少的部分相等, 始终保持 $i_{D1} + i_{D2} = I$
- 当 $v_{id}$ 达到 $\sqrt{2} V_{OV}$ 时, 电流全部流经 $Q_1$
- 若 $v_{id}$ 为负值, 将上述 $Q_1$ 和 $Q_2$ 调换
上述的传输特性为 非线性的, 因为包含 $v_{id}^2$ 项, 当 $v_{id}$ 尽可能小时, 可以得到:
$$
\displaylines
{
\begin{aligned}
i_{D1} = \frac{I}{2} + ( \frac{I}{V_{OV}} ) ( \frac{v_{id}}{2} ) \newline~ \newline
i_{D2} = \frac{I}{2} - ( \frac{I}{V_{OV}} ) ( \frac{v_{id}}{2} )
\end{aligned}
}
$$
变化的部分 $i_d$ 正比于差模输入信号 $v_{id}$:
$$
\displaylines
{
\begin{aligned}
i_d = ( \frac{I}{V_{OV}} ) ( \frac{v_{id}}{2} )
\end{aligned}
}
$$
这里的 $\frac{I}{V_{OV}}$ 也是 MOSFET 的跨导 $g_m = 2I_D/V_{OV}$ ( $I = 2I_D$ )
电压值为 $\frac{v_{id}}{2}$ 是因为 $v_{id}$ 被平均分配给了两个晶体管器件, $v_{gs1} = v_{id}/2$, $v_{gs2} = -v_{id}/2$
线性度和跨导二者不可兼得: 增加 $V_{OV}$ (即采用更小的 W/L 器件) 可以扩大线性范围, 但 $g_m$ 和增益会减小.
7.2 MOS 差分对的小信号工作特性
7.2.1 差模增益
观察下图:
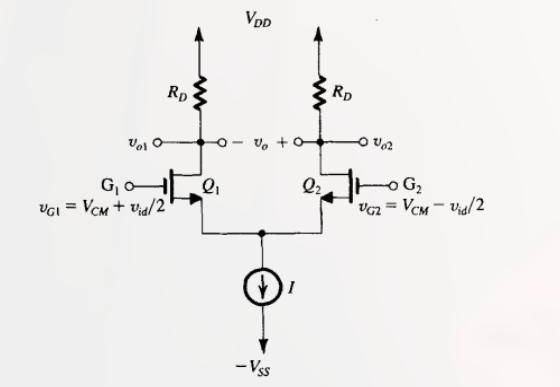
MOS 差分对的输入电压为:
$$
\displaylines
{
\begin{aligned}
v_{G1} = V_{CM} + \frac{1}{2} v_{id} \newline~ \newline
v_{G2} = V_{CM} - \frac{1}{2} v_{id}
\end{aligned}
}
$$
( $V_{CM}$ 是在共模输入范围内的共模直流电压, 其用来设置 MOSFET 栅极的直流电压 )
这里的差模输入电压 $v_{id}$ 以互补的方式接入, 即 $v_{G1}$ 增加 $v_{id}/2$ 的同时 $v_{G2}$ 会减少 $v_{id}/2$.
(为什么一个增大另一个会减小)
在这个图中:

放大器的输出可以取自:
- 某个晶体管的漏极和地之间, 即 单端输出 , 此时 $v_{o1}$ 和 $v_{o2}$ 是叠加在漏极直流电压 $V_{DD} - \frac{I}{2}R_D$ 之上的 (也就是说, 输出之中即有直流分量, 也有交流分量)
- 两个漏极之间, 即 双端输出 此时的输出电压完全由信号分量构成
旁路电容
旁路电容(decoupling capacitor)是一种被广泛用于电子电路中的电容器,其主要作用是在电路中提供稳定的电源电压和抑制电源噪声。
在电子电路中,由于各个电子元件的存在,电路中会存在各种噪声和干扰,这些噪声和干扰会对电路的稳定性和性能产生负面影响。旁路电容器的作用就是通过对电源电压进行滤波,阻止高频噪声的传播和抑制电源的另一种干扰,从而提高电路的稳定性和性能。
旁路电容通常被连接在电路元件的电源引脚上,与电源形成一个并联电路。当电源电压发生变化时,旁路电容器可以提供一定的电流响应,稳定电源电压。另外,旁路电容器的电容值也可以根据电路的需求进行选择,以提供不同的滤波效果
这里分析小信号的工作特性, 因此除去直流电源和 $V_{CM}$ (为什么) 得:
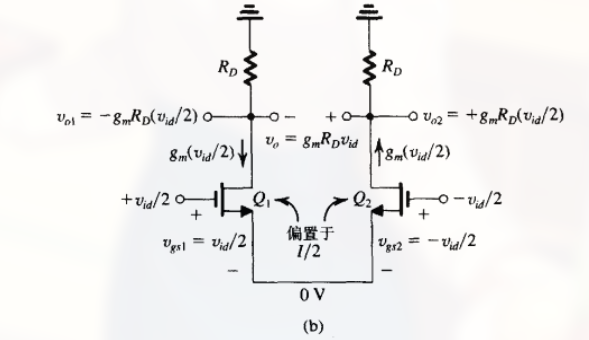
假设 $v_{id}/2 \ll V_{OV}$, 此时满足小信号近似条件, 因此有:
- $Q_1$ 和 $Q_2$ 的漏极电流的变化量分别正比于 $v_{gs1}$ 和 $v_{gs2}$
两个晶体管的跨导为:
$$
\displaylines
{
\begin{aligned}
g_m = \frac{2I_D}{V_{OV}} = \frac{2(I/2)}{V_{OV}} = \frac{I}{V_{OV}}
\end{aligned}
}
$$
若简单认为两个电流信号通过一对匹配的电阻 $R_D$, 可以得出漏极的电压信号为:
$$
\displaylines
{
\begin{aligned}
v_{o1} = -g_m \frac{v_{id}}{2} R_D \newline~ \newline
v_{o2} = +g_m \frac{v_{id}}{2} R_D
\end{aligned}
}
$$
此时:
取单端输入, 增益有:
$$
\displaylines
{
\begin{aligned}
\frac{v_{o1}}{v_{id}} = - \frac{1}{2} g_m R_D \newline~ \newline
\frac{v_{o2}}{v_{id}} = \frac{1}{2} g_m R_D
\end{aligned}
}
$$取差分输出 (双端输出), 增益有:
$$
\displaylines
{
\begin{aligned}
A_d = \frac{v_{o2} - v_{o1}}{ v_{id} } = g_m R_D
\end{aligned}
}
$$
可以看出取差分输出时增益更大.
一个事实
MOSFET 从源极视入的栅极和源极之间的等效电阻为 $1/g_m$ (也就是 R)
$G_1$ 和 $G_2$ 之间位于源极的总电阻为 $2/g_m$, 因此电流 $i_d$ 可以通过 $v_{id}$ 除以 $2/g_m$ 得到
7.2.2 共模增益与共模抑制比
如下图:
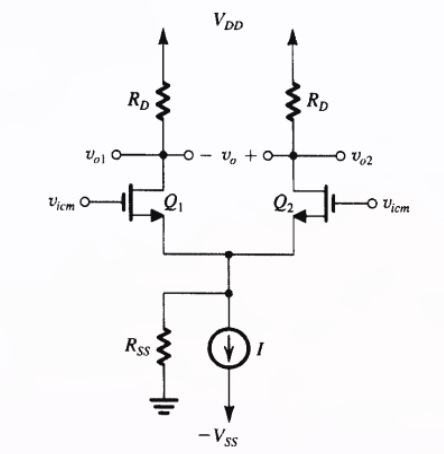
这里的 $v_{icm}$ (input common mode) 代表作用域两输入端的噪声或干扰信号. 且输入端的直流分量 $V_{CM}$ 没有画出.
由于电路的对称性, 该电路可以分成相同的两半, 如:
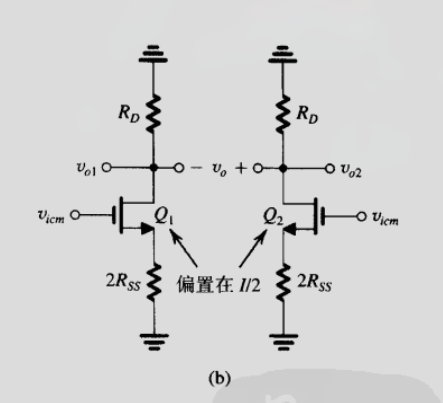
( 被称为 共模半电路 )
忽略电阻 $r_o$ 的影响时, 可以写出半电路的电压增益为:
$$
\displaylines
{
\begin{aligned}
\frac{v_{o1}}{v_{icm}} = \frac{v_{o2}}{v_{icm}} = - \frac{R_D}{ \frac{1}{g_m} + 2R_{SS} }
\end{aligned}
}
$$
通常 $R_{SS} \gg 1/g_m$, 因此有:
$$
\displaylines
{
\begin{aligned}
\frac{v_{o1}}{v_{icm}} = \frac{v_{o2}}{v_{icm}} = -\frac{R_D}{2R_{SS}}
\end{aligned}
}
$$
两种情况:
差分对的输出是单端的:
$$
\displaylines
{
\begin{aligned}
\left\vert A_{cm} \right\vert = \frac{R_D}{2 R_{SS}} \newline~ \newline
\left\vert A_d \right\vert \frac{1}{2} g_m R_D
\end{aligned}
}
$$
共模抑制比为:
$$
\displaylines
{
\begin{aligned}
CMRR = \left\vert \frac{A_d}{A_{cm}} \right\vert = g_m R_{SS}
\end{aligned}
}
$$差分对的输出是差分对:
$$
\displaylines
{
\begin{aligned}
A_{cm} = \frac{v_{o2} - v_{o1}}{v_{icm}} = 0 \newline~ \newline
A_d = \frac{v_{o2} - v_{o1}}{v_{id}} = g_m R_D \newline~ \newline
CMRR = \infty
\end{aligned}
}
$$
R_D 失配对 CMRR 的影响 , 见书.
g_m 失配对 CMRR 的影响 , 见书.
7.5 有源负载差分放大器
采用恒流源代替电阻 $R_D$ 不仅可以极大提高放大器的电压增益, 同时还可以节省芯片面积.
7.5.1 差分输出到单端输出的转变
输出取自两个漏极 (或集电极) 之间的电压能够使差模增益的数值加倍, 同时共模增益大大减小.
注意 , 唯一导致共模输入在差分对中产生输出电压的原因就是 电路会不可避免的失配
为了使多级放大器能够获得很高的 CMRR, 第一级的输出必须采用差分形式.
一种基本的从差分到单端转变的方法 :
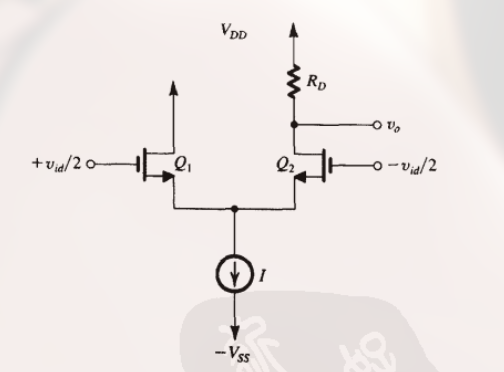
- 忽略 $Q_1$ 漏极的电流信号, 同时去掉其漏极电阻
- 输出取自 $Q_2$ 的漏极和地之间
其缺点为 , 增益损失了两倍.
7.5.2 有源负载 MOS 差分对
如图:
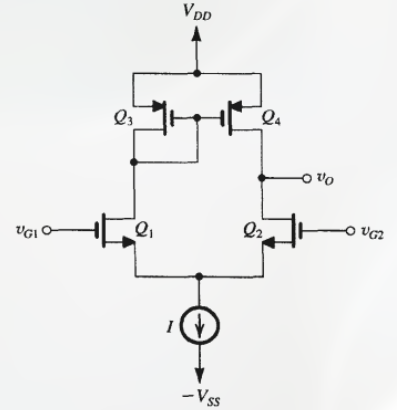
其中, $Q_3$ 和 $Q_4$ 的栅极相连, 且为 0V, 即输入电压为 0V.
注意, $Q_3$ 和 $Q_4$ 是 PMOS, 因此上方是源极, 由 $V_{DD}$ 提供偏置. 在 $Q_3$ 和 $Q_4$ 栅极之间的导线用于让 $Q_3$ 处于饱和区 $V_{GD} = 0 < V_t$,
当电路完全匹配时, 偏置电流 I (电流源的电流) 被 $Q_1$ 和 $Q_2$ 平分, 如:
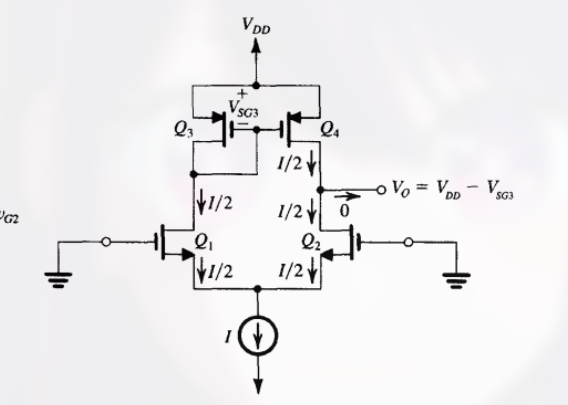
在输出节点处, 两个节点的电流均为 $I/2$, 导致输出给下一级或负载的电流为零. 但由于实际电路会失配, 因此会产生净电流.
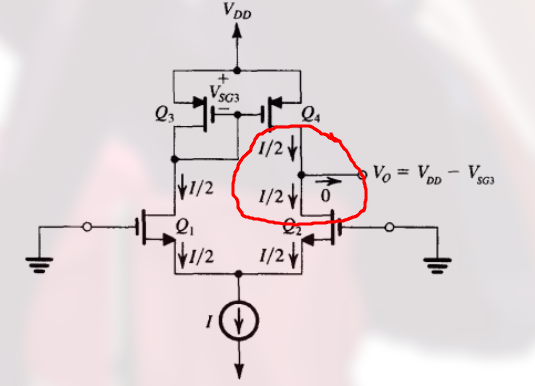
当 $Q_4$ 和 $Q_3$ 完全匹配时, $Q_4$ 的漏极电压等同于 $Q_3$ 的漏极电压, 此时输出电压为:
$$
\displaylines
{
\begin{aligned}
V_O = V_{DD} - V_{SG3}
\end{aligned}
}
$$
(为什么只考虑小信号特性时, 要去掉直流电源, 而且为什么能忽略 $r_O$ 的影响)
考虑小信号特性
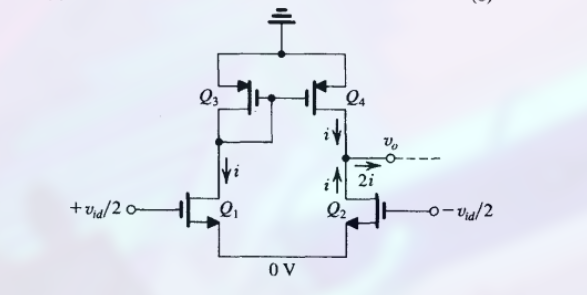
对于 $Q_1$ 和 $Q_2$:
- $Q_1$ 端输入 $+v_{id}/2$, 而 $Q_2$ 端输入 $-v_{id}/2$, 导致电流等大反向 $i = g_m v_{id}/2$
同时, $Q_1$ 的信号电流作为 $Q_3$ 和 $Q_4$ 镜像电流源的输入:
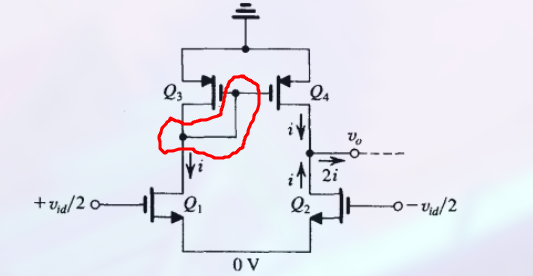
导致:
- $Q_4$ 输出镜像电流 i
此时 电路在不损失增益的情况下将输出信号改为单端形式 (输出电流此时为 2i)
第8章 反馈
反馈可分为:
- 负反馈 (衰减电路)
- 正反馈 (再生电路)
性能的改善如:
- 降低增益灵敏度
- 减小非线性失真
- 降低噪声的影响
- 控制输入和输出阻抗
- 扩展放大器的带宽
都是以降低增益为代价. 也就是 负反馈的基本思想, 以牺牲增益来换取其他方面的性能改善.
增益降低的倍数称为 反馈深度.
在某些情况下, 放大器中的负反馈可能会转化为正反馈, 且在幅度达到一定值时产生振荡.
8.1 反馈放大器的基本结构
如下图:
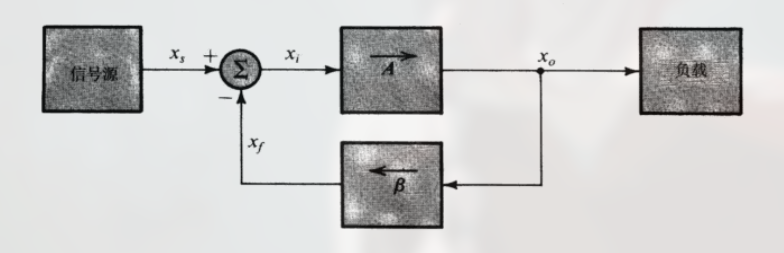
该图没有明确标明电流和电压信号, 而是 信号流 的形式, 每一个变量 x 代表一个电流或电压信号.
假设放大器的 开环增益 为 A, 则其输出 $x_O$ 与输入 $x_i$ 的关系为:
$$
\displaylines
{
\begin{aligned}
x_O = A x_i
\end{aligned}
}
$$
什么是开环增益
开环增益是一个系统或电路的输出与输入之间的增益,而没有考虑反馈回路的影响。在一个开环系统中,输出信号的大小和输入信号的大小是直接相关的,而不考虑系统内部的各种变化和干扰。因此,开环增益可以被认为是系统或电路的理论最大增益。
也就是, 将反馈看作一个环, 没有反馈时的增益就是开环增益.
输出信号 $x_O$ 会同时对:
- 负载
- 反馈网络
其作用.
因此反馈网络会产生一个 采样输出 $x_f$ , 若反馈网络的反馈系数为 $\beta$, 则 $x_O$ 和 $x_f$ 的关系为:
$$
\displaylines
{
\begin{aligned}
x_f = \beta x_o
\end{aligned}
}
$$
此时, 基本放大器的净输入信号 $x_i$ 就等于整个反馈放大器的源输入信号 $x_s$ 减去反馈信号 $x_f$:
$$
\displaylines
{
\begin{aligned}
x_i = x_s - x_f
\end{aligned}
}
$$
(可以看出, 负反馈的本质就是减小基本放大器的净输入信号)
结合:
$$
\displaylines
{
\begin{aligned}
\begin{cases}
x_O = Ax_i \newline~ \newline
x_i = x_s - x_f
\end{cases}
\end{aligned}
}
$$
可求得反馈放大器的增益为:
$$
\displaylines
{
\begin{aligned}
A_f = \frac{x_O}{x_s} = \frac{A}{1 + A\beta}
\end{aligned}
}
$$
( $A_f$ 中的 f 应该是指 “feedback” )
这里的 $A \beta$ 被称为 环路增益
对于负反馈而言, 环路增益 $A\beta$ 应为 正值 . ( 此时 $x_f$ 和 $x_s$ 同号, 形成的 $x_i$ 会是一个较小的差值信号 )
而当 $A \beta$ 为正时, 反馈放大器的增益 $A_f$ 比其开环增益小 $1 + A\beta$ 倍, 而这里的 $1 + A\beta$ 也被称为 反馈深度.
当环路增益 $A \beta$ 足够大时, 即 $A \beta \gg 1$, 则有:
$$
\displaylines
{
\begin{aligned}
A_f = \frac{A}{1 + A\beta} \newline~ \newline
变为: \newline~ \newline
A_f = \frac{A}{A \beta} = \frac{1}{\beta}
\end{aligned}
}
$$
即, 反馈放大器的增益几乎完全由反馈网络决定. 也就是说, 整个放大器的总增益几乎与基本放大器的增益 A 无关.
反馈信号 $x_f$ 的表达式
结合:
$$
\displaylines
{
\begin{aligned}
\begin{cases}
x_O = Ax_i \newline~ \newline
x_f = \beta x_O
\end{cases}
\end{aligned}
}
$$
得:
$$
\displaylines
{
\begin{aligned}
x_f = \frac{A \beta}{1 + A\beta}x_s
\end{aligned}
}
$$
当 $A \beta \gg 1$ 时, 有:
$$
\displaylines
{
\begin{aligned}
x_f \approx x_s
\end{aligned}
}
$$
即, 基本放大器输入信号 $x_i$ 接近于零. 其表现出两输入端的 跟踪效应 , 即反馈信号 $x_f$ 将几乎完全复制输入信号 $x_s$.
此时 $x_s$ 和 $x_f$ 之间的差值 $x_i$ 有时也被称为 误差信号 .
基本放大器的输入信号 $x_i$
$$
\displaylines
{
\begin{aligned}
x_i = \frac{1}{1 + A\beta} x_s
\end{aligned}
}
$$
8.2 负反馈的一些性质
8.2.1 降低增益灵敏度
增益灵敏度指, 基本放大器下降一定比例后, 对闭环放大器的影响程度.
已知:
$$
\displaylines
{
\begin{aligned}
A_f = \frac{x_O}{x_S} = \frac{A}{1 + A\beta}
\end{aligned}
}
$$
$A$ 为基本放大器增益, $A_f$ 为闭环增益.
则, 对其求导得:
$$
\displaylines
{
\begin{aligned}
dA_f = \frac{dA}{( 1 + A \beta )^2} \newline~ \newline
除以上边的式子得: \newline~ \newline
\frac{dA_f}{A_f} = \frac{1}{(1 + A\beta)} \frac{dA}{A}
\end{aligned}
}
$$
可以看出, $A_f$ 的相对变化比 A 的相对变化小 $(1+A \beta)$ (反馈深度) 倍, 因此反馈深度 $(1+ A\beta)$ 也被称为 灵敏度衰减因子.
8.2.2 扩展带宽
放大器的, 中频增益, 和, 高频增益函数为:
$$
\displaylines
{
\begin{aligned}
A(s) = \frac{A_M}{1 + s/\omega_H}
\end{aligned}
}
$$
( $A_M$ 为中频区增益, $\omega_H$ 是上限 3dB 频率 )
什么是中频增益.
反馈放大器的闭环增益函数 $A_f(S)$ 为:
$$
\displaylines
{
\begin{aligned}
A_f(s) = \frac{A(s)}{ 1 + \beta A(s) }
\end{aligned}
}
$$
结合两式可得到:
$$
\displaylines
{
\begin{aligned}
A_f (s) = \frac{A_M / (1 + A_M \beta)}{1 + s/\omega_H(1 + A_M \beta)}
\end{aligned}
}
$$
因此, 反馈放大器的中频增益为 $A_M/(1+A_M \beta)$, 上限 3dB 频率 $\omega_{Hf}$ 为:
$$
\displaylines
{
\begin{aligned}
\omega_{Hf} = \omega_H (1 + A_M \beta)
\end{aligned}
}
$$
反馈放大器闭环增益的下限频率 $\omega_{Lf}$ 为:
$$
\displaylines
{
\begin{aligned}
\omega_{L f} = \frac{\omega_L}{1 + A_M \beta}
\end{aligned}
}
$$
8.2.3 降低噪声
8.2.4 减小非线性失真
8.3 四种基本的反馈拓扑图
8.3.1 电压放大器
功能
放大电压输入信号并输出相应的电压信号.
实质
压控电压源.
要求
- 高输入阻抗
- 低输出阻抗
因此其拓扑图如:
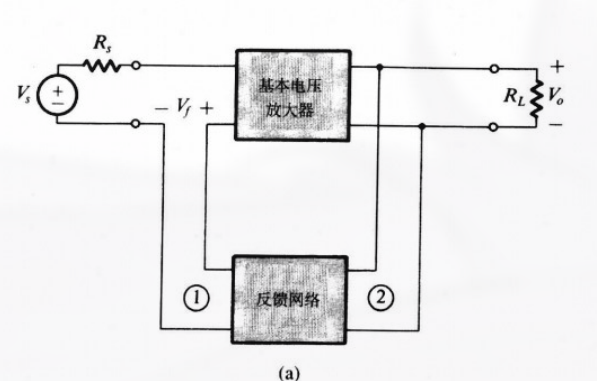
- 输入端为串联连接.
- 输出端为并联连接
该反馈拓扑结构也称为 串联-并联反馈
用 戴维南等效电路 分析, 反馈网络采样输出电压.
8.3.2 电流放大器
功能
放大 电流输入信号 并输出相应的电流信号.
要求
- 低输入电阻
- 高输出电阻
其拓扑图为:
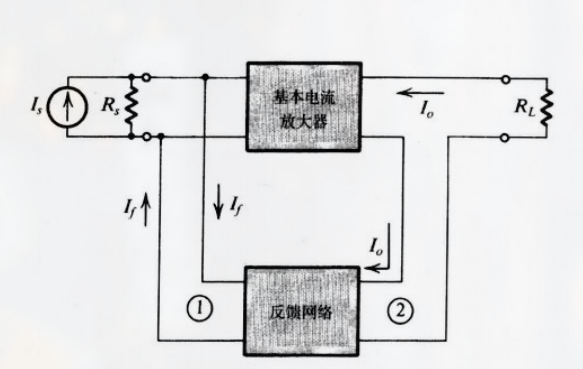
- 输入端并联连接
- 输出端串联连接
被称为 并联-串联反馈.
由于采样为 输出电流, 该反馈拓扑结构也被称为 电流混合电流采样拓扑结构 .
反馈极性的分析方法 (判断是正反馈还是负反馈)
用 沿环路跟踪信号 来分析.
如:
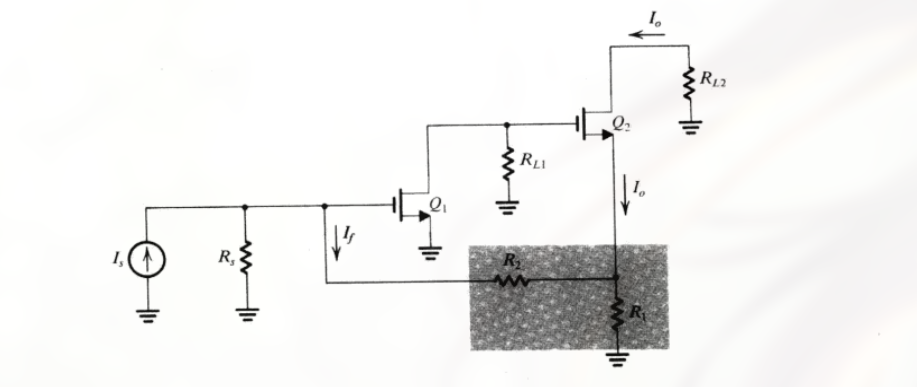
- 假设 $I_S$ 增大
- $Q_1$ 的栅极电压会随之增大, 漏极电流同时增大
- 导致 $Q_1$ 的漏极电压减小, $Q_2$ 的漏极电流 $I_O$ 减小, $Q_2$ 的源极电流 $I_O$ 也会减小
- $I_O$ 减小会导致 $I_f$ 增加, 而 $I_f$ 增加会削减输入信号 $I_s$ 的幅度, 使放大器净输入量的增加幅度减小
- 综上判定为 负反馈
8.3.3 互导放大器
功能
放大 电压入信号 并输出相应的电流信号.
其拓扑图为:
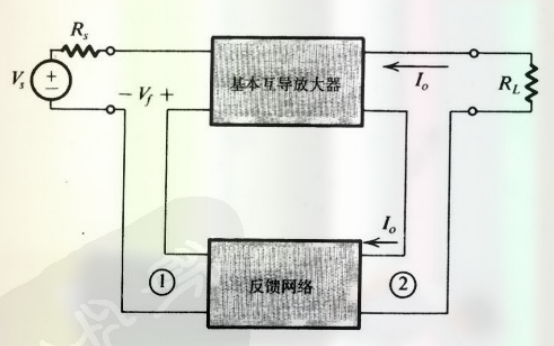
- 输入端串联
- 输出端串联
因此被称为 串联-串联反馈 .
由于输入为电压信号, 采样为电流信号, 其也被称为 电压混合电流采样拓扑结构 .
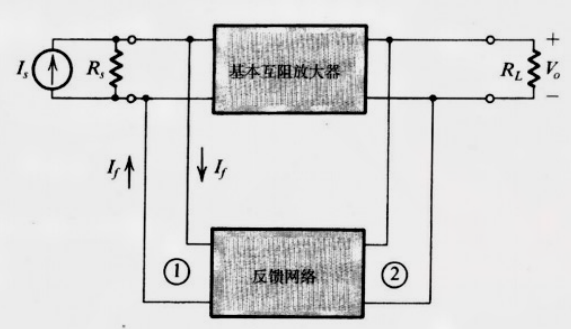
8.3.4 互阻放大器
功能
放大 电流入信号 并输出相应的电压信号.
其拓扑图为:
- 输入端并联
- 输出端并联
因此被称为 并联-并联反馈 .
由于输入为电流信号, 采样为电压信号, 其也被称为 电流混合电压采样拓扑结构 .
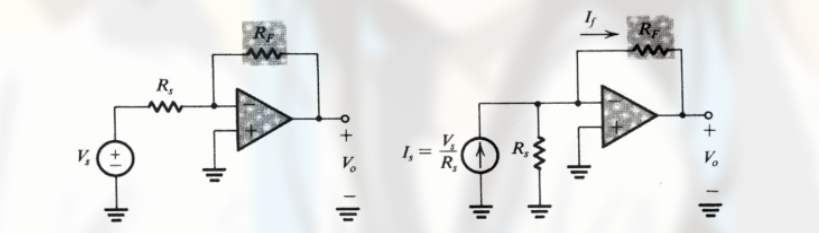
示例, 反相运算放大器:
8.4 串联-并联反馈放大器
8.4.1 理想情况
理想结构如:
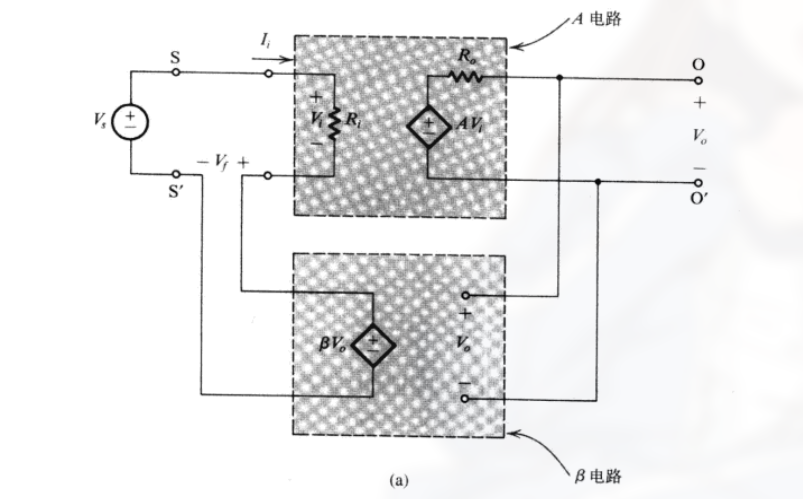
其包含:
- 一个单向化的开环放大器 (上边的方框)
- 一个理想化的电压混合采样反馈网络 (下边的方框)
此时, 闭环增益 $A_f$ 可表示为:
$$
\displaylines
{
\begin{aligned}
A_f = \frac{V_O}{V_S} = \frac{A}{1 + A \beta}
\end{aligned}
}
$$
此串联-并联反馈放大器的等效电路为:
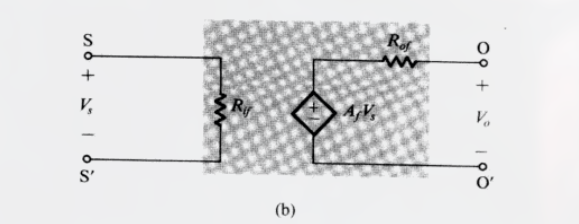
计算输入电阻
有:
$$
\displaylines
{
\begin{aligned}
R_{if} = \frac{V_s}{I_i} = \frac{V_s}{V_i / R_i} \newline~ \newline
= R_i \frac{V_s}{V_i} = R_i \frac{V_i + \neta A V_i}{V_i} \newline~ \newline
R_{if} = R_i (1 + A \beta)
\end{aligned}
}
$$
(其中 $R_{if}$ 为反馈的输入电阻, $R_{of}$ 为反馈的输出电阻)
得出, 该结构的负反馈 将输入电阻增大了与反馈深度相等的倍数
计算输出电阻
令 $V_s = 0$, 并在输出端施加测试电压 $V_t$, 如:
这里:
$$
\displaylines
{
\begin{aligned}
R_{of} = \frac{V_t}{I} \newline~ \newline
I = \frac{V_t - A V_i}{R_O} \newline~ \newline
V_i = -V_f = -\beta V_O = -\beta V_t \newline~ \newline
I = \frac{V_t + A \beta V_t}{R_O} \newline~ \newline
R_{of} = \frac{R_O}{1 + A\beta}
\end{aligned}
}
$$
得出, 该结构的负反馈 将输出电阻减小了与反馈深度相等的倍数
8.4.2 实际情况
反馈网络会引起基本放大器的 负载效应 , 影响 $A$, $R_i$ 和 $R_O$ 的值. 源电阻和负载电阻也会对其造成影响.
8.5 串联-串联反馈放大器
8.5.1 理想情况
理想结构为:
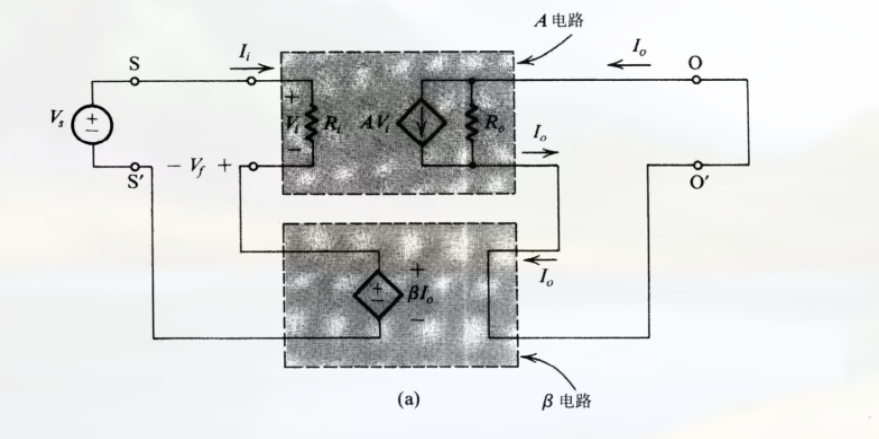
(注意放大器部分和反馈网络部分)
其作用为:
- 稳定 $\frac{I_O}{V_s}$, 用作互导放大器
第10章 频率响应 (英文原版)
放大器所工作的频段, 这里称为 middle-frequency band 或者 midband, 如:
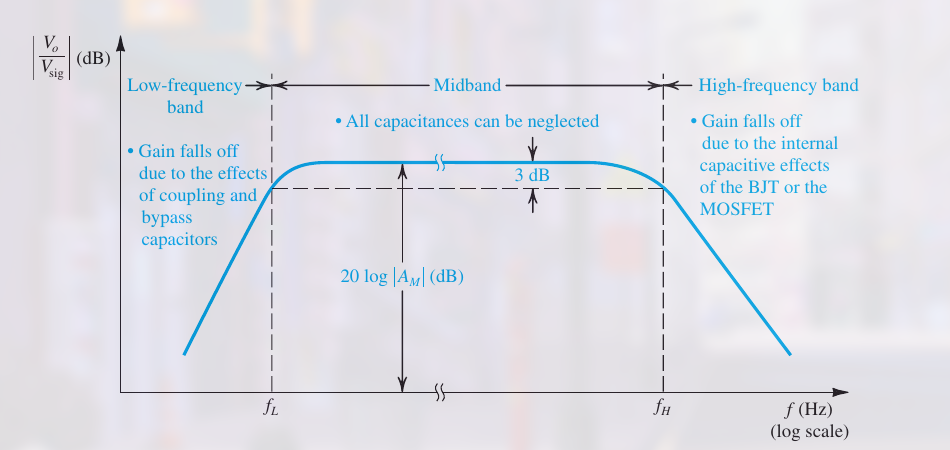
这里是带通滤波器.
如果不是工作在这个频段, 就会失真.
Lower end of the midband 写作 $f_L$. 一般表示低频段 gain 低于 $3dB$ 的部分.
Upper end of the midband 写作 $f_H$. 表示高频段 gain 低于 $3dB$ 的部分.
因此, 放大器的带宽为:
$$
\displaylines
{
\begin{aligned}
BW = f_H - f_L (discrete-circuit amplifiers) \newline~ \newline
BW = f_H (integrated-circuit amplifiers)
\end{aligned}
}
$$
(这里的 BW 指 Band Width)
定义 gain-bandwidth product 为:
$$
\displaylines
{
\begin{aligned}
GB = \left\vert A_M \right\vert BW
\end{aligned}
}
$$
这一章通过增加一些特殊的 circuit components 来增大 amplifier bandwidth.
STC 指 single-time-constant circuits.
10.1 分立 Common-Source 和 Common-Emitter 放大器的低频响应
考虑耦合电容和旁路电容的作用.
什么是 耦合电容
耦合电容指的是将两个电路元件通过电容连接起来,实现信号的传递和耦合的过程中所使用的电容器。在电路中,耦合电容常用于将信号从一个电路传递到另一个电路中,以实现信号的耦合和传递。
在这里,“耦合”一词是指将两个或多个电路元件连接起来,使它们之间相互作用、互相影响的过程。通过耦合电容,两个电路的信号可以相互影响,从而实现信息的传递。这种相互影响的方式可以是电容器中的电荷和电场的相互作用,也可以是电路中的电流和电压的相互作用。
10.1.1 CS 放大器
如:
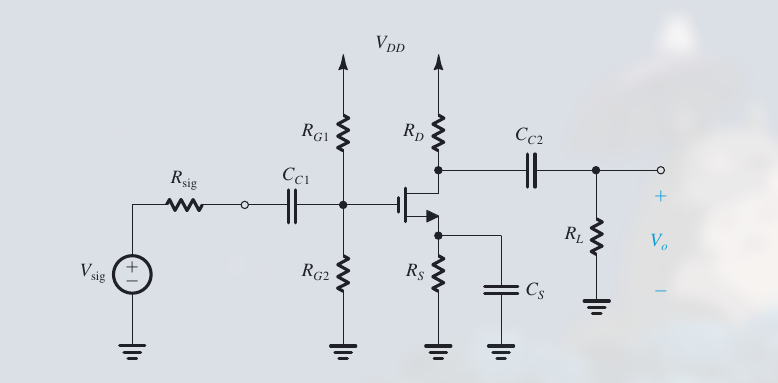
由:
$$
\displaylines
{
\begin{aligned}
Z = \frac{1}{j \omega C}
\end{aligned}
}
$$
可知, 电容 C 越大, 阻抗 Z 越小, 以形成短路 (对于交流输入信号而言)
当输入信号频率很低时, 阻抗会增大, 导致放大器的 gain 减小.
为了计算低频段的 amplifier gain $V_o/V_{sig}$, 将上述电路图转换为:
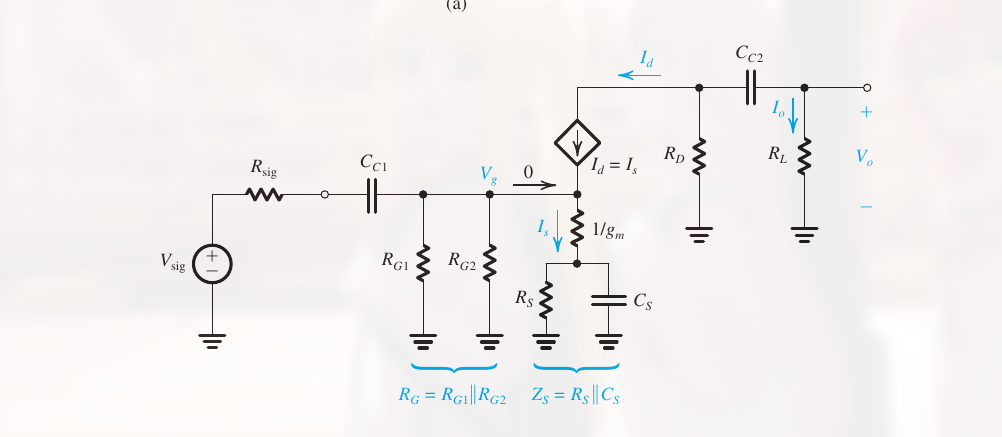
其将 $V_{DD}$ 短路, 且用 T 模型代替 MOSFET.
注意, $r_o$ 在分立元件 amplifier 中是可以被忽略的.
其 gain 可以计算为:
$$
\displaylines
{
\begin{aligned}
\frac{V_O}{V_{sig}} = \frac{V_g}{V_{sig}} \times \frac{I_d}{V_g} \times \frac{V_O}{I_d}
\end{aligned}
}
$$
( $V_g$ 为 gate 和 ground 之间的电压, $I_d$ 是漏极电流 )
计算 $V_g$
$V_g$ 可以通过 $R_{G1}$ 和 $R_{G2}$ 的并联电路电压得到:
$$
\displaylines
{
\begin{aligned}
V_g = V_{sig} \frac{R_G}{R_G + \frac{1}{s C_{C1}} + R_{sig}} \newline~ \newline
即: \newline~ \newline
\frac{V_g}{V_{sig}} = \frac{R_G}{R_G + R_{sig}} \frac{s}{ s + \frac{1}{C_{C1}(R_G + R_{sig})} }
\end{aligned}
}
$$
( 这里是用频域的计算 )
计算截止频率 $\omega_o$
$$
\displaylines
{
\begin{aligned}
\omega_{P1} = \omega_o = \frac{1}{C_{C1}(R_{sig} + R_G}
\end{aligned}
}
$$
其考虑一阶高通滤波器:
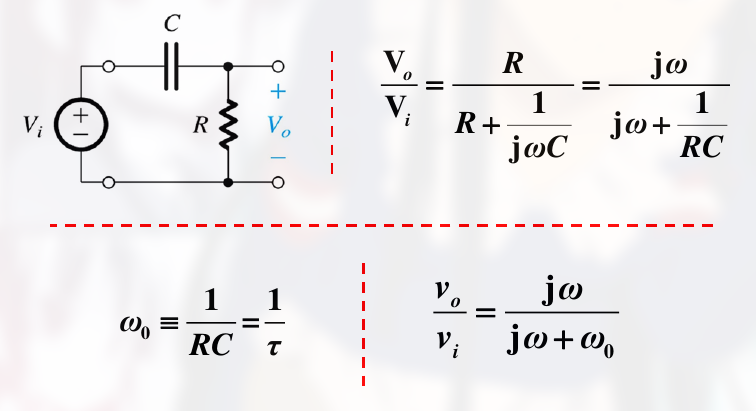
计算 $I_d$
$$
\displaylines
{
\begin{aligned}
I_d = I_s = \frac{V_g}{ \frac{1}{g_m} + Z_S} = g_m V_g \frac{Y_S}{g_m + Y_S} \newline~ \newline
( 分母 \frac{1}{g_m} + Z_S 是总阻抗 ) \newline~ \newline
且有: \newline~ \newline
Y_S = \frac{1}{Z_S} = \frac{1}{R_S} + sC_S \newline~ \newline
因此: \newline~ \newline
\frac{I_d}{V_g} = g_m \frac{s + \frac{1}{C_S R_S}}{ s + \frac{g_m + 1/R_S}{C_S} }
\end{aligned}
}
$$
由此通过旁路电容 $C_S$ 得到第二个截止频率 $\omega_{P2}$ 为:
$$
\displaylines
{
\begin{aligned}
\omega_{P2} = \frac{g_m + 1/R_S}{C_S}
\end{aligned}
}
$$
且有 transmission zero:
$$
\displaylines
{
\begin{aligned}
\omega_Z = \frac{1}{C_S R_S}
\end{aligned}
}
$$
最终得到输出电流为:
$$
\displaylines
{
\begin{aligned}
I_O = - I_d \frac{R_D}{R_D + \frac{1}{sC_{C2}} + R_L}
\end{aligned}
}
$$
可以看出是并联分流来计算的:
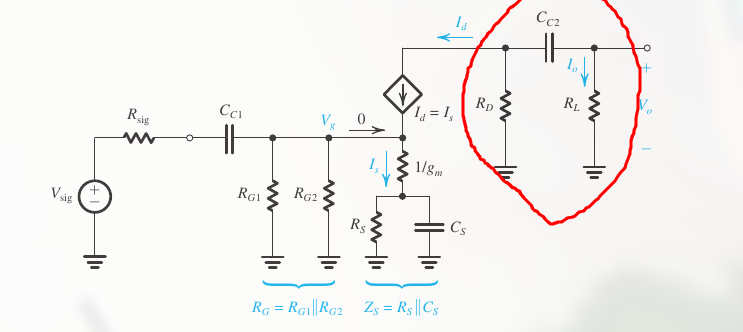
两边同时乘以 $R_L$ 后化简可得 ( $I_O R_L = V_O$ ):
$$
\displaylines
{
\begin{aligned}
\frac{V_O}{I_d} = - \frac{R_D R_L}{R_D + R_L} \frac{s}{s + \frac{1}{C_{C2}(R_D + R_L)}}
\end{aligned}
}
$$
可以计算出 $C_{C2}$ 的截止频率为:
$$
\displaylines
{
\begin{aligned}
\omega_{P3} = \frac{1}{C_{C2} (R_D + R_L)}
\end{aligned}
}
$$
计算增益
$$
\displaylines
{
\begin{aligned}
\frac{V_O}{V_{sig}} = - \frac{R_G}{R_G + R_{sig}} g_m (R_D || R_L) ( \frac{j \omega}{j \omega + \omega_{P1}} )( \frac{\omega_z + j \omega}{j \omega + \omega_{P2}} )( \frac{j \omega}{j \omega + \omega_{P3}} ) \newline~ \newline
= A_M ( \frac{j \omega}{j \omega + \omega_{P1}} )( \frac{\omega_z + j \omega}{j \omega + \omega_{P2}} )( \frac{j \omega}{j \omega + \omega_{P3}} ) \newline~ \newline
其中: \newline~ \newline
A_M = - \frac{R_G}{R_G + R_{sig}} g_m (R_D || R_L)
\end{aligned}
}
$$

10.1.2 短路时间常数方法
一个简单的求解 $f_L$ 的方法:
- 令 $V_{sig} = 0$
- 一次考虑一个电容 $C_i$, 即视其他电容为短路
- 对每一个 $C_i$, 找到总电阻 $R_i$ (不是很懂)
- 计算 3-dB frequency $f_L$:
$$
\displaylines
{
\begin{aligned}
f_L = \sum_{i=1}^n \frac{1}{C_i R_i}
\end{aligned}
}
$$
( n 为电容的数量 )
可以看出, 电容的时间常数越小, $f_L$ 的值越大.
10.2 MOSFET 内部电容效应和高频模型
耦合电容和旁路电容能使 transistor amplifiers 的增益 fall off at the low-frequency end.
transistor 的内部电容效应能使增益 falloff at high frequencies.
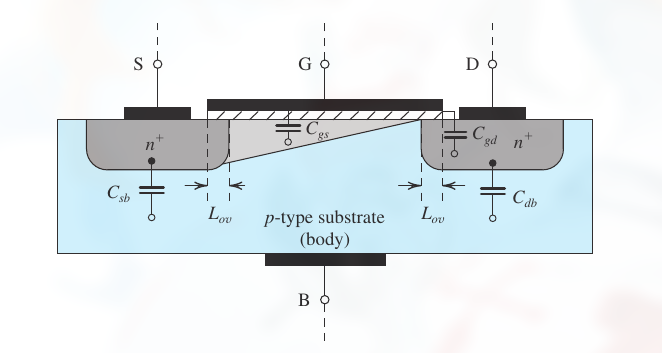
可以看出, MOSFET 内部的四个电容:
- $C_{gs}$ 和 $C_{gd}$ 由 gate-capacitance 效应引起
- $C_{sb}$ 和 $C_{db}$ 是 pn 结的耗尽电容, 由源极和基极, 漏极和基极构成
考虑这些电容时, MOSFET amplifier 的增益会受到频率的影响. 事实上, 在高频时, MOSFET amplifier 的增益就会 fall off.
下图中:

gate capacitance 是以 gate 和 body 的金属板作为两极, 氧化层作为电介质. 其电容的计算为:
$$
\displaylines
{
\begin{aligned}
C_{gs} = WLC_{OX}
\end{aligned}
}
$$
当通道 pinched off 时, 电容变为 $\frac{2}{3}WLC_{OX}$
除这个电容以外, 还有两个电容由于:
- gate 和 source region 的重叠
- gate 和 drain region 的重叠
而形成. 重叠部分长度为 $L_{OV}$ (见图)
计算 $C_{gs}$ 和 $C_{gd}$
因此 gate-to-source capacitance $C_{gs}$ 为:
$$
\displaylines
{
\begin{aligned}
C_{gs} = \frac{2}{3}WL C_{ox} + C_{ov}
\end{aligned}
}
$$
gate-to-drain capacitance $C_{gd}$ 为:
$$
\displaylines
{
\begin{aligned}
C_{gd} = C_{ov}
\end{aligned}
}
$$
计算 $C_{sb}$ 和 $C_{db}$
source-body capacitance, $C_{sb}$ 为:
$$
\displaylines
{
\begin{aligned}
C_{sb} = \frac{C_{sb0}}{ sqrt{1 + \frac{V_{SB}}{V_0}} }
\end{aligned}
}
$$
drain-body capacitance, $C_{db}$ 为:
$$
\displaylines
{
\begin{aligned}
C_{db} = \frac{C_{db0}}{ sqrt{1 + \frac{V_{DB}}{V_0}} }
\end{aligned}
}
$$
MOFET 高频模型
包含四个电容的 MOSFET 小信号模型为:
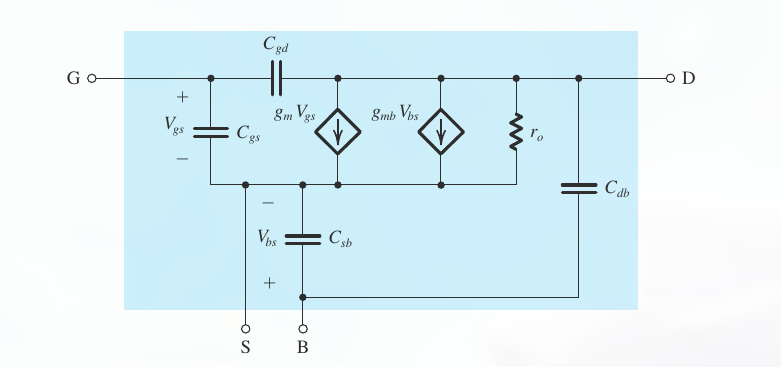
当源极和基极相连时, $C_{sb} = 0$, 且 $C_{db}$ 常被忽略.
因此电路可以简化为:
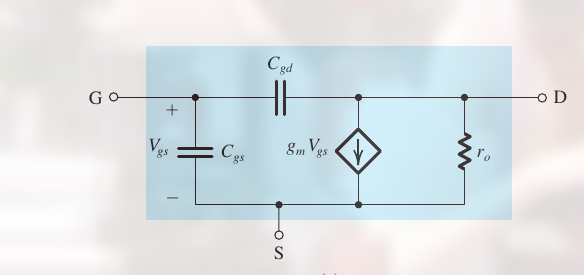
其被称为 MOSFET hybrid-π model.
用 T 模型进行变换可以得到:
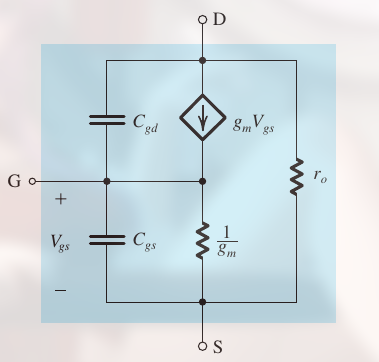
这里定义一个量 The transition frequency $f_T$, 也被称为 MOSFET Unity-Gain Frequency :
- 晶体管在共源电路中的短路电流增益等于1时的频率
通俗来说,当晶体管的转移频率达到一定值时,它的工作状态由放大器转变为开关。在转移频率以下,晶体管的工作状态为放大器,在转移频率以上,晶体管的工作状态为开关
由:
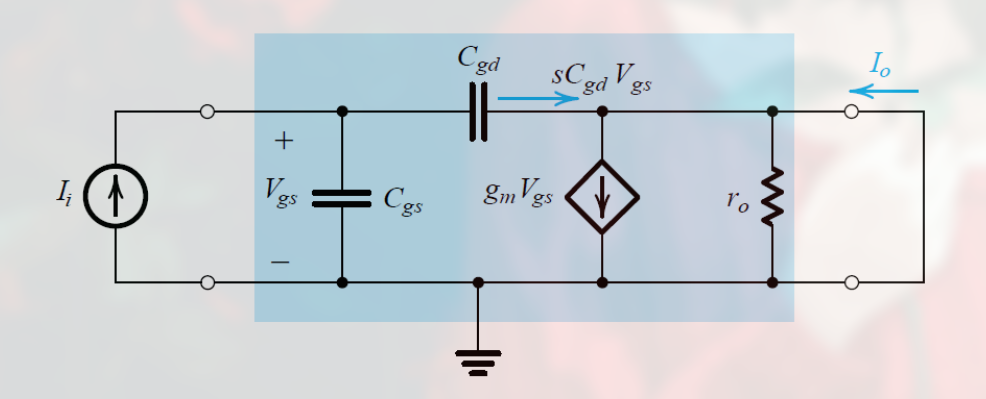
可以得到:
$$
\displaylines
{
\begin{aligned}
I_O = g_m V_{gs} - j\omega C_{gd} V_{gs} \approx g_m V_{gs} \newline~ \newline
V_{gs} = \frac{I_i}{j \omega (C_{gs} + C_{gd})} \newline~ \newline
\frac{I_O}{I_i} = \frac{g_m}{j\omega(C_{gs} + C_{gd})} \newline~ \newline
(也就是短路电流增益) \newline~ \newline
f_T = \frac{g_m}{2\pi (C_{gs} + C_{gd})}
\end{aligned}
}
$$
10.3 CS 放大器的高频响应
Common Source amplifier 的高频等效电路模型为:
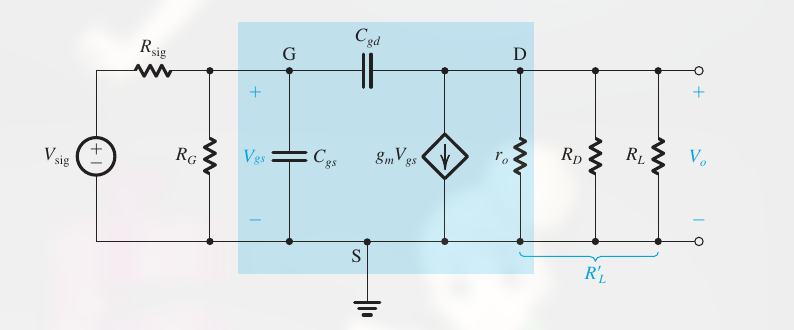
对其输入端应用戴维南定理, 将输出端的电阻合并, 可以得到:
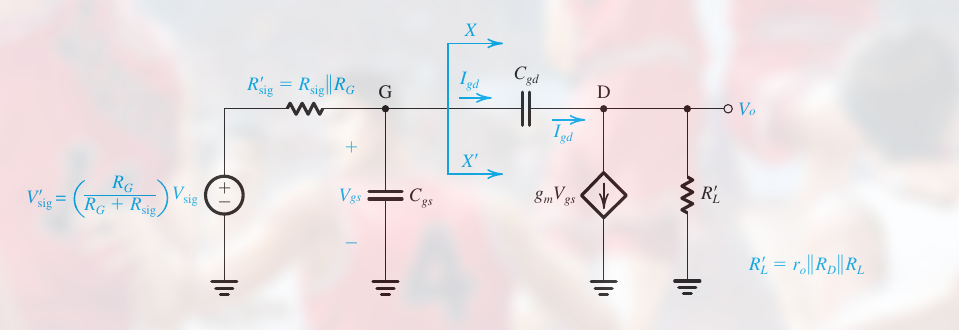
将 $C_{gs}$ 和 $C_{gd}$ 置零, 可以计算出 midband gain $A_M$ :
$$
\displaylines
{
\begin{aligned}
A_M = \frac{V_O}{V_{sig}} = - \frac{R_G}{R_G + R_{sig}} (g_m R_L^\prime)
\end{aligned}
}
$$
为了简化电路, 将 $C_{gd}$ 用等效电容 $C_{eq}$ 代替:
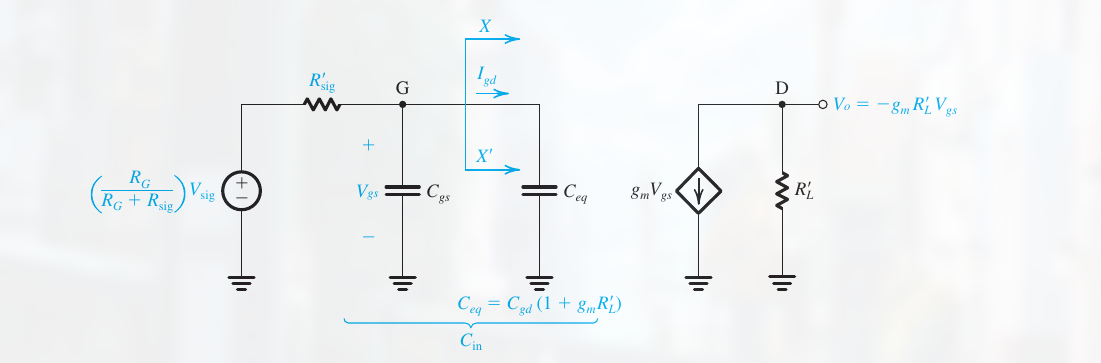
可以求出 负载电流 为:
$$
\displaylines
{
\begin{aligned}
g_m V_{gs} - I_{gd}
\end{aligned}
}
$$
( $g_m V_{gs}$ 是晶体管的输出电流, $I_{gd}$ 是经过 $C_{gd}$ 的微小电流 )
考虑 $I_{gd} \ll g_m V_{gs}$, 则 $V_O$ 可以估算为:
$$
\displaylines
{
\begin{aligned}
V_O \approx -(g_m V_{gs})R_L^\prime = -g_m R_L^\prime V_{gs}
\end{aligned}
}
$$
其中:
$$
\displaylines
{
\begin{aligned}
R_L^\prime = r_o || R_D || R_L
\end{aligned}
}
$$
计算 $I_{gd}$
$$
\displaylines
{
\begin{aligned}
\because V_{O} = V_{ds} \newline~ \newline
I_{gd} = s C_{gd} (V_{gs} - V_O) \newline~ \newline
= s C_{gd}[ V_{gs} - (-g_m R_L^\prime V_{gs}) ] \newline~ \newline
= sC_{gd} (1 + g_m R_L^\prime) V_{gs}
\end{aligned}
}
$$
用 $C_{eq}$ 替换 $C_{gd}$ 的等式
$$
\displaylines
{
\begin{aligned}
sC_{eq} V_{gs} = sC_{gd} (1 + g_m R_L^\prime) V_{gs} \newline~ \newline
C_{eq} = C_{gd} ( 1 + g_m R_L^\prime )
\end{aligned}
}
$$
这里 $C_{eq}$ 比 $C_{gd}$ 大, 被称为 Miller effect , 而 $(1 + g_m R_L^\prime)$ 被称为 Miller multiplier .
下图也被称为 single-time-constant (STC) circuit

其输出电压 $V_{gs}$ 可以计算为:
$$
\displaylines
{
\begin{aligned}
V_{gs} = ( \frac{R_G}{R_G + R_{sig}}V_{sig} ) \frac{1}{1 + \frac{s}{\omega_0}}
\end{aligned}
}
$$
其中 $\omega_0$ 是截止频率 (或 pole frequency):
$$
\displaylines
{
\begin{aligned}
\omega_0 = \frac{1}{C_{in} R_{sig}^\prime}
\end{aligned}
}
$$
有:
$$
\displaylines
{
\begin{aligned}
C_{in} = C_{gs} + C_{eq} = C_{gs} + C_{gd}(1 + g_m R_L^\prime) \newline~ \newline
R_{sig}^\prime = R_{sig} || R_G
\end{aligned}
}
$$
结合:
$$
\displaylines
{
\begin{aligned}
\begin{cases}
V_O \approx -(g_m V_{gs})R_L^\prime = -g_m R_L^\prime V_{gs} \newline~ \newline
V_{gs} = ( \frac{R_G}{R_G + R_{sig}}V_{sig} ) \frac{1}{1 + \frac{s}{\omega_0}}
\end{cases}
\end{aligned}
}
$$
可以得到:
$$
\displaylines
{
\begin{aligned}
\frac{V_O}{V_{sig}} = -( \frac{R_G}{R_G + R_{sig}} ) (g_m R_L^\prime) \frac{1}{1 + \frac{s}{\omega_0}} \newline~ \newline
= \frac{A_M}{1 + \frac{s}{\omega_H}}
\end{aligned}
}
$$
其中, $\omega_H$ 为 upper 3-dB frequency:
$$
\displaylines
{
\begin{aligned}
\omega_H = \omega_0 = \frac{1}{C_{in}R_{sig}^\prime} \newline~ \newline
f_H = \frac{\omega_H}{2 \pi} = \frac{1}{2\pi C_{in} R_{sig}^\prime}
\end{aligned}
}
$$
