傅里叶级数理解

知乎文章

0 频率也被称为直流分量, 在傅里叶级数的叠加中, 其仅仅影响全波形相对于数轴整体向上或是向下而不改变博得形状.

正弦函数的定义

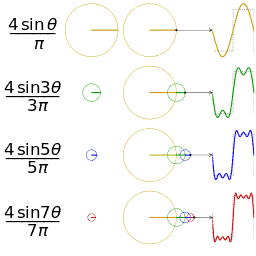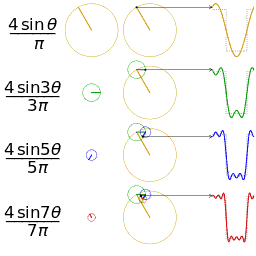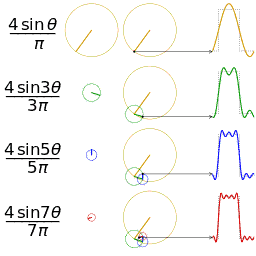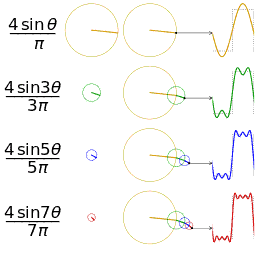
频域图像理解

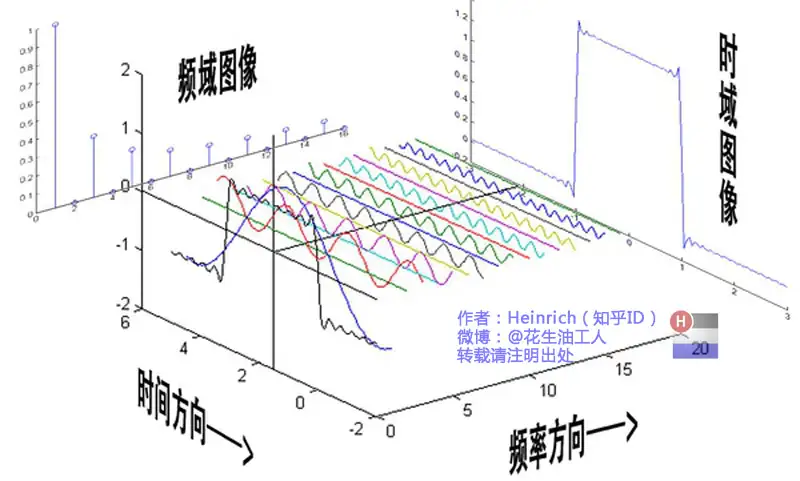
频谱包含振幅信息, 还需要相位谱, 包含相位信息:

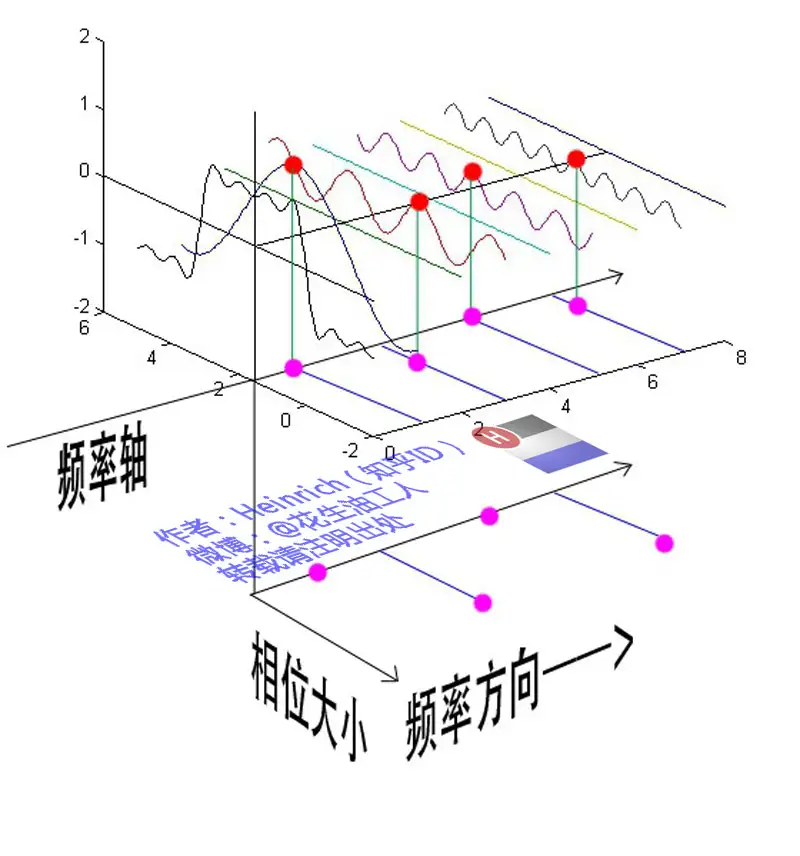
可以整合为:

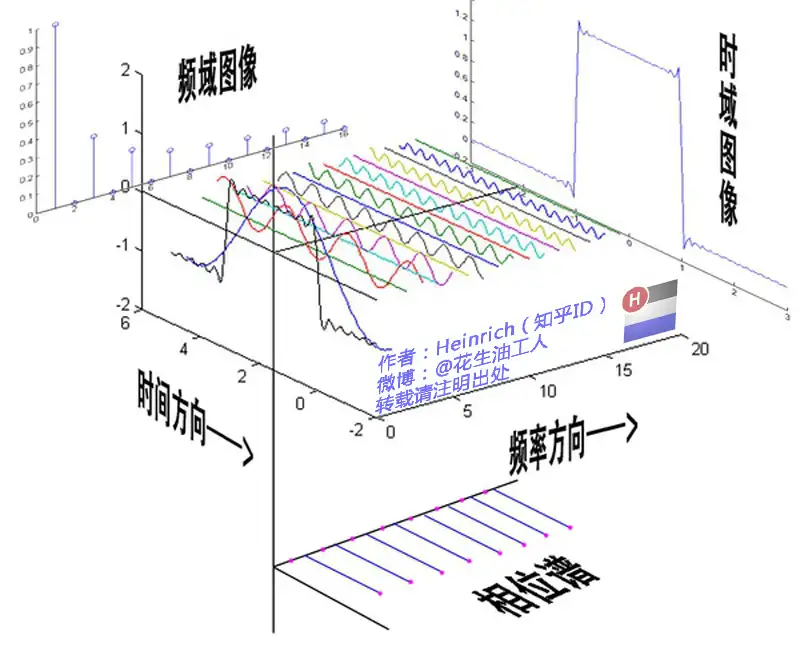
为什么需要傅里叶分析

很多在时域不方便的操作, 在频域下很方便. 如滤波, 微分和积分运算.

傅里叶级数

傅里叶级数的本质是将一个周期的信号分解成无限多分开的（离散的）正弦波.

傅里叶变换

傅里叶变换，则是将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号.

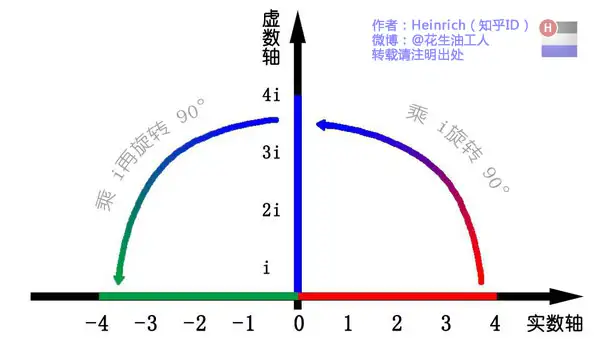
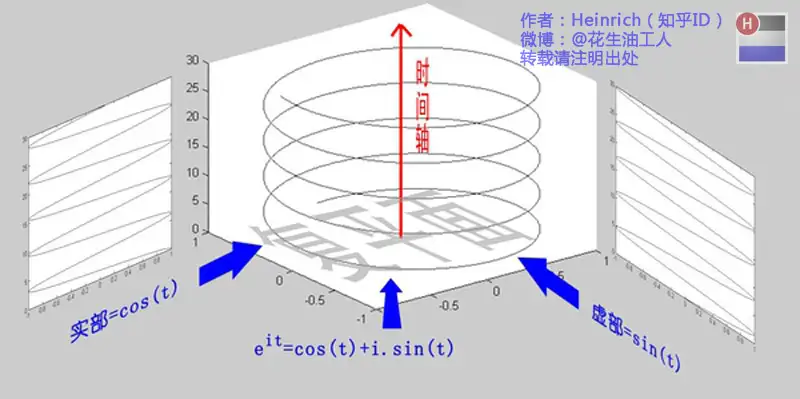
欧拉公式

对虚数 i 的理解:

$$
\displaylines
{
\begin{aligned}
e^{ix} = cosx = isinx
\end{aligned}
}
$$