Structure-and-Interpretation-of-Computer-Programs-Notes

教材答案

1 用 Procedures 构建 Abstractions

Lisp 是 LISt Processing 的缩写.

1.1 The Elements of Programming

Lisp 的 prefix notation 可以方便获取 arbitrary number of arguments, 如:

1
(+ 21 35 12 7)

另一个好处为便于嵌套组合:

1
(+ (* 3 5) (- 10 6))

pretty-printing:

1
2
3
4
(+ (* 3
      (+ (* 2 4)))
   (+ (- 10 7)
      6))

1.1.2 名称和环境

Lisp 中用 define 来命名, 如:

1
2
3
4
(define size   2)
(define radius 10)
(define pi     3.14159)
(define calc (* pi radius size))

environment

为了让 value 和一个 symbols 联系起来, interpreter 需要用一段内存 keeps track of the name-object pairs, 而这段内存就被称为 environment.

1.1.3 Evaluating Combinations

为了计算一个 combinations, interpreter 需要先确定 subexpressions of the combination 的值, 这种计算过程则是 recursive.

下列 process:

1
2
(* (+ 2 (* 4 6))
   (+ 3 5 7))

可以描述为:

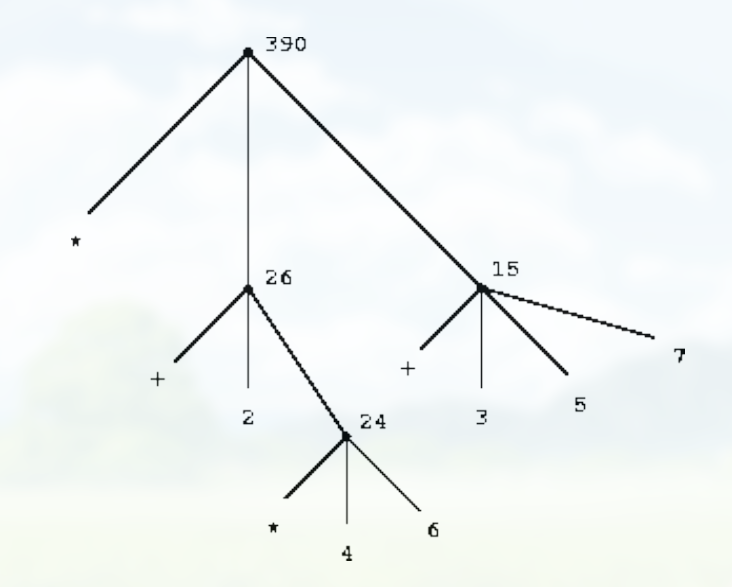
(tree-accumulation 表示)

不产生分支的 nodes 被称为 terminal nodes.

1.1.4 Compound Procedures

procedure definition

形式为:

1
(define (<name> <formal parameters>) <body>)

如:

1
(define (square x) (* x x))

normal-order evaluation 和 applicative-order evaluation

这两个为不同的求值策略 (即表达式中的字表达式什么时候被求值)

normal-order evaluation, 先将表达式完全展开为最简形式, 然后求值, 如:

1
2
3
4
5
(define (square x)
  (* x x))

(define (example a b)
  (+ (square a) b))

当计算 (example 3 4) 时, 先进行展开:

1. 

1
(+ (square 3) 4)
  1. 1
    (+ (* 3 3) 4)

最后求值:

1
2
(+ 9 4)
13

而 applicative-order 先对参数 (子表达式求值), 然后计算出结果, 如求 (example 3 4):
1.

1
2
(square 3)
4
  1. 1
    2
    (+ 9 4)
    13

Lisp 采用的为 applicative-order, 其性能会略高.

1.1.6 条件表达式和 Predicates

Lisp 中的条件语句用 cond (Conditional)

如:

1
2
3
4
(define (abs x)
  (cond
    ((< x 0) (-x))
    (else x)))

类似 (> x 0) 这种就被称为 predicates.

if 语句

形式为:

1
2
3
(if condition
    then-expression
    else-expression)

如:

1
2
3
4
(define (abs x)
    (if (< x 0)
        (-x)
        x))

同样可用 and, or, not

如:

1
2
3
4
5
(and (> x 5) (< x 10))

(or (> x 5) (< x 10))

(not (< x 10))

1.1.7 用牛顿法求平方根

牛顿法介绍

先简单看下牛顿法的解法.

Newton method 是一种用于寻找方程的数值近似解的迭代算法 (也就是用来解方程), 其基本思想是从一个初始猜测的解开始，通过不断改进的迭代过程，逐渐接近方程的真实解。具体步骤如下：

  1. 选择一个初始猜测值（通常是方程的一个近似解）作为起点。

  2. 在当前猜测值处，计算方程的函数值和导数值。函数值表示方程与当前猜测值的差距，导数值表示方程的斜率。

  3. 使用当前猜测值和函数值、导数值的信息，通过牛顿迭代公式进行迭代计算，得到下一个猜测值。

  4. 重复步骤2和步骤3，直到达到预设的停止条件（例如，达到预设的精度要求或迭代次数）

如:

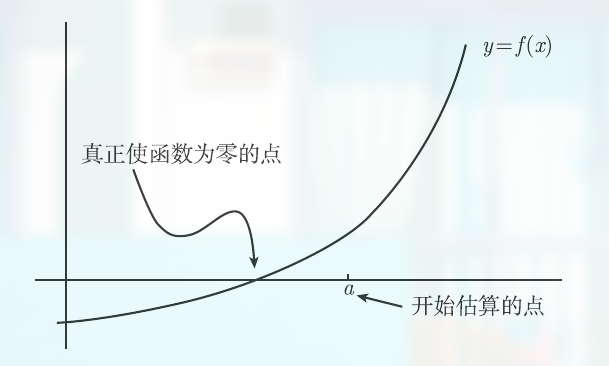
接着通过 f 在 x=a 处的线性化来改善估算:

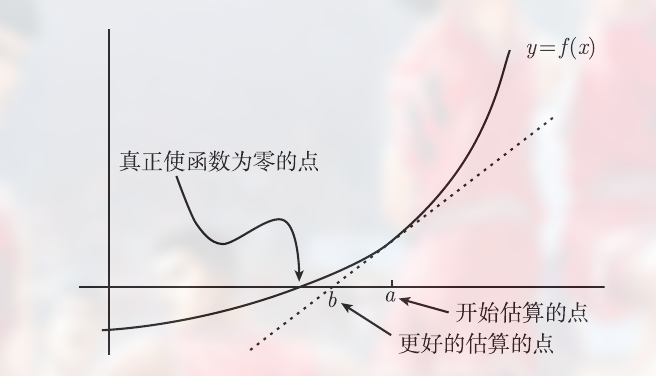
此时 b 的值为:

$$
\displaylines
{
\begin{aligned}
L(x) = f(a) + f’(a)(x-a)
\end{aligned}
}
$$
在 x 轴的截距.

可以解出:
$$
\displaylines
{
\begin{aligned}
x = a - \frac{f(a)}{f’(a)}
\end{aligned}
}
$$

因此得到的牛顿法的公式为:
$$
\displaylines
{
\begin{aligned}
b = a - \frac{f(a)}{f’(a)}
\end{aligned}
}
$$

之后就是不断迭代, 求出最优解.

在有些情况下牛顿法会不起作用:

  • f'(a) 的值接近于 0
  • f(x) = 0 有不止一个解
  • 用牛顿法时, 近似越来越糟糕或循环.

Lisp 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(define (average x y)
  (/ (+ x y) 2))

(define (improve guess x)
  (average guess (/ x guess)))

(define (good-enough? guess x)
  (< (abs (- (* guess guess) x)) 0.001))

(define (sqrt-iter guess x)
  (if (good-enough? guess x)
    guess
    (sqrt-iter (improve guess x)
               x)))

(define (sqrt x)
  (sqrt-iter 1.0 x))

(display (sqrt 15))

1.2 Procedures and the Processes They Generate

1.2.1 Linear Recursion and Iteration

以 deferred operation 进行收缩的过程即 recursive process, 编译器需要记录以后会执行的操作.

Iteration 的状态可以用一系列 iterative evariables 表示. Iteration 操作维护一组变量. 其关键特点是, 在递归调用之前不会有其他操作或表达式需要执行. 这使得编译器或解释器可以对尾递归进行优化, 以避免创建额外的函数调用栈帧 (函数的执行环境).相反, 它可以重用当前函数的调用栈帧, 从而节省内存空间, 并使递归函数的执行效率更高.

Lisp
Structure-and-Interpretation-of-Computer-Programs-Notes
http://example.com/2023/10/29/Structure-and-Interpretation-of-Computer-Programs-Notes/
作者
Jie
发布于
2023年10月29日
许可协议