数据结构与算法基础知识
算法的定义
算法 (Algorithm) 是对特定问题的求解方法和步骤的一种描述, 是指令的有限序列, 其中每个指令表示一个或多个操作.
对于同一个问题, 使用不同的算法, 所消耗的资源也是不同的, 这里的资源指时间和空间:
- 时间维度, 指执行当前算法所消耗的时间, 通常用 “时间复杂度” 来描述
- 空间维度, 是指执行当前算法需要占用多少内存空间, 通常用 “空间复杂度” 来描述
大O表示法
大O表示法是一种用于描述算法时间复杂度和空间复杂度的数学符号. 它表示的是算法在最坏情况下的性能.
如:
1 | |
T(n), 表示算法在处理规模为 n (n 随数据结构不同而含义不同, 如图结构, n 表示顶点数或边数) 的输入时所需要的时间 (或步骤数)f(n)是一个函数, 这里描述T(n)的增长速度O(f(n))表示函数f(n)的上界 (似乎是表示f(n)的正比例函数)
具体说, 当 n 趋于无穷大时, T(n) 的增长速度不会超过 f(n) 的常数倍.
为什么说描述的是一个增长速度?
因为始终考虑的是 f(n) 这一函数, 而非 n 这个值.
数学定义
要找到 f(n), 需要知道: T(n) = O(f(n)) 意味着存在常数 c 和 n0, 使得对于所有 $n \ge n_0$, 都有:
$$
\displaylines
{
\begin{aligned}
T(n) \le c \cdot f(n)
\end{aligned}
}
$$
理解
使用大O表示法, 就是找到一个函数 f(n), 用其正比例值来描述算法的复杂度.
例子1: 线性时间复杂度
假设有:
$$
\displaylines
{
\begin{aligned}
T(n) = 3n + 2
\end{aligned}
}
$$
用大O表示其复杂度:
$$
\displaylines
{
\begin{aligned}
\because 能找到常数 c 和 n_0,使得对于所有的n \ge n_0 都有 \newline~ \newline
3n + 2 \le c \cdot n \newline~ \newline
比如取 c=4: \newline~ \newline
3n+2 \le 4n, 当 n \ge 1 时成立
\end{aligned}
}
$$
因此可以表示为 O(n).
例子2: 平方复杂度
假设有:
$$
\displaylines
{
\begin{aligned}
T(n) = 2n^2 + 3n + 1
\end{aligned}
}
$$
用大O表示其复杂度:
$$
\displaylines
{
\begin{aligned}
\because 能找到常数 c 和 n_0,使得对于所有的n \ge n_0 都有 \newline~ \newline
2n^2 + 3n + 1 \le c \cdot n^2 \newline~ \newline
比如取 c=3, n_0=1: \newline~ \newline
2n^2 + 3n + 1 \le 3n^2, 当 n \ge 1 时成立
\end{aligned}
}
$$
因此可以表示为 O(n^2).
常见的时间复杂度:
常数阶,
O(1)
常数时间复杂度表示算法的执行时间与输入规模无关, 无论输入规模多大, 执行时间始终是常数:1
2
3
4
5
6
7def constant_time_example(arr):
# 只访问第一个元素,时间复杂度为 O(1)
return arr[0]
# 示例使用
arr = [1, 2, 3, 4, 5]
print(constant_time_example(arr)) # 输出: 1线性阶,
O(n)
线性时间复杂度表示算法的执行时间与输入规模成正比:1
2
3
4
5
6
7
8
9
10def linear_time_example(arr):
# 遍历整个数组,时间复杂度为 O(n)
total = 0
for num in arr:
total += num
return total
# 示例使用
arr = [1, 2, 3, 4, 5]
print(linear_time_example(arr)) # 输出: 15平方阶,
O(n^2)
平方时间复杂度表示算法的执行时间与输入规模的平方成正比:1
2
3
4
5
6
7
8
9
10
11
12
13def quadratic_time_example(arr):
# 嵌套循环,时间复杂度为 O(n^2)
n = len(arr)
pairs = []
for i in range(n):
for j in range(n):
pairs.append((arr[i], arr[j]))
return pairs
# 示例使用
arr = [1, 2, 3]
print(quadratic_time_example(arr))
# 输出: [(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]对数阶,
O(logn)
对数时间复杂度表示算法的执行时间与输入规模的对数成正比, 通常出现在分治算法中, 如二分查找 (要遍历的数据量 2 倍 2 倍减少):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def logarithmic_time_example(arr, target):
# 二分查找,时间复杂度为 O(log n)
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
# 示例使用
arr = [1, 2, 3, 4, 5]
print(logarithmic_time_example(arr, 4)) # 输出: 3线性对数阶,
O(nlogn)
线性对数时间复杂度通常出现在高效排序算法中,如归并排序和快速排序:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26def linearithmic_time_example(arr):
# 归并排序,时间复杂度为 O(n log n)
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left_half = linearithmic_time_example(arr[:mid])
right_half = linearithmic_time_example(arr[mid:])
return merge(left_half, right_half)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
# 示例使用
arr = [5, 2, 9, 1, 5, 6]
print(linearithmic_time_example(arr)) # 输出: [1, 2, 5, 5, 6, 9]
在图像上则是:
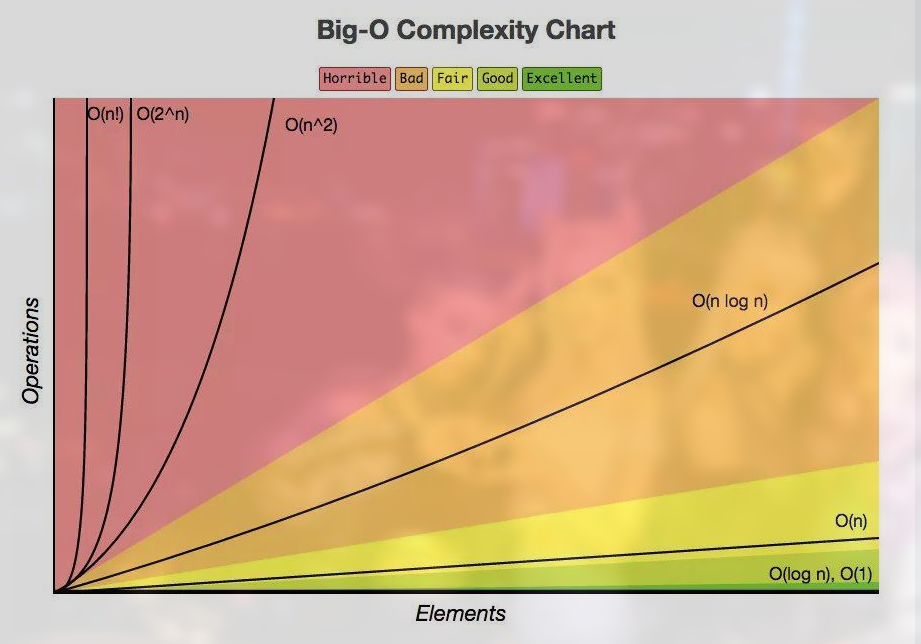
可以看出速度关系为:
1 | |
数据结构
数据结构是一种组织和存储数据的方式, 以便能够高效地访问和修改数据. 数据结构不仅仅是数据的集合, 还包括数据之间的关系以及可以对数据进行的操作.
很多非数值 (比如, 文字, 图像, 声音) 计算问题的数学模型不能用数学方程表示, 而是诸如表, 树和图之类的具有逻辑的数据, 这些就是数据结构.
线性数据结构
线性关系数据结构是指数据元素之间存在一对一的关系, 即每个元素有且仅有一个前驱和一个后继 (除第一个和最后一个元素外). 这些数据结构中的元素排列成一条直线, 如:
- 数组, Array
- 链表, Linked List
- 栈, Stack
- 队列, Queue
非线性关系数据结构
非线性关系数据结构是指数据元素之间存在多对多的关系, 即每个元素可能有多个前驱和多个后继. 这些数据结构中的元素排列成一种层次或网络结构. 如:
- 树, Tree
- 图, Graph